1.Prawo powszechnego ciążenia dla pkt. materialnych (skalarnie i wektorowo)

• Wzajemne przyciąganie się ciał jest źródłem jednej z podstawowych sił w fizyce - sił przyciągania, które podlegają prawu powszechnego ciążenia (grawitacji). Prawo to podał Isaac Newton (1687; pierwsze obserwacje już od 1655)

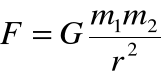
Między każdymi dwoma punktami materialnymi działa siła wzajemnego przyciągania, wprost proporcjonalna do iloczynu mas tych punktów (m₁ i m₂) a odwrotnie proporcjonalna do kwadratu odległości r między nimi.

• W postaci wektorowej prawo to można zapisać, jako:

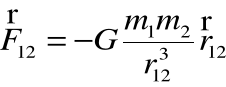
to siła, z jaką punkt „2” działa na punkt „1”,
to promień wodzący, łączący punkt drugi z pierwszym.

• Siła działająca między każdymi pkt. materialnymi o masach m1 i m2 znajdującymi się w odległości r jest siłą przyciągającą skierowaną wzdłuż prostej łączącej te pkt. G jest stałą uniwersalną mającą tę samą wartość dla wszystkich par pkt. materialnych

• Siły grawitacyjne działające między dwoma dowolnymi ciałami (pkt. materialnymi) stanowią parę sił: akcja i reakcja

• Siła graw między danymi dwoma ciałami nie zależy od obecności innych ciał i od właściwości otaczającej te ciała przestrzeni. Zatem nie można zbud ekranu grawitacyjnego ( w przeciwieństwie do pól elektrycz i magnetyczn)

• Masy występujące we wzorach na oddziaływanie grawitacyjne są tymi samymi, jakie odpowiadają za efekt bezwładności ciała ( II zasada dynamiki). Zatem masa grawitacyjna jest równa masie bezwładnej ciała

2. Oddziaływanie grawitacyjne mas rozciągłych w przestrzeni

• Ciało o budowie ciągłej jest szczególnym przykładem ściśle upakowanych pkt. materialnych. Dokonujemy tutaj sumowania ( całkowania po całej masie ciała) oddziaływań grawitacyjnych dF pochodzących od wszystkich upakowanych cząsteczek dm, które traktujemy jak pkt materialne.

• W przypadku dwóch ciał o bud ciągłej należy zsumować oddziaływania miedzy wszystkimi parami pkt obu ciał

(ameba)

• W najbardziej ogólnym przypadku dla ciał o skomplikowanej bud należy oddziaływania graw obliczać metodą całkowanie

• Na ogół nie jest poprawne założenie, że dla celów graw całą masę ciała możemy traktować, jako skoncentrowaną w jego środku masy….

• … wyjątkiem są powłoki i ciała kuliste o jednorodnej gęstości…

• Oddziaływanie graw powłoki kulistej o jednorodnej gęstości na cała znajdujące się poza nią ( lub co najwyżej na jej powierzchni) można zredukować do oddziaływani pkt materialnego o takiej samej masie M umieszczonego w środku masy powłoki Sm.

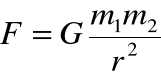
• Oddziaływanie graw powłoki kulistej o jednorodnej gęstości na ciała znajdujące się w jej wnętrzu jest ZEROWE! ( przyczynki oddziaływań od wszystkich elem. Powłoki znoszą się!)

• Oddziaływanie graw kuli o jednorodnej gęstości na ciała znajdujące się poza nią można zredukować do oddziaływania pkt materialnego o takiej samej masie M umieszczonego w ośrodku masy kuli sm. W środku masy Sm pole grawitacyjne jest zerowe ( stan nieważkości), oddziaływanie zewnętrznej powłoki kuli jest zerowe.

3. Natężenie pola grawitacyjnego. Przyśpieszenie ziemskie

• Grawitacje można traktować, jako bezpośrednie oddziaływanie między dwoma ciałami obdarzonymi masą, odmiennym pkt widzenia jest koncepcja pola: ciało obdarzone masą M modyfikuje w pewien sposób otaczającą przestrzeń tworząc tzw. Pole grawitacyjne, które działa na każde inne znajdujące się w nim ciało obdarzone masą, wywierając nań siłę przyciągania grawitacyjnego.

• Pojęcie pola jest niezwykle ważne w fizyce. Ma istotne zalety zarówno pojęciowe jak i praktyczne (umożliwia analizę oddziaływań bez konieczności brania pod uwagę ich źródeł)

• Przy oddziaływaniu dwóch ciał M i m można oczywiście mówić zarówno o polu wyt. Przez ciało M i oddziałującym na m jak i o polu ciała m oddziałującym na M.

gdzie: m - masa ciała; F - siła, jaka działa na ciało.

Natężenie pola grawitacyjnego wytwarzane przez punkt materialny opisuje wzór:

gdzie

r - odległość od punktu materialnego,

M - punktowa masa,

G - stała grawitacyjna.

Wzór ten obowiązuje również, gdy ciało wytwarzające pole grawitacyjne jest jednorodną kulą lub sferą albo ma radialnie symetryczny rozkład gęstości - Ziemia i wszystkie większe ciała niebieskie w przybliżeniu spełniają ten warunek. Wówczas r we wzorze jest odległością od środka kuli. Wzór ten pozostaje prawdziwy na zewnątrz kuli, tzn. dla r > R, gdzie R jest promieniem kuli.

4. Energia potencjalna w polu grawitacyjnym. Potencjał grawitacyjny

• Siły grawitacyjne są siłami zachowawczymi, czyli w obecności działania sił zachowawczych sensowne jest wprowadzenie pojęcia energii potencjalnej.

• Pojęcie potencjału jest niezwykle ważne w teorii pola! Aby uzyskać energię potencjalną Ep ciała m w polu grawitacyjnym wystarczy przemnożyć potencjał pkt. W którym znajduje się ciało przez masę ciała

• Parametry F,g,V pola pochodzącego od ciała o bud ciągłej obliczamy dokonując sumowania (całkowania po całej masie ciała) przyczynków dF,dg,Dv pochodzących od wszystkich upakowanych cząsteczek dm które traktujemy jak pkt materialne

• Wielkości wektorowe F,g należy sumować ( całkować) wektorowo a skalarnie V!

• W przypadku dwóch ciał o bud ciągłej należy zsumować oddziaływania między wszystkimi parami pkt obu ciał

(ameba)

• Zależność między natężeniem pola i potencjałem
  

14. Naładowany przewodnik izolowany o kulistym kształcie (natężenie pola, potencjał pola)

15. Dwa naładowane i połączone przewodniki kuliste o różnych promieniach (potencjały, powierzchniowe gęstości ładunku, natężenia pola),

16. Pojęcie pojemności. Pojemności izolowanej, przewodzącej kuli.

• Jak wiadomo na powierzchni przewodnika można zgromadzić ładunek elektryczny Q, czemu odpowiada stosowana wartość potencjału przewodnika V ( przewodząca kula rys)

• Można zdefiniować pojemność
  

17. Kondensator płaski bez dielektryka

• W technice częściej stosuje się układ przewodników, okładek o powierzchniach S, odległych od siebie o d ( kondensator płaski). Na wewnętrznej (zwróconej ku sobie) powierzchnie okładek można wprowadzić ładunki o równych lecz przeciwnych znakach +Q oraz -Q (ładunki swobodne)

(rys.)

18. Kondensator płaski z dielektrykiem

• (rys.)

• Pojemność kondensatora z dielektrykiem jest
  razy większa od kondensatora próżniowego o tych samych wymiarach.

• Przy wysuwaniu dielektryka do naładowanego i ciągle podłączonego do źródła napięcia kondensatora

• Napięcie V między okładkami maleje
  razy

• Natężenie pola E między okładkami maleje
  razy

• Ładunek Q kondensatora nie zmienia się ponieważ okładki są odłączone od baterii i ładunek nie ma drogi dopływu/odpływu

• Przy wsuwaniu dielektryka do naładowanego i ciągle podłączonego do źródła napięcia kondensatora

• Napięcie V między okładkami nie zmienia się Wymusza je źródło napięcia

• Natężenie pola E między okładkami nie zmienia się ponieważ E=V/d, a napięcie się nie zmienia

• Ładunek Q kondensatora wzrasta
  razy ponieważ wzrasta pojemność kondensatora a napięcie się nie zmienia

• UWAGA powyższe wnioski są ściśle ilościowo tylko wówczas gdy dielektryk wypełnia cały obszar między okładkami kondensatora. W innym przypadku powyższe wnioski są poprawne jakościowo a ścisłe rachunki należy wykonać stosowane do sytuacji ( korzystając z prawa Gaussa)

19. Izolowany przewodnik metaliczny bez zewnętrznego pola elektrycznego

• (rys)

• W odosobnionym przewodniku metalicznym istnieją swobodne elektrony będące w ciągłym ruchu ( podobnie jak cząsteczki gazu w zbiorniku). W miedzi na jeden przypada jeden elektron swobodny ( elektron walencyjny, elektron przewodnictwa) pozostałe 28 elektrony w miedzi związane są z jądrem ( tworząc dodatni rdzeń jonowy w ramach sieci krystalicznej metalu)

• Ilość elektronów swobodnych na jednostkę objętości jest ogromna(ncu=2,2E22 [1/cm3]

• Elektrony przewodnictwa mogą poruszać się swobodnie w sieci rdzeni jonowych są one odpowiedzialne za przewodnictwo elektryczne, ale również za przewodnictwo cieplne

• Średnia termiczna prędkość elektronów przewodnictwa jest bardzo duża (dla miedzi Vcu=1,6E8[cm/s])

• Wzdłuż przewodnika nie występuje średni wypadkowy ruch elektronów

• Z relacji na skończoną ilość elektronów mogą wystąpić drobne fluktuacje ich konfiguracji( szum śrutowy)

20. Izolowany przewodnik metaliczny w zewnętrznym polu elektrycznym

• (rys)

• W izolowanym przewodniku umieszczonym w polu elektrycznym E następuje przegrupowanie części ładunków elektrycznych. W wyniku tego powstaje dodatkowe pole elektryczne E'. Ruch ładunków będzie trwał do momentu, gdy oba pola się skompensują (E+E'=0). W efekcie we wnętrzu przewodnika nie będzie pola elektrycznego.

• Dzięki powyższemu procesowi przewodniki mogą być wykorzystywane w roli ekranów elektrycznych ( to czy przewodnik jest w środku pełny czy pusty nie zmienia sytuacji)

• W stanie stacjonarnym we wnętrzu przewodnika nie może istnieć pole elektryczne!

21. Przewodnik metaliczny z różnicą potencjałów na końcach. Natężenie i gęstość prądu

• (rys.)

• Po przyłożeniu różnicy potencjałów nowa konfiguracja pola elektrycznego rozprzestrzenia się w przewodniku z prędkością światła (rzędu 10E8 m/s)

• Na chaotycznym ruch elektronów przewodnictwa (duża prędkość) nakłada się prędkość unoszenia pod wpływem oddziaływania (mała prędkość np. Vucu=3,6E-2 [cm/s]=1cm/28s!!! (dla średnicy drutu 1,63mm i prądu 10A)

• Istnienie niezerowego pola elektrycznego wewnątrz przewodnika możliwe jest tylko w stanie niestacjonarnym(istnieje wypadkowy ruch ładunków a na końcach przewodnika podtrzymywana jest różnica potencjałów.)

• W sytuacji niestacjonarnej wzdłuż przewodnika następuje zmiana potencjału

• Natężenie prądu i (skalar !)(rys.)

• To stosunek ilości ładunku przepływającego przez dowolny przekrój przewodnika (o powierzchni S) do czasu w którym ten ładunek przepłynął

• 
  

• Gęstość prądu j ( wektor !)(rys.)

• To stosunek natężenia pr. Do powierzchni przez którą ten pr. Przepływa

• 
  

• Zależność między j oraz i

• Dla dowolnej powierzchni, która nie musi być płaszczyzną i jest strumieniem wektora j przez tę powierzchnię

• 
  

• Natężenie pr i jest wielkością makroskopową identyczną dla wszystkich przekrojów poprzecznych danej gałęzi przewodnika

• Gęstość pr j jest wielkością mikroskopową (metale ciecze (elektrolity) gazy (plazma)) nośniki ładunku mogą być różne (elektrony lub inne cząstki elementarne, dziury, jony atomowe i molekularne)

• Większość zewnętrznych skutków wywołanych przez dodatni ładunek poruszający śie w pewnym kierunku, jest równoważne skutkom wywołanym przez ładunek ujemny poruszający się w przeciwnym kierunku. W związku z tym, dla prostoty opisu zakładamy, że wszystkie nośniki ładunku są dodatnie i rysujemy strzałki pr ( oraz wektory gęstości pr) w kierunku, w którym poruszałyby się takie ładunki

• Istnieją wyjątki powyższej reguły (np. zjawisko Halla) i wówczas odrzucamy powyższą umowę i bierzemy pod uwagę aktualną sytuację.

22. Opór przewodników. Przykład przewodnika walcowego.

• 
  (rys.)

• dla przewodnika, walcowego,
  , gdzie:
  - opór właściwy

• opór właściwy
  jest konsekwencją zderzeń nośników ładunku(elektronów) z rdzeniami jonowymi, domieszkami oraz sieci krystalicznej metalu. W konsekwencji zależy on od temperatury( wzrost amplitudy drgań sieci), ilości domieszek (zanieczyszczenia), naprężeń, obróbki cieplnej, itp.

• Wielkość mikroskopowa ma istotne znaczenie kiedy zajmujemy się podstawowymi własnościami materii oraz kiedy interesujemy się właściwościami przedmiotów przewodzących o nieregularnych kształtach.

23.Prawo Ohma w ujęciu makro- i mikro- skopowym

• Jeżeli do przewodnika przyłożymy napięcie U (różnicę potencjałów ΔV), to przez

przewodnik płynie prąd, którego natężenie I jest proporcjonalne do przyłożonego napięcia.

Ten ważny wynik doświadczalny jest treścią prawa Ohma, które stwierdza, że

Stosunek napięcia przyłożonego do przewodnika do natężenia prądu

przepływającego przez ten przewodnik jest stały i nie zależy ani od napięcia ani od

natężenia prądu.

nazywamy oporem elektrycznym .

• Jednostki

Jednostką oporu jest ohm (Ω); 1Ω = 1V/A.

Prawo Ohma jest słuszne pod warunkiem, że przewodnik znajduje się w stałej

temperaturze. Zależność oporu od temperatury jest omówiona w dalszej części.

• W ujęciu makroskopowym ma podstawowe znaczenie, kiedy wykonujemy pomiary elektryczne na konkretnych przedmiotach przewodzących. Są to wielkości bezpośrednio odczytywane na miernikach.

• Równanie
  (makroskopowe) jest odpowiednikiem równania
  (mikroskopowe). Równania te są ogólnymi definicjami oporu materiału R i jego oporności właściwej
  niezależnie czy dany materiał spełnia prawo Ohma czy nie

• Jeżeli opór materiału R nie zależy od V oraz od i (opór właściwy
  nie zależy od E oraz od j), to oznacza, że dany przewodzący materiał spełnia prawo Ohma

24. Energia i moc prądu elektrycznego

• Załóżmy, że na końcówkach rezystora, przez który płynie prąd I, występuje różnica potencjałów (napięcia) U.

• Podczas przepływu prądu I przez przekrój poprzeczny przewodnika w czasie t przemieści się ładunek, Q = I × t .

• Energia zużytkowana na przemieszczenie tego ładunku W = U × Q = U × I × t. Energia ta wydziela się na rezystorze w postaci ciepła. Jednostką energii jest 1 dżul (1 J) [W] = [U] [I] [t] = V×A×s = W×s = J. Jednostka energii elektrycznej - dżul - jest więc iloczynem dwóch jednostek : wata i sekundy.

• 2. Energię można wyrazić za pomocą innych wielkości elektrycznych: Korzystając z prawa Ohma w postaci U = I×R, otrzymamy wzór na energię W = R × I² × t, a w postaci I = G × U, otrzymamy W=U² × t/R

• 3. Równanie W = R×I²×t, wyraża prawo Joule'a-Lenza zgodnie z którym energia elektryczna przekształcana na rezystancji w ciepło, jest wprost proporcjonalna do kwadratu prądu I, rezystancji przewodnika R i czasu t.

• 4. Stosunek energii prądu elektrycznego do czasu nazywamy mocą elektryczną i oznaczamy przez P, zatem
  . Jednostką mocy jest 1 wat (1W = 1J/1s). Wat jest to moc, przy której praca wykonana w czasie jednej sekundy jest równa jednemu dżulowi. Moc elektryczna jest równa iloczynowi napięcia i prądu. Jeżeli do wzoru na P podstawimy zależności na W, to otrzymamy P = R×I²

25. Obwody elektryczne. Prawa Kirchoffa

• Pierwsze prawo Kirchhoffa:

• Twierdzenie o punkcie rozgałęzienia. Algebraiczna suma natężeń prądów przepływających przez punkt rozgałęzienia (węzeł) jest równa zeru.

• 
  

• Drugie prawo Kirchhoffa:

• Twierdzenie o obwodzie zamkniętym. Algebraiczna suma sił elektromotorycznych i przyrostów napięć w dowolnym obwodzie zamkniętym jest równa zeru (spadek napięcia jest przyrostem ujemnym napięcia).

• 
  

• Twierdzenie o obwodzie zamkniętym jest wynikiem zasady zachowania energii, a twierdzenie o punkcie rozgałęzienia wynika z zasady zachowania ładunku. Przy stosowaniu praw Kirchhoffa zakładamy jakiś kierunek prądu i jego natężenie w każdej gałęzi. Spadek napięcia pojawia się gdy "przechodzimy" przez opornik w kierunku zgodnym z przyjętym kierunkiem prądu, a przyrost napięcia gdy przechodzimy przez źródło SEM w kierunku od "−" do "+". Jeżeli w wyniku obliczeń otrzymamy ujemne natężenie prądu to znaczy, że rzeczywisty kierunek prądu jest przeciwny do przyjętego.

26. Linie indukcji i strumień pola magnetycznego. Prawo Gaussa dla pola magnetycznego.

• Liniami indukcji pola:

• Styczna do linii indukcji w dowolnym pkt. Wyznacza kierunek wektora indukcji pola mag. W tym pkt.

• Linie indukcji wykreśla się tak, że liczba linii fi ( strumień pola) na jednostce powierzchni danego przekroju
  jest wartość indukcji magnetycznego B w tym przekroju. Gdy linie leżą blisko siebie ( duża gęstość linii), indukcja jest duża, gdy są odległe ( mała gęstość linii) indukcja jest mała (rys.)

• Strumień pola
  ( skalar!!!) jest miarą ilości linii sił pola przenikającego dany przekrój dS

• 
  różniczkowo
  

• Element powierzchni dS jest wektorem o wartości równej polu tej powierzchni oraz kierunku i zwrocie Normalnej Zewnętrznej (wektor prostopadły do powierzchni i skierowany na zewnątrz niej) (rys.)

• Strumień powierzchni przenikający dany element powierzchni może być dodatni, zerowy lub ujemny (rys.)

• Aby obliczyć strumień przenikający całą powierzchnię należy obliczyć całke powierzchniową:
  dla powierzchni otwartej,
  dla powierzchni zamkniętej

• Prawo Gaussa

• Całkowity strumień pola magnetycznego przenikający zamkniętą powierzchnię jest równy zero!!
  

• Należy pamiętać, że powierzchnia Gaussa jest powierzchnią zamkniętą!!

• Z prawa Gaussa dla pola magnetycznego wynika, że nie ma pojedynczych biegunów- monopoli magnetycznych. Zawsze występują (dwubiegunowe) dipole (N-S)

• Linie pola magnetycznego nigdzie się nie zaczynają i nigdzie nie kończą

27. Parametry pola magnetycznego ( strumień, natężenie, indukcja), zależności i jednostki!

• Strumień magnetyczny
  

• Indukcja magnetyczna
  

• 
  

• Natężenie pola magnetycznego
  

• Względna przenikalność magnetyczna ośrodka
  

• Przenikalność magnetyczna próżni
  

28. Przenikalności i własności magnetyczne materiałów

• Wartości przenikalności
  decydują o właściwościach magnetycznych materiałów

• 
  diamagnetyki ( wypchane z pola magnetycznego)

• 
  próżnia

• 
  paramagnetyki ( wciągnięte w pole magnetyczne)

• 
  ferromagnetyki (silnie wciągane w pole magnetyczne)

• Dal wybranych materiałów

• Miedz
  (diamagnetyk)

• Powietrze
  (paramagnetyk)

• Anizotropowa blacha elektrotechniczna
  (ferromagnetyk)

29. Siła Lorentza, ruch cyklotronowy,

• Siła Lorentza — siła, jaka działa na cząstkę obdarzoną ładunkiem elektrycznym poruszającą się w polu elektromagnetycznym. Wzór podany został po raz pierwszy przez Lorentza i dlatego nazwano go jego imieniem.

Wzór określa, jak siła działająca na ładunek zależy od pola elektrycznego i pola magnetycznego (składników pola elektromagnetycznego):

gdzie:

• F - siła (w niutonach),

• E - natężenie pola elektrycznego (w woltach / metr),

• B - indukcja magnetyczna (w teslach),

• q - ładunek elektryczny cząstki (w kulombach),

• v - prędkość cząstki (w metrach na sekundę),

Terminem siła Lorentza określa się czasem samą składowa magnetyczną tej siły

• Ruch cyklotronowy. W stałym polu magnetycznym B ładunek Q porusza sie po okręgu o promieniu R lub po spirali

30. Siła elektrodynamiczna

• Siła elektrodynamiczna (magnetyczna) - siła, z jaką działa pole magnetyczne na przewód elektryczny, w którym płynie prąd elektryczny. Na umieszczony w polu magnetycznym o indukcji magnetycznej B prostoliniowy przewodnik o długości l, przez który płynie prąd o natężeniu I, działa siła F, którą wektorowo określa wzór:

czyli jej wartość wynosi:

Kąt α jest to kąt między kierunkiem przepływu prądu a kierunkiem linii pola. Kierunek siły jest prostopadły do linii pola magnetycznego i przewodu. Zwrot siły określa reguła lewej dłoni.

Zjawisko oddziaływania pola magnetycznego na przewodnik skutkuje też wytwarzaniem prądu w trakcie jego przemieszczania w polu magnetycznym. Napięcie elektryczne wytwarzane w ten sposób jest nazywane siłą elektromotoryczną indukcji.

• Siła elektrodynamiczna jest to siła oddziaływania pola magnetycznego nad przewodnik z prądem. Siła elektrodynamiczna jest prostopadła do wektora natężenia pola magnetycznego oraz jest prostopadła do przewodnika z prądem.

oraz

- traktujemy jako wektor którego:

a) wartość jest równa długości przewodnika

b) kierunek jest zgodny z przewodnikiem

c) Zwrot jest zgodny z kierunkiem prądu.

Zwrot siły elektrodynamicznej zależy od kierunku prądu oraz od zwrotu natężenia pola magnetycznego. Jeżeli prąd zmienia kierunek lub natężenie pola magnetycznego zmienia zwrot, to siła elektrodynamiczna też zmienia zwrot.

Wartość siły elektrodynamicznej jest wprost proporcjonalna do natężenia prądu, natężenie pola magnetycznego oraz do długości przewodnika

F ~ I , F ~ H , F ~ L

Z powyższych wniosków wynika, że siła elektrodynamiczna dana jest wzorem:

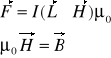
- wektor indukcji magnetycznej

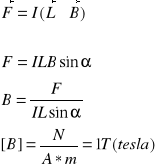
31. Pole magnetyczne przewodnika, w którym płynie prąd ( prawo Apmrere'a, prawo Biota-Savarta)

• Prawo Ampere'a (rys.)

• Całka (krzywo)liniowa z indukcji magnetycznej jest równa sumie wszystkich prądów przepływających przez powierzchnię otoczoną ( zamkniętą krzywą całkowania)

• 
  

• Prawo Biota-Savarta

• Przyczynek
  do pola indukcji magnetycznej w danym punkcie A od elementu długości
  przewodnika z prądem o natężeniu I.

zwana stałą magnetyczną

- natężenie prądu, wyrażone w amperach,
- skierowany element przewodnika; wektor o kierunku przewodnika, zwrocie odpowiadającym kierunkowi prądu i długości równej długość elementu przewodnika,
- wersor dla punktów wytwarzającego pole (elementu przewodnika) i miejsca pola,
- odległość elementu przewodnika od punktu pola.

Inna postać wzoru:

Gdzie
to wektor wodzący o początku w źródle pola i końcu w rozważanym punkcie przestrzeni. Wartość indukcji magnetycznej może być obliczona ze wzoru

Rozciągły obszar z prądem

Wyżej przytoczony wzór jest prawdziwy dla cienkich przewodników z prądem dla obszarów, w których płynie prąd w dużych objętościach wzór przyjmuje postać:

- gęstość prądu, dV - element objętości

Poruszający się ładunek

q - ładunek elektryczny,
- prędkość ładunku.

Pole w danym punkcie

Całkowitą indukcję magnetyczną wyznacza się całkując różniczkowe elementy indukcji
wzdłuż całego przewodnika - w pierwszym wzorze, a w całym obszarze, w którym płynie prąd w drugim wzorze.

Wnioski

Wzór Biota - Savarta umożliwia obliczenie indukcji magnetycznej, gdy znane jest natężenie prądu, który jest źródłem pola magnetycznego (punkty tego pola są scharakteryzowane przez wektor indukcji, a wartość tego wektora określa wzór Biota - Savarta).

Wszystkie przyczynki do wektora indukcji pochodzące od elementów przewodnika mają w danym punkcie taki sam kierunek, który jest prostopadły do płaszczyzny, w której leży przewodnik i analizowany punkt. Dlatego pole magnetyczne ma kształt okręgów leżących w płaszczyźnie prostopadłej do przewodnika, środkami, których jest przewodnik, a indukcję magnetyczną w próżni określa wzór:

I - natężenie prądu, r - odległość od przewodnika.

Wzór ten jest słuszny w małej odległości od przewodnika lub w dowolnej odległości dla nieskończenie długiego przewodnika. W przypadku przewodnika nieliniowego indukcję pola magnetycznego w dowolnym punkcie przestrzeni można otrzymać całkując wzór Biota - Savarta po całej długości przewodnika. Na przykład w środku przewodnika kołowego o promieniu R w próżni prowadzi to do wyrażenia

32. Prawo indukcji Faradaya, reguła Lentza

• Prawo indukcji Faradaya

• Zmienny strumień magnetyczny
  przenikający pole powierzchni S indukuje pole elektryczne E „przecałkowane” po długości wprowadzonego przewodnika ( obejmującego powierzchnię S (a->b)) powoduje powstanie na jego końcach różnicy potencjałów (rys.)

• Po zwarciu przewodnika po wpływem SEM popłynie prąd i, który wytworzy właśnie pole magnetyczne
  

• „minus” w prawie indukcji Faradaya jest odzwierciedleniem reguły Lentza (prądy i powstałe w wyniku indukcji (i ich pola magnetyczne
  ), będą przeciwdziałały przyczynie, która je wywołała (
  )). Decyduje to o kierunkach indukowanych napięć, prądów i strumieni.

• Prawo indukcji umożliwia budowanie generatorów i silników

• Są różne techniczne sposoby zmiany strumienia „widzianego” przez pętlę przewodnika ( np. wirujące ramki przewodnika w polu magnetycznym - SEM sinusoidalnie zmienne)

• Na zasadzie indukcji prądów wywołanych przez wirujące pole magnetyczne działają silniki asynchroniczne

• Pole elektryczne powstające w wyniku indukcji nie jest polem zachowawczym.

33. Metody indukowania pola magnetycznego

• Zmienny strumień elektryczny (
  ) przenikający pole powierzchni S indukuje pole magnetyczne „przecałkowane” po obwodzie powierzchni S daje

• Dwie metody indukowania pola magnetycznego

• Zjawisko symetryczne do zjawiska Faradaya (rys.)

• 
  

• Prawo Ampere'a (rys.)

• 
  

• Ogólnie

• 
  

• Uwagi:

• Omówione zjawiska pokazują, że indukowane pole elektryczne (magnetyczne) powstaje w płaszczyźnie (lokalnie) prostopadłej do wywołującego je strumienia magnetycznego ( elektrycznego)

• Ma to szczególnie znaczenie w powstawaniu i propagacji fal elektromagnetycznych (rys.)

34. Solenoid, napięcie samoindukcji, transformator

• (rys.)

• W miarę jak solenoid staje się coraz bardziej idealny, tzn. w miarę jak zbliża się do nieskończenie długiego cylindra, w którym płynie prąd i, pole magnetyczne w pkt. zewnętrznych dąży do zera

• Wewnątrz idealnego solenoidu indukcja B nie zależy od jego wymiarów (średnicy i długości) i jest stała na całej powierzchni przekroju poprzecznego

• Otrzymane równanie na B można również w sytuacji, gdy solenoid składa się z wielu warstw zwojów (zmianie ulega n)

• Otrzymane równanie można stosować również w przypadku solenoidów rzeczywistych dla pkt. leżących blisko środka cewki.

m₁

m₂

r₁₂

F₁₂

---