3 Właściwości optyczne i elektryczne materii. Pomiar współ­czynnika załamania w funkcji stężenia i temperatury.

Światło ma naturę złożoną, ponieważ wykazuje własności falowe i korpuskularno kwantowe. W fali elektromagnetycznej drganiom podlegają wektory E i H. Procesy fizjologiczne, fotochemiczne, fotoelektryczne i wiele innych, które za­chodzą pod wpływem światła, są wynikiem działania wektora elektrycznego. Oznaczając wartość bezwzględną amplitudy wektora elektrycznego fali świetl­nej przez E_­­­­­­­­_m można jej zmianę w czasie wzdłuż kierunku jej rozchodzenia się wyrazić wzorem:

gdzie:

k - liczba falowa,

r - odległość od źródła fali w kierunku jej rozchodzenia. Należy pamiętać, że amplituda fali kulistej w ośrodku maleje jak 1/r. Światło w ośrodku jednorodnym i izotropowym wykazuje charakterystycz­ne właściwości:

- rozchodzi się po liniach prostych (zasada Fermata),

- promienie są niezależne od siebie — nie zakłócają się wzajemnie,

- ulegają odbiciu od powierzchni o innej gęstości optycznej,

- załamują się na granicy ośrodków o różnej gęstości optycznej. Stosunek prędkości rozchodzenia się fali świetlnej w próżni c do prędkości fazowej y w danym ośrodku określa bezwzględny współczynnik załamania n danego ośrodka:

Względny współczynnik załamania definiuje się jako stosunek prędkości fazo­wej ν₁ w ośrodku pierwszym do prędkości fazowej υ₂ w ośrodku drugim:

Wartość współczynnika załamania charakteryzuje gęstość optyczną ośrodka.

Ośrodek o większym względnym współczynniku załamania nazywa się oś­rodkiem optycznie gęstszym, o mniejszym zaś — optycznie rzadszym. Wyzna­czając z równania prędkość υ, można względny współczynnik załamania ośrodka drugiego względem pierwszego wyrazić wzorem:

Z wyrażenia wynika, że względny współczynnik załamania dwóch ośrod­ków jest równy stosunkowi ich bezwzględnych współczynników załamania. Współzależność prędkości, częstotliwości oraz długości fali jest następująca:

Ponieważ częstotliwość v jest wielkością stałą dla danej fali) to zmiana prędko­ści fazowej pociąga za sobą zmianę długości fali λ. W dowolnym ośrodku prędkość fazowa fali jest mniejsza niż w próżni. Wynika stąd, że długość fali λ w danym ośrodku jest mniejsza niż w próżni λ₀ Zależność, jaka zachodzi w tym przypadku, jest następująca:

Z równań Maxwella wynikają następujące równania falowe:

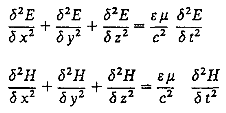
Prędkość fazowa fal elektromagnetycznych jest określona wyrażeniem:

gdzie:

ε - względna przenikalność elektryczna,

μ - względna przenikalność magnetyczna.

Przyjmuje się, że dla próżni: ε =μ=1. Jak wynika ze wzoru pręd­kość fali elektromagnetycznej jest taka sama jak prędkość światła. Porównując równanie z wyrażeniem otrzymuje się współzależność parametru optycznego z parametrami elektromagnetycznymi materii w postaci:

Dla przeważającej większości ciał przezroczystych, dla światła współczynnik określający właściwości magnetyczne ciała jest bliski jedności i można go pomi­nąć. Przy tym założeniu otrzymuje się, że:

W literaturze wyrażenie (14.10) nosi nazwę wzoru Maxwella. Związek ten jest słuszny dla ośrodków niemagnetycznych i tylko wtedy, gdy zarówno n, jak i ε są wyznaczane dla pól o tej samej częstości ω. Podawana w tablicach wartość przenikalności elektrycznej ε dla wody wynosi 81. Wynikałoby z tego, że n = 9, gdy tymczasem n wynosi 1.333. Ta pozorna sprzeczność wynika stąd, że podana w tablicach wartość ε wyznaczona została dla pól elektrostatycz­nych. W szybkozmiennych polach, dla których częstości ω są porównywalne z częstościami promieniowania, otrzymuje się wartości współczynnika załama­nia zgodne z równaniem Maxwella. Okazało się, że przenikalność elektryczna ośrodka zależy od częstości działającego pola - rysunek 14.1.

Na fakcie tym opiera się wyjaśnienie zjawiska dyspersji światła, tzn. zależności: n = f(ω). Funkcja ta ma swoje uzasadnienie w tym, że współczynnik załamania zależy od właściwości atomów ośrodka i częstości padającego światła, co wyni­ka ze wzoru:

gdzie:

N — liczba elektronów w jednostce objętości, ω₀ — częstość drgań własnych elektronów w atomie,

ω — częstość padającego światła.

Jeżeli wprowadzić dowolną substancję w jednorodne pole elektryczne, to cząsteczki tego ciała będą doznawać dwóch efektów. Pierwszy polega na tym, że, chmura ujemnych elektronów, która otacza pojedyncze atomy w każdej cząsteczce, zostaje zniekształcona i przesunięta pod wpływem pola. W wyniku tego zniekształcenia środki dodatnich i ujemnych ładunków układu przestają się pokrywać w przestrzeni, na skutek czego cząsteczka — dotychczas elekt­rycznie izotropowa — uzyskuje pod wpływem pola moment dipolowy elekt­ryczny, który decyduje o jej zachowaniu się względem innych cząsteczek. Oba ładunki są równe i przeciwnych znaków, zatem cząsteczka jako całość pozos­taje obojętna. Ponieważ oba bieguny występują tylko w obecności zewnętrz­nego pola, zjawisko to jest nazywane polaryzacją elektronową; o cząsteczkach mówi się, że mają indukowany moment dipolowy. Im silniejsze jest pole i bar­dziej ruchliwa chmura ładunków, tym większa jest polaryzacja cząsteczki w po­lu o jednostkowym natężeniu.

Drugi efekt dotyczy cząsteczek, w których środki ciężkości ładunków do­datnich i ujemnych nie pokrywają się z przyczyn związanych z ich budową wewnętrzną. Cząsteczki te niezależnie od istnienia pola zewnętrznego mają własny moment dipolowy elektryczny i nazywa się je polarnymi.

W jednorodnym polu elektrycznym niepolarne cząsteczki orientują się osią swej więksuej zdolności polaryzacyjnej równolegle do pola (efekt indukcyj­ny), natomiast cząsteczki polarne orientują się osią swych trwałych momentów w kierunku pola (efekt kierunkowy). Ważne jest odróżnienie tych dwóch efek­tów, gdy występują one w tej samej cząsteczce. DEBYE wykazał, że efekt kierun­kowy zależy od temperatury, ponieważ ruchy termiczne wtórne zakłócają orientację dipoli.

Wielkością, która określa stopień uporządkowania dipoli w dielektryku, jest moment dipolowy jednostki objętości: i

Wektor P nazywa się wektorem polaryzacji lub spolaryzowaniem dielektryka i ma wymiar Cm^-2. W dowolnym dielektryku wektor polaryzacji jest wprost proporcjonalny do natężenia pola elektrycznego, które na niego działa:

gdzie:

χ — wielkość bezwymiarowa, niezależna od natężenia pola, nosi na­zwę podatności elektrycznej materiału.

W przypadku jednego atomu, który znajduje się w zmiennym polu o natężeniu E, środek ładunku elektronów musi spełniać równanie:

gdzie:

q₀ — ładunek elektronu,

m — masa elektronu.

Pierwszy wyraz tego równania jest iloczynem masy i przyspieszenia, drugi przedstawia siłę dążącą do przywrócenia równowagi, a po prawej stronie wy­stępuje siła od zewnętrznego pola. Jeżeli pole zewnętrzne zmienia się z częstoś­cią ω, to rozwiązaniem równania (14.14) jest wyrażenie:

W tym przypadku podatność atomu na działanie pola określa się jako a i nazy­wa polaryzowalnością atomową, ma ona wymiar m³. Wartość jej określa wyra­żenie:

Rozpatrywaliśmy dotychczas zdolność • polaryzacyjną cząsteczek jako wielkość skalarną, w istocie zaś zdolność polaryzacyjna nieizotropowych cząs­teczek jest różna w różnych kierunkach. Cząsteczki o symetrii osiowej mają dwie zdolności polaryzacyjne, natomiast asymetryczne cząsteczki - trzy. Pod­czas pomiarów polaryzacji za pomocą współczynnika załamania światła anizo­tropia ta nie jest dostrzegalna, ponieważ cząsteczki badanej substancji są roz­mieszczone bezładnie i efekt wypadkowy jest równy zero. Anizotropia zdolno­ści polaryzacyjnej daje się zaobserwować jedynie wtedy, gdy poszczególne cząsteczki są skierowane w sposób określony. Przypadek ten zachód/i w krysz­tałach nieregularnych oraz w gazach i cieczach poddanych działaniu pola elek­trycznego (efekt Kerra). Jeżeli w jednostce objętości znajduje się N atomów, to wektor polaryzacji będzie równy:

Korzystając z zależności, że:

można wzór (14.17) napisać w postaci:

Iloczyn N σ określa polaryzowalność na jednostkę objętości. Zależy ona od temperatury w jakiej się ciało znajduje i częstości pola działającego na dielekt­ryk. Korzystając ze wzoru (14.16), można wyrażenie (14.19) zapisać:

Związek, jaki zachodzi pomiędzy polaryzowalnością i podatnością elektryczną, jest następujący:

W praktyce wyznacza się polaryzowalność molową, tzn. odniesioną do liczby cząsteczek w jednym molu N₀, (liczba Avogadra).

gdzie:

M - ciężar cząsteczkowy,

p - gęstość bezwzględna.

Wyrażenie nosi w literaturze nazwę równania CLAUSIUSA-MOSSOTTIEGO. Podstawiając równanie do wyrażenia, otrzymuje się rów­nanie Lorentza-Lorenza, Na tzw. refrakcję molową R w postaci:

Z punktu widzenia optycznego, np. wzrost refrakcji molowej oznacza zawsze rozluźnienie chmury ładunków ujemnych w atomach tworzących cząsteczkę. Z wyrażenia wynika, że przenikalność elektryczna różnych gazów zale­ży od ich gęstości i częstości ω₀, jego absorpcji optycznej.

W kryształach jonowych poszczególne cząsteczki zatracają swoje indywi­dualne cechy. Cały kryształ zachowuje się tak jak jedna duża cząsteczka. Sieć

kryształu jonowego można traktować jako dwie przenikające się sieci, jedną zbudowaną z jonów dodatnich, drugą - z jonów ujemnych. Pod wpływem zewnętrznego pola elektrycznego obie sieci przesuwają się względem siebie, co prowadzi do polaryzacji dielektryka. Pomiędzy wektorem indukcji elektrycznej D a wektorami natężenia pola elektrycznego i polaryzowalnością zachodzi na­stępujący związek:

Podstawiając wzór do wyrażenia, otrzymuje się:

Wyrażenie w nawiasie, tzn. (l + χ) = ε, jest bezwymiarowe i nazywa się względną przenikalnością elektryczną lub przenikalnością elektryczną ośrodka. Wyko­rzystując powyższe oznaczenie, można wyrażenie zapisać:

Zależność (14.26) jest spełniona tylko dla dielektryków izotropowych. W przy­padku dielektryków anizotropowych wektory E i D nie są w ogólności współliniowe.

Rozpatrzmy jak zachowuje się płaska fala elektromagnetyczna, opisana równaniem (14.1), padająca na granicę dwóch ośrodków o różnych współczyn­nikach załamania. Niech wektor k określający kierunek rozchodzenia się fali padającej w pierwszym ośrodku leży w płaszczyźnie rysunku (rys. 14.2).

Kierunek normalnej do powierzchni rozdziału niech określa wektora n Płaszczyzna, w której leżą wektory k i n, nazywa się płaszczyzną padania fali. Kierunek rozchodzenia fali odbitej określa wektor k₁ załamanej zaś k₂.

W ośrodku jednorodnym i izotropowym oba te wektory leżą w płaszczyź­nie padania fali. Zgodnie z prawem odbicia, promień odbity leży w tej samej płaszczyźnie co promień padający i prosta prostopadła w miejscu padania promienia, kąt odbicia równa się kątowi padania, a prędkości ich są równe. Natomiast z prawa załamania (14.3) wynika, że promień załamany leży w tej samej płaszczyźnie co promień padający i prosta prostopadła. Korzystając ze wzoru, można prawo załamania napisać w postaci:

gdzie:

α - kąt padania promienia w ośrodku pierwszym,

β - kąt załamania w ośrodku drugim.

Ze wzoru tego wynika, że przy przechodzeniu światła z ośrodka optycznie gęstszego do optycznie rzadszego promień załamany odchyla się od normalnej do powierzchni rozdziału ośrodków. Zwiększeniu kąta padania a odpowiada wzrost kąta załamania β. Jeżeli kąt α osiągnie wartość.

to kąt β staje się równy ∏/2. Kąt padania, przy którym kąt załamania wynosi 90°, nazywa się kątem granicznym α_gr

Energia niesiona przez promień padający rozdziela się na promień odbity i załamany. W miarę wzrostu kąta padania a, natężenie promienia odbitego rośnie, a załamanego maleje, przyjmując wartość równą zero dla kąta granicz­nego. Gdy kąt padania zawiera się w przedziale od kąta granicznego α_gr do Π/2, fala świetlna wnika do ośrodka drugiego na głębokość rzędu długości fali, a następnie powraca do ośrodka pierwszego. Zjawisko to nazywa się całkowi­tym odbiciem wewnętrznym jest wykorzystane m.in. w refraktometrze Abbego. Zasada działania refraktometru Abbego jest podana na rysunku

Zasadniczą częścią refraktometru są dwa prostokątne pryzmaty ABC i DFE złożone razem przeciwprostokątnymi AC i DE (rys. 14.3a). Pryzmaty te są wykonane ze szkła o dużym współczynniku załamania, który powinien być większy od współczynnika załamania cieczy mierzonej. Jeżeli wprowadzimy między ścianki pryzmatów dwie, trzy kropelki cieczy mierzonej, to utworzy ona warstwę płaskorównoległą Gdy na ściankę EF pada pod kątem zero równoległa monochromatyczna wiązka światła, wówczas na warstwie cie­czy ulegnie tylko równoległemu przesunięciu o wartość:

gdzie:

n₁ — współczynnik załamania pryzmatów,

n₂ - współczynnik załamania cieczy,

d - grubość warstwy cieczy,

α - kąt padania promienia na warstwę cieczy.

Tak będzie, gdy kąt padania a jest mniejszy od kąta granicznego. Jeżeli będzie­my obracać układ pryzmatów dokoła osi przechodzącej przez środek pola ACED, prostopadłej do płaszczyzny rysunku, to przy zwiększaniu kąta pada­nia na płaszczyznę ED doprowadzimy do tego, że będzie on równy kątowi granicznemu. Dla wszystkich promieni, które będą padać pod ką­tem większym od kąta granicznego, nastąpi całkowite wewnętrzne odbicie od powierzchni ED. W tym przypadku pole widzenia w okularze lunetki będzie ciemne. Gdy układ pryzmatów będzie ustawiony tak, że kąt padania promieni będzie bliski kątowi granicznemu, wówczas w polu widzenia zauważymy ostro zaznaczone przejście między polem oświetlonym a ciemnym. Granica ta od­powiada kątowi granicznemu. Dokładnego ustawienia na kąt graniczny doko­nuje się pokrętłem, które w polu widzenia okularu przesuwa granicę między polem jasnym i ciemnym tak długo, aż pokryje się ona z przecięciem krzyża widocznym w okularze. Po takim nastawieniu na dolnej skali widocznej w oku­larze odczytuje się wartość współczynnik załamania oraz procentową zawar­tość rozpuszczonej substancji w roztworze. Dokładność odczytu współczyn­nika załamania w tego typu refraktometrach jest rzędu 0.0005. Do każdego refraktometru jest dołączona tabelka przeliczeniowa na wartości współczyn­nika załamania dla kilku długości fal świetlnych używanych do oświetlenia refraktometru. Przy użyciu światła białego zamiast granicy cienia i jasności

otrzymuje się, w wyniku zależności współczynnika załamania od długości fali, rozmyty pasek barwny.

Refraktometry mają układ termostatujący pryzmaty, gdyż współczynnik załamania zależy od temperatury i przy tak dużej dokładności odczytu różnice są mierzalne.

---