Temat: Wyznaczanie współczynnika załamania światła metodą najmniejszego odchylenia w pryzmacie

1. Wstęp.

Załamanie światła na powierzchni rozgraniczającej dwa ośrodki opisane jest prawem Snella

(1.1)

gdzie α - kąt padania światła na granicę ośrodków, β - kat załamania, n - współczynnik załamania ośrodka drugiego względem pierwszego.

Gdy pierwszy z ośrodków jest próżnią, równanie (1) definiuje bezwzględny współczynnik załamania, w innych przypadkach współczynnik względny.

Prawa Snella w postaci (1) nie używa się do praktycznego wyznaczania ze względu na niedogodność i niedokładności wyznaczania kątów padania i załamania, natomiast możemy je skutecznie zastosować do pryzmatu gdzie kąty α i β można wyrazić przez inne, dogodne do pomiaru wielkości.

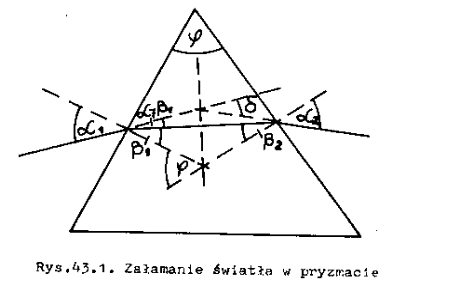
Rys. 1.1. Załamanie światła w pryzmacie

W ćwiczeniu wykorzystujemy tylko dwie płaszczyzny pryzmatu, tworzące między sobą kąt ϕ, zwany kątem łamiącym. Promień świetlny padający na pryzmat ulega dwukrotnemu załamaniu i zostaje odchylony o pewien kąt δ (rys.1.), zależny od kąta padania α oraz od kąta łamiącego ϕ . Na podstawie rysunku kąt odchylenia wyraża się następująco:

(1.2)

Kąt padania można tak dobrać, aby promień biegnący wewnątrz pryzmatu był prostopadły do dwusiecznej kąta łamiącego ϕ . W tej sytuacji bieg promienia jest symetryczny, tzn. α₁=α₂ oraz β₁=β₂, a kąt odchylenia jest najmniejszy z możliwych dla danego pryzmatu

Biorąc ponadto pod uwagę, że 2β = ϕ , możemy przekształcić równanie (2) do postaci

(1.3)

Podstawiając wyrażone powyżej wartości α i β do wzoru (1), definiującego współczynnik załamania, otrzymamy

(1.4)

Stosując powyższy wzór możemy wyznaczyć współczynnik załamania n na podstawie pomiarów kąta łamiącego i kąta najmniejszego odchylenia.

W przypadku gdy dwusieczna kąta łamiącego jest w przybliżeniu równoległa do światła padającego na pryzmat to jedna część wiązki ulega odbiciu na lewo, a druga na prawo od kierunku pierwotnego biegu. Z tego wynika, że
, skąd

 (

2. Przebieg ćwiczenia.

1. Pomiar kąta prawego _p oraz dwusiecznej kąta łamiącego  dla różnych długości fali .

W związku z awarią spektrometru nie przeprowadzono pomiarów dla _l. Wobec powyższego zmierzony został kąt  oraz kąt _p i z tych wyników pomiarów zostaną przeprowadzone obliczenia.

Ze wzoru 1.5 obliczamy  (np. dla pomiaru pierwszego)

Z przekształcenia wzoru 1.3 wynika następująca zależność:

,

stąd podstawiając do wzoru 1.4 otrzymujemy:

.

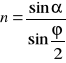
Przykładowe obliczenie dla pomiaru pierwszego:

.

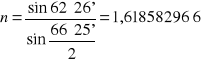
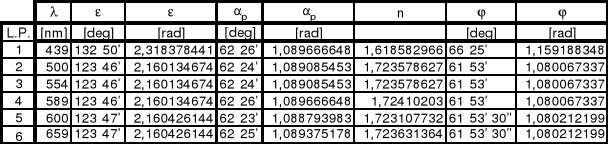
Wyniki pomiarów i obliczeń zawiera tabela 2.1.

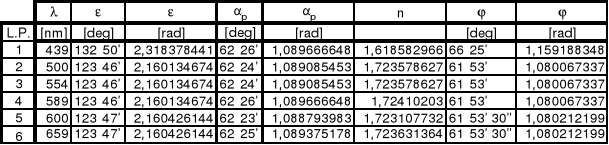
Tabela 2.1.

2. Obliczenie błędów pomiarowych.

Błąd odczytu z podziałki spektrometru wynosi ±1' co w przeliczeniu na radiany wynosi:

.

Błąd pomiaru  wynosi (dla pomiaru pierwszego):

stąd dla pomiaru pierwszego:

Błąd pomiaru współczynnika załamania światła n dla pomiaru pierwszego:

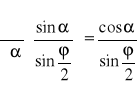
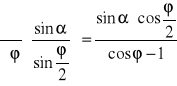
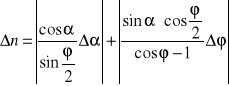
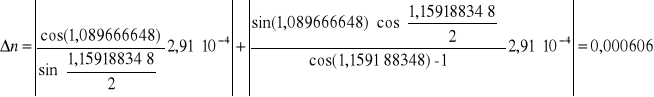
Pozostałe wyniki zawarto w tabeli 2.2.

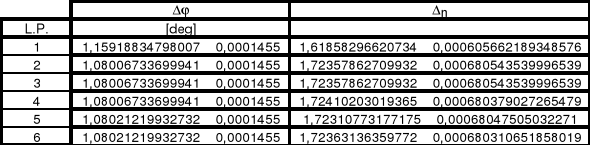
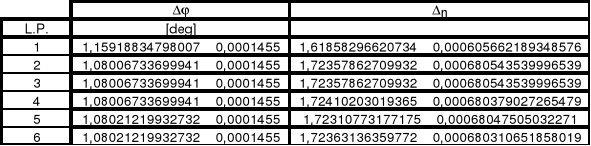
Tabela 2.2.

3. Wnioski.

Wartość kąta najmniejszego odchylenia maleje wraz ze wzrostem długości fali. Jak wynika z wykresu wartość współczynnika załamania światła maleje wraz ze wzrostem długości światła padającego na pryzmat. Światło o barwie czerwonej (filtry nr 4) zostało załamane o najmniejszy kąt, światło fioletowe (filtr nr 9) o największy.

---