Sprawdzenie stanu granicznego nośności elementów konstrukcji stalowych
siła wewnętrzna od obciążeń obliczonych
- nośność obliczeniowa przekroju elementu konstrukcyjnego bądź nośność łączników.
zredukowana wartość wytrzymałości obliczeniowej
zredukowany współczynnik prężności podłużnej E
zredukowany współczynnik niestateczności ϕ
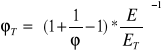
ELEMENTY ROZCIĄGANE
przy rozciąganiu osiowym 
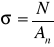
przy rozciąganiu mimośrodowym:
- przypadek zginania w jednej płaszczyźnie 
- przypadek zginania w dwóch płaszczyznach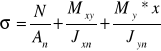 
gdzie:
-
to pole przekroju netto, wskaźnik wytrzymałości netto dla włókien rozciąganych, momenty bezwładności netto względem osi
-X, Y: X, Y - to odległości krawędzi przekroju odpowiednio od osi X i Y. N - obliczeniowa wartość siły rozciągającej.
-M, Mx, My - to obliczeniowa wartość momentów zginających.
Elementy rozciągane osłabione otworami na łączniku wymagają określenia sprowadzonego pola przekroju 
według wzoru:
- dla ścianki elementu lub blachy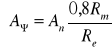 
; 
-dla elementów złożonych warunek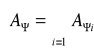 
Gdzie:
najmniejsze (minimalne) pole przekroju płaskiego lub łamanego netto
- pole przekroju brutto.
granica wytrzymałości i plastyczności materiału.
Nośność elementów rozciąganych sprawdza się według wzorów:
a) przy rozciąganiu osiowym 
lub 
,
gdzie:
obliczeniowa wartość siły rozciągającej
obliczeniowa nośność przekroju elementu rozciąganego
gdzie: A - pole przekroju poprzecznego pręta
pole przekroju sprawdzone
wytrzymałość obliczeniowa stali
b) przy rozciąganiu mimośrodowym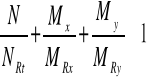 
oraz 
gdzie:
N - obliczeniowa wartość siły rozciąganej
- to obliczeniowa wartość momentu zginającego w płaszczyźnie prostopadłej odpowiednio do osi xx i yy.
- obliczeniowa nośność przy zginaniu w płaszczyźnie prostopadłej odpowiednio do osi x-x i y-y.
ELEMENTY ŚCISKANE
przypadku najprostszym (ściskania osiowego) bezpieczeństwo elementu ściskanego opisuje nierówność 
Czyste ściskanie (bez uwzględnienia wyboczenia) według wzoru: 
,
gdzie:
- obliczeniowa wartość siły ściskającej ,
- pole przekroju pręta netto
Długość wyboczeniowa pręta ściskanego Oblicza się ze wzoru 
,
gdzie:
współczynnik długości wyboczeniowej;
teoretyczna długość pręta..
Smukłość wyznacza się ze wzoru 
gdzie: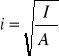 
i - promień bezwładności przekroju pręta
I - moment bezwładności pręta:
A- pole przekroju pręta .
Smukłość porównawczą wyznacza się ze wzoru :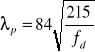 
,
w którym 
wytrzymałość obliczeniowa stali w (MPa).
NOŚNOŚĆ ELEMENTÓW POJEDYŃCZYCH ŚCISKANYCH OISOWO
nośność obliczeniową przekroju przy osiowym ściskaniu : 
,
Gdzie:
A - pole przekroju poprzecznego pręta
wytrzymałość obliczeniowa stali
współczynnik wpływu niestateczności miejscowej na niestateczność ogólną.
Nośność prętów pojedynczych ściskanych osiowo z uwzględnieniem wyboczenia giętnego sprawdza się według wzorów: 
gdzie:
N- obliczeniowa wartość siły ściskającej
ϕ - współczynnik niestateczności ogólnej
obliczeniowa nośność przekroju na ściskanie.
ELEMENTY ZGINANE
NOŚNOŚĆ ELEMENTÓW ZGINANYCH JEDNOKIERUNKOWO
nośność obliczeniową przekroju 
według wzorów:
1) dla przekrojów klas 1, 2, 3 
=
:
gdzie:
obliczeniowy współczynnik rezerwy plastycznej przekroju przy zginaniu
W- wskaźnik wytrzymałości przekroju przy zginaniu sprężystym
wskaźnik przekroju dla skrajnej krawędzi rozciąganej
a) dla przekrojów klasy 1 lub 2 
;
Gdzie:
współczynnik rezerwy plastycznej przy zginaniu.
b) dla przekrojów klasy 3 
2) dla przekrojów klasy 4 
lecz gdy 
gdzie:
współczynnik wpływu niestateczności miejscowej na niestateczność ogólną 
-współczynnik niestateczności miejscowej przy zginaniu
Nośność elementów zginanych jednokierunkowo należy sprawdzić według wzoru: 
Gdzie:
M - moment zginający od obciążeń o wartościach obliczeniowych.
nośność obliczeniowa przekroju przy zginaniu
współczynnik zwichrzenia.
gdy element jest dostatecznie zabezpieczony przed zwichrzeniem belek, może wystąpić utrata niestateczności lub gdy jest zginany względem osi, najmniejszej bezwładności przekroju.
Smukłość względną zwichrzenia 
elementów bisymtetrycznych o przekroju dwuteowym, swobodnie podpartych w sposób przybliżony ze wzoru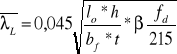 
gdzie;
długość - rozpiętość belki lub 
przy usztywnieniu stężeniami bocznymi
h - wysokość dwuteownika
szerokość pasa dwuteownika
współczynnik zależny od kształtu wykresu momentu zginającego ( odczytujemy z normy)
t -średnia grubość półki dwuteownika
Smukłość 
ceowników walcowych podpartych i obciążonych jak wyżej można wyznaczyć ze wzoru:
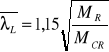
gdzie:
obliczeniowa nośność przy zginaniu
moment krytyczny przy zwichrzeniu
NOŚNOŚĆ ELEMENTÓW ŚCISKANYCH MIMOŚRODOWO (ściskanych i zginanych).
Nośność elementów mimośrodowo ściskanych o przekroju monosymetrycznym lub bisymetrycznym należy sprawdzić według wzoru: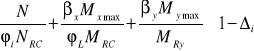 
gdzie:
N- siła ściskająca podłużna o wartości obliczeniowej.
-maksymalny moment zginający względem osi x oraz osi y.
są to współczynniki korekcyjne zależne od kształtu, wykresu momentu zginającego, odpowiednio w płaszczyznach x-x i y-y.
współczynnik wyboczeniowy pręta ściskanego osiowo
współczynnik zwichrzenia pręta zginającego.
obliczeniowa nośność przekroju przy ściskaniu
obliczeniowa nośność przekroju przy zginaniu jednokierunkowym, odpowiednio względem osi x lub y
składnik poprawkowy.
Jeżeli współczynnik 
nie odpowiada największej smukłości pręta, należy dodatkowo sprawdzić warunek 
gdzie:
- współczynnik odpowiadający największej smukłości pręta.
Jeżeli współczynniki korekcyjne 
zmniejszają wartość momentu zginającego (czyli 
) to należy dodatkowo sprawdzić warunek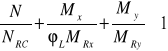 
.
Gdy w prętach mimośrodowo ściskanych występuje duża siła poprzeczna 
to należy sprawdzić warunek:
1) 
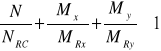
2) 
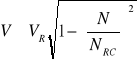
gdzie;
- są to zredukowane nośności przekroju przy zginaniu jednokierunkowym, względem odpowiednio osi x i y.