Realna wartość kapitału

Przykład

Kwotę 100 zł umieszczono jako roczną lokatę oprocentowaną w wysokości r = 11%. Inflacja w ciągu roku wyniosła i = 10%. Ile (naprawdę) zarobiliśmy?

Kwota 100 zł jest kapitałem zwiększonym, bo oprocentowanie odpisujemy po roku. Zatem jej wartość w momencie dopisywania odsetek wynosi:

Zatem po oprocentowaniu r = 11% mamy:

Zatem:

Załóżmy, że dany jest kapitał K₀. Załóżmy, że jego oprocentowanie w pewnym okresie czasu jest równe r. Załóżmy, ze w tym samym okresie stopa inflacji wynosi i (czyli kapitalizacja jest zgodna z okresem stopy inflacji).

Zatem po upływie tego okresu sytuacja wygląda następująco:

Po okresie kapitalizacji wartość naszego kapitału wynosi:

bo K₀ jest po okresie powiększony o odsetki, ale stracił na wartości z uwagi na inflację i zatem wartość, od której należy liczyć odsetki wynosi
; tzn. taka jest wartość kapitału K'₀ od którego liczymy odsetki
(K₀ - pełni tu rolę kapitału zwiększonego a K'₀ - kapitału podstawowego). Zatem po uwzględnieniu inflacji i tak jakbyśmy na początku mieli kapitał
.

Zatem jego realna wartość wynosi:

a liczbę

nazywamy wartością nominalną kapitału po okresie kapitalizacji.

Zatem mamy:

Twierdzenie:

Jeśli okres stopy procentowej r jest rόwny okresowi inflacji i to realna (rzeczywista) stopa procentowa wyraża się wzorem:

Wniosek

Jeśli stopa inflacji wynosi i, a realna stopa procentowa wynosi r_re to wartość stopy procentowej w tym samym okresie wyraża się wzorem:

Przykład

Jeśli w jakimś okresie stopa inflacji wynosi i = 0,03 = 3%, a nominalne oprocentowanie wynosi r = 0,04 = 4%, to rzeczywista stopa wzrostu kapitału wynosi:

Wniosek

1. Realna wartość kapitału rośnie <=> r > i

2. Realna wartość kapitału maleje <=> r < i

3. Realna wartość kapitału nie zmienia się <=> r = i

Z uwagi na inflację wprowadza się następujące pojęcie:

Definicja:

Waloryzację (indeksację) kapitału K₀ o wskaźnik inflacji i nazywamy kapitał K₀(1 + i).

Definicja ta wynikła z zależności

r- będzie równe rzeczywistemu powiększeniu kapitału jeśli zamiast K₀ przyjmiemy K₀(1 + i) (widać to, jeśli r = 0 - wówczas kwota nie zmieni się jeśli zamiast K₀ przyjmiemy K₀(1 + i))

Załóżmy teraz, że kapitalizacja jest niezgodna z okresem stopy inflacji i (zatem również niezgodna z okresem stopy procentowej r, który jest równy okresowi inflacji i). Załóżmy w okresie stopy inflacji (= stopie procentowej) odsetki są dopisywane m-razy. Wówczas realna wartość kapitału wynosi:

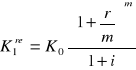
(Używamy wzoru na kapitalizację złożoną z dołu niezgodną po m okresach; tzn. K₁^re=K_m/m)

Wzór ten wynika z rozumowania analogicznego jak dla kapitalizacji zgodnej.

Twierdzenie

Jeśli okres stopy procentowej r jest równy okresowi stopy inflacji i, to przy m-krotnym dopisywaniu odsetek w okresie stopy inflacji i realna (rzeczywista) efektywna stopa procentowa wyraża się wzorem:

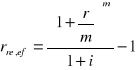
[było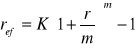
]

Dowód:

Oczywisty, bo:

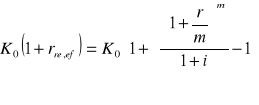
Wniosek:

Dowód:

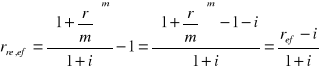
Załóżmy teraz, ze dokonujemy kapitalizacji kapitału K₀ przez n okresów. Załóżmy, że:

Przez n₁ okresów inflacja wynosiła i₁

Przez n₂ okresów inflacja wynosiła i₂

.

:

Przez n_m okresów inflacja wynosiła i_m

Niech n = n₁+n₂+ ... +n_m

Zatem w ciągu n okresów ceny wzrosły o czynnik

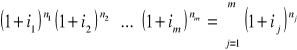
Wniosek:

W ciągu n-okresów stopa inflacji wynosi:

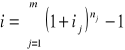
Dowód:

Oczywisty, bo dla kapitału K₀ mamy:

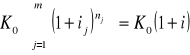
Zatem realna wartość kapitału K₀ po n okresach wynosi:

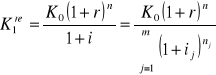
Możemy stąd zdefiniować (przy powyższych warunkach)

Definicja:

Przeciętną stopą inflacji nazywamy liczbę i_prz (albo
) taką, że:

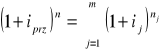
lub równoważnie: Przeciętną stopą inflacji nazywamy liczbę

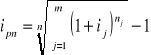
Dalej będzie o kapitalizacji ciągłej.

Kapitalizacja ciągła

Rozważmy kapitalizację złożoną niezgodną w podokresach. Niech będzie to model kapitalizacji z dołu. Niech liczba okresów kapitalizacji będzie wielokrotnością okresu stopy procentowej. Wówczas, jak wiemy:

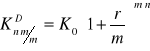
Rozważmy sytuację, gdy liczba podokresów kapitalizacji dąży do ∞, zatem są one coraz mniejsze. Wówczas mamy:

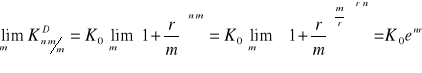
Definicja:

Kapitalizacja, dla której liczba podokresów dąży do nieskończoności nazywamy kapitalizacją ciągłą.

Wniosek:

Przyszła wartość kapitału K₀ po n okresach stopy procentowej r w modelu kapitalizacji ciągłej wyraża się wzorem:

Twierdzenie

Jeśli
jest kapitalizacją złożoną niezgodną z góry to

Dowód

Policzmy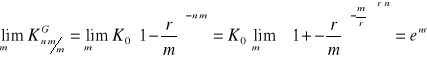
; co kończy dowód.

Wniosek

Kapitalizacja ciągła K(n) jest wspólną granicą ciągu
i ciągu
przy liczbie podokresów dążących do nieskończoności okresy stopy procentowej r możemy ustalać jako dowolne liczby rzeczywiste dodatnie t. Mamy wówczas do czynienia z modelem ciągłym kapitalizacji ciągłej, tzn.
; gdzie t > 0, t - oznacza czas oprocentowania mierzony okresem stopy procentowej r.

Niech dana będzie kapitalizacja złożona z dołu. Pamiętamy, że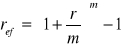
. Załóżmy, że rośnie liczba okresów m, i załóżmy, że r_ef jest takie samo dla wszystkich okresów. Wówczas nominalna stopa procentowa wynosi:

Twierdzenie

Dowód

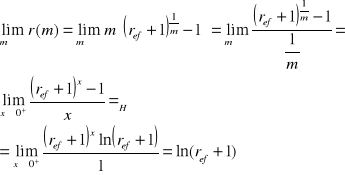
Definicja

Niech liczba kapitalizacji dąży do nieskończoności. Niech r_ef - jest efektywną stopą procentową w kapitalizacji złożonej z dołu. Intensywnością oprocentowania nazywamy liczbę:
.

Twierdzenie

Dla kapitalizacji złożonej z dołu w modelu ciągłym i przy stałym oprocentowaniu efektywnym r_ef mamy: K_t = K(t) = K₀e^{σ t}

Dowód

Mamy: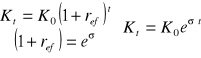
.

Zatem intensywność oprocentowania możemy interpretować jako nominalną stopę procentową w kapitalizacji ciągłej.

Uwaga

Intensywność oprocentowania σ dobrze przybliża nominalną stopę procentową dla dużych wartości m (np. dla m = 365; bo
)

Niech dana będzie teraz kapitalizacja złożona z góry.

Wówczas: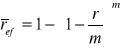
.

Załóżmy, że liczba okresów kapitalizacji m rośnie do nieskończoności i załóżmy, że
jest stała dla wszystkich okresów. Wówczas nominalna stopa procentowa

Twierdzenie

Dowód

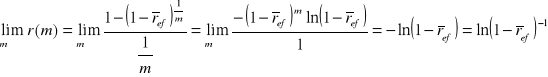
Zatem podobnie możemy zdefiniować:

Definicja

Niech liczba kapitalizacji dąży do nieskończoności. Niech
- efektywna stopa procentowa w kapitalizacji złożonej z góry. Intensywnością oprocentowania nazywamy liczbę
. Tutaj też mam
.

Było, że ciągi
są rosnące.

Zatem ciągi:

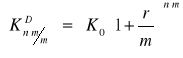
- rosnący, bo K₀ > 0

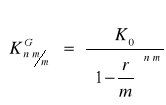
- malejący, bo K₀ > 0

Ponieważ kapitalizacja ciągła jest wspólną granicą obu ciągów, więc mamy:

Wniosek

Wszystkie kapitalizacje można dobrze przybliżać kapitalizacją ciągłą.

Jak przybliżać oprocentowanie?

1. Dla kapitalizacji złożonej z dołu:

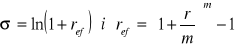
stąd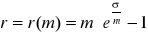

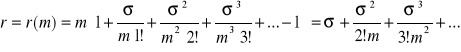
2. Dla kapitalizacji złożonej z góry

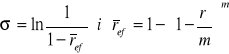
stąd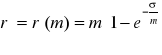

stąd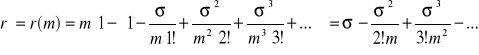

Oczywiście otrzymane szeregi są zbieżne dla każdego σ oraz

Rozwinięcia pokazują, jak można z dowolną dokładnością przybliżać r i r' przez σ.

---