RENTY

 

Renta jest to szereg płatności dokonywanych zawsze w jednakowej kwocie i w jednakowych odstępach czasu. Płatności w ramach renty nazywa się ratami odstęp czasu między poszczególnymi ratami nazywa się okresem bazowym.

Renty można pogrupować ze względu na:

Liczba  płatności: renty czasowe  (skończona ilość rat)  oznacza się wtedy przez A (ang. Annuites) oraz renty wieczyste (wypłacane bezterminowo) oznacza się przez P (ang. perpetuities).

Moment płatności: renty zwykłe (na koniec okresu) i renty należne na początek okresu.

Zgodność okresu bazowego z okresem kapitalizacji: renty proste okres bazowy pokrywa się z okresem kapitalizacji odsetek, renty efektywne okresy nie są zgodne.

Renta czasowa prosta.

Wartość renty można wyznaczyć wykorzystując wzory dla wartości przyszłej i bieżącej przepływów pieniężnych, wykorzystując założenia dotyczące rent.

 

Wartość przyszła renty zwykłej:

 

 ... ciąg geometryczny o wyrazie pierwszym
oraz ilorazie

Korzystając ze wzoru na sumę ciągu geometrycznego

 

podstawiając za
otrzymujemy wzór:

a po uproszczeniach

Wartość przyszła renty należnej

Różnica pomiędzy rentą zwykłą i należną polega na tym, że wszystkie raty przypadają o jeden okres wcześniej. W związku z tym, Wartość przyszłą należy liczyć ze wzoru:

Korzystając ze wzoru na sumę ciągu geometrycznego uzyskujemy:

Po uproszczeniach wzór można zapisać w postaci:

Wartość obecna renty zwykłej

Zgodnie z zasadami obliczania wartości obecnej przepływów pieniężnych:

Jest to suma ciągu geometrycznego o ilorazie
i wyrazie pierwszym
Zgodnie ze wzorem na sumę ciągu geometrycznego można zapisać:

Po uproszczeniach otrzymujemy wzór:

Wartość bieżąca renty należnej

Wzór na wartość bieżącą renty należnej można uzyskać w wyniku podobnych przekształceń jak w przypadku renty zwykłej

Jest to suma ciągu geometrycznego o ilorazie
i wyrazie pierwszym
Zgodnie ze wzorem na sumę ciągu geometrycznego można zapisać:

Po uproszczeniach otrzymujemy wzór:

Warto dodać , że przed podstawieniem do wzoru stopę procentową należy sprowadzić do okresu bazowego.

Przykład 1.

W nagrodę za dobre wyniki w nauce jeden ze sponsorów uczelni ufundował roczne stypendium płatne na koniec każdego miesiąca w wysokości 600 zł. Oblicz bieżącą i przyszłą wartość tego stypendium, jeżeli roczna stopa procentowa wynosi 6% a odsetki naliczane są co miesiąc.

Dane A=600 zł r _roczna =6% n=1 rok = 12 miesięcy.

Obliczamy wartość przyszłą renty zwykłej:

Obliczamy wartość obecną renty zwykłej:

Przykład 2.

Jaką kwotę należy wpłacać na początek każdego kwartału do funduszu inwestycyjnego aby po upływie 8 lat zgromadzić kwotę 20000 zł ? Stopa zwrotu tego funduszu jest stała i wynosi 8% rocznie, a od każdej wpłaty fundusz pobiera opłatę 3%.jak zmieni się wielkość raty, jeżeli byłaby ona płatna na koniec każdego kwartału.

Dane:

Liczba rat w rencie czasowej prostej

Dla renty czasowej zwykłej

Ze wzoru
należy wyliczyć n

dalej

dalej
stąd

ostatecznie:

Dla renty czasowej należnej analogicznie ze wzoru

należy

wyliczyć n

dalej

dalej
logarytmujemy obustronnie

ostatecznie

Renta dożywotnia prosta

Wartość przyszła renty dożywotniej prostej dąży do nieskończoności, możliwe jest natomiast ustalenie wartości obecnej takiej renty (PVP) Należy w tym celu wyznaczyć granicę przy n dążącym do nieskończoności.

Renta dożywotnia należna

Kredyty

Zaciągnięcie kredytu wiąże się z koniecznością terminowej, najczęściej comiesięcznej spłaty rat kapitałowych wraz z odsetkami. Najczęściej banki pobierają też prowizję za udzielenie kredytu. Poza tym, zwłaszcza przy większych kwotach banki żądają ubezpieczenia kredytu. Jest to zazwyczaj stała kwota wyznaczona jako procent wartości kredytu zwiększająca ratę kredytu.

Plan spłaty kredytu

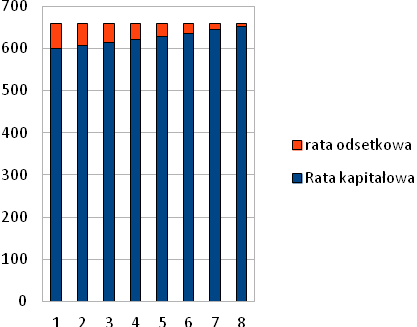
Raty kredytowe składają się zwykle z dwóch części raty kapitałowej i raty odsetkowej. Rata kapitałowa to część raty którą spłacamy kredyt czyli zmniejsza nasz dług w banku. Rata odsetkowa zawiera naliczone za dany miesiąc odsetki. Banki stosują dwa typy rat kredytowych : raty malejące i raty równe.

Raty malejące

Kredyt spłacany ratami malejącymi oznacza, że raty maleją z miesiąca na miesiąc. Wynika to ze stałej raty kapitałowej i malejącej raty odsetkowej (odsetki naliczane są od malejącego kapitału)

W tym wypadku łatwo jest wyznaczyć ratę kapitałową.

Przykład. Mamy kredyt 12000 zł z oprocentowaniem rocznym 12,99%. Sporządzić plan spłaty kredytu.

Raty równe

Raty kredytowe są jednakowe w każdym okresie spłaty (najczęściej miesiącu). Ponieważ raty odsetkowe maleją więc raty kapitałowe rosną.

Aby wyznaczyć ratę kredytową w przypadku kredytu spłacanego w równych ratach należy skorzystać ze wzoru na wartość bieżącą renty zwykłej.

Przykład2

Wyznaczyć miesięczną ratę kredytową oraz sporządź plan sp-łaty kredytu na kwotę 5000 zł, zakładając, okres spłaty w równych ratach przez 8 miesięcy, gdy oprocentowanie w skali roku wynosi 14,5%.

r=14,5% n=8

Ratę kredytu wyznaczamy z równania:

po obliczeniach otrzymujemy A=659,46 zł

Obliczanie planu spłaty

---