32. Fala elektromagnetyczna, światło spolaryzowane.

Promieniowanie elektromagnetyczne (fala elektromagnetyczna) - rozchodzące się w przestrzeni zaburzenie pola elektromagnetycznego. Zaburzenie to ma charakter fali poprzecznej, w której składowa elektryczna i magnetyczna są prostopadłe do siebie a obie są prostopadłe do kierunku rozchodzenia się promieniowania. Oba pola indukują się wzajemnie - zmieniające się pole elektryczne wytwarza zmienne pole magnetyczne, a zmieniające się pole magnetyczne wytwarza zmienne pole elektryczne. Źródłem pola EM jest poruszający się ładunek elektryczny. Gdy ładunek jest przyspieszany, jest emitowane promieniowanie elektromagnetyczne. Najczęściej źródłem tego promieniowania jest ładunek wykonujący drgania.

Podstawy teoretyczne

Spektrum fal elektromagnetycznych

1. Istnienie fali elektromagnetycznej przewidział James Clerk Maxwell w roku 1861.

2. Pierwszej emisji i odbioru fal elektromagnetycznych dokonał Heinrich Hertz w roku 1887.

Z równań Maxwella w przestrzeni nie zawierającej ładunków (w próżni) wynika:

gdzie

H - natężenie pola magnetycznego,

E - natężenie pola elektrycznego

Równania te są liniowymi równaniami różniczkowymi fali rozchodzącej się z prędkością
. Gdzie:
to przenikalność elektryczna, a μ to przenikalność magnetyczna. W próżni prędkość ta osiąga wartość

Gdzie przenikalności z indeksem 0 odnoszą się do próżni. Rozwiązaniem różniczkowych równań Maxwella są równania fali biegnącej. Dla fali płaskiej rozchodzącej się w kierunku x równania te mają postać:

gdzie

E₀ - amplituda natężenia pola elektrycznego,

H₀ - amplituda natężenia pola magnetycznego,

ν - częstotliwość fali elektromagnetycznej,

λ - długość fali.

Równania Maxwella i ich rozwiązanie pozwoliło połączyć pole elektryczne i magnetyczne w jedno pole elektromagnetyczne i pokazało bezpośredni związek tego pola ze światłem.

3. Promieniowanie elektromagnetyczne, choć jest falą, jak wynika z równań Maxwella, jest równocześnie strumieniem kwantów - fotonów. Im mniejsza długość fali, tym bardziej ujawnia się cząsteczkowa natura promieniowania elektromagnetycznego. Energia kwantu zależy od długości fali zgodnie ze wzorem:

.

Własności promieniowania

Promieniowanie elektromagnetyczne rozchodząc się objawia swe własności falowe zachowując się jak każda fala, ulega interferencji, dyfrakcji, spełnia prawo odbicia i załamania.

Rozchodzenie się fali w ośrodkach silnie zależy od ośrodków oraz częstotliwości fali. Fala rozchodząc się w ośrodku pobudza do drgań cząsteczki, atomy i elektrony zawarte w ośrodku, które są źródłami fal wtórnych, zmieniając tym samym warunki rozchodzenia się fali w stosunku do próżni.

Powstawanie i pochłanianie promieniowania elektromagnetycznego wiąże się ze zmianą ruchu ładunku elektrycznego.

Własności promieniowania elektromagnetycznego silnie zależą od długości fali (częstotliwości promieniowania) i dlatego dokonano podziału promieniowania elektromagnetycznego ze względu na jego częstotliwość.

Widmo fal elektromagnetycznych [

Widmo fal elektromagnetycznych A - fale radiowe bardzo długie, B - fale radiowe, C - mikrofale, D - podczerwień, E - światło widzialne, F - ultrafiolet, G - promieniowanie rentgenowskie, H - promieniowanie gamma, I - widmo światła widzialnego

Fale elektromagnetyczne zależnie od długości fali (częstotliwości) przejawiają się jako (od fal najdłuższych do najkrótszych):

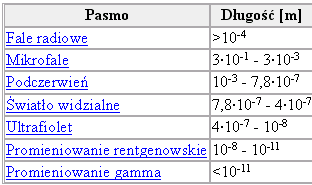
Granice poszczególnych zakresów promieniowania elektromagnetycznego są umowne i nieostre. Dlatego promieniowanie o tej samej długości może być nazywane falą radiową lub mikrofalą - w zależności od zastosowania. Graniczne promieniowanie gamma i promieniowanie rentgenowskie rozróżnia się z kolei ze względu na źródło tego promieniowania. Najdokładniej określone są granice dla światła widzialnego. Są one zdeterminowane fizjologią ludzkiego oka.

Polaryzacja to własność fali poprzecznej (np. światła). Fala spolaryzowana oscyluje tylko w pewnym wybranym kierunku. Fala niespolaryzowana oscyluje we wszystkich kierunkach jednakowo. Fala niespolaryzowana może być traktowana jako złożenie wielu fal drgających w różnych kierunkach.

W naturze większość źródeł promieniowania elektromagnetycznego wytwarza fale niespolaryzowane. Polaryzacja występuje tylko dla fal rozchodzących się w ośrodkach, w których drgania ośrodka mogą odbywać się w dowolnych kierunkach prostopadłych do rozchodzenia się fali. Ośrodkami takimi są trójwymiarowa przestrzeń lub struna.

Gdy ośrodek fali nie może drgać w dowolnych kierunkach prostopadłych względem rozchodzenia się fali zjawisko polaryzacji jest niemożliwe. Dotyczy to np.: drgań na powierzchni membrany i na granicach faz. Przykładem tego są m.in. fale morskie. Fale dźwiękowe również nie podlegają zjawisku polaryzacji, bo są falami podłużnymi.

Podstawy: fale płaskie [edytuj]

Najłatwiej jest sobie wyobrazić polaryzację płaskich fal sinusoidalnych. W większości przypadków światło to fale płaskie. Płaska fala elektromagnetyczna cechuje się tym, że wektory pola magnetycznego oraz elektrycznego prostopadłe do siebie leżą w jednej płaszczyźnie prostopadłej do kierunku propagacji fali, wektory te są zależne od siebie i podanie jednego jednoznacznie określa drugi dlatego przyjmuje się, że polaryzacja światła to zjawisko związane wyłącznie z wektorem pola elektrycznego. Wektor ten można rozłożyć na dwie składowe prostopadłe do siebie. Zmiany tych składowych można opisać funkcjami sinusoidalnymi, a zatem wystarczy podać ich fazę, amplitudę oraz częstotliwość, aby je jednoznacznie zdefiniować, przy czym obie składowe wektora pola elektrycznego zawsze mają taką samą częstotliwość, która odpowiada częstotliwości analizowanej fali elektromagnetycznej.

Rodzaje polaryzacji [edytuj]

Umieszczone tutaj ilustracje przedstawiają zmiany położenia punktu dla fali mechanicznej lub wektora pola elektrycznego dla fali elektromagnetycznej (niebieski) w czasie oraz jego składowych rzutowanych na dwie prostopadłe osie (czerwony/lewy oraz zielony/prawy) ustawione pod kątem prostym do płaszczyzny czoła fali. Na dole każdego wykresu kolorem fioletowym oznaczono ruch elementu drgającego.

Schemat polaryzacji liniowej

Schemat polaryzacji kołowej

Schemat polaryzacji eliptycznej

Przypadek po lewej, to polaryzacja liniowa, drganie odbywa się wzdłuż linii prostej. Każde drganie można przedstawić jako sumę drgań wzdłuż osi X i Y. W przypadku polaryzacji liniowej drgania składowe są w fazie lub w przeciwfazie (180°). Stosunek amplitud drgań składowych określa kierunek drgania a tym samym i polaryzację. Brak jednej ze składowych odpowiada polaryzacji wzdłuż osi. W polaryzacji liniowej przemieszczenie (natężenie pola elektrycznego) punktu w każdym cyklu przechodzi dwa razy przez zero.

Przypadek środkowy ilustruje polaryzację kołową. Drganie to odpowiada ruchowi po okręgu. Można je rozłożyć na dwa drgania o jednakowych amplitudach ale o fazach przesuniętych dokładnie o 90° lub 270° (-90°). W zależności do tego, czy fazy są przesunięte o 90° czy 270°, mówi się o polaryzacji kołowej prawoskrętnej lub polaryzacji kołowej lewoskrętnej. Wynika to z faktu, że wektor wychylenia może obracać się albo w lewo albo w prawo. W polaryzacji kołowej przemieszczenie (natężenie pola elektrycznego) ma zawsze taką samą wartość, zmienia się tylko kierunek przemieszczenia.

Trzeci rysunek przedstawia polaryzację eliptyczną, która jest uogólnieniem polaryzacji kołowej. Ruch ciała wytwarzającego drganie odbywa się po elipsie. Drganie to rozkłada się, podobnie jak w polaryzacji kołowej, na drgania o fazie przesuniętej o 90° lub 270° ale drgania składowe mają różne amplitudy. Polaryzacja eliptyczna może być wyrażona jako złożenie polaryzacji liniowej i kołowej.

Opis matematyczny [edytuj]

Równanie fali poprzecznej rozchodzącej się wzdłuż osi Z oraz wywołane nią drganie w wybranym punkcie (z=0) mogą być opisane wzorami:

• 
  - to odpowiednio wersory osi X i Y określające kierunek drgań,

• A_x,A_y - amplitudy drgań w wyznaczonych kierunkach,

• φ_x,φ_y - przesunięcia fazowe drgań.

Jeżeli φ_x = φ_y lub φ_x = φ_y + / − π to drgania te można przedstawić jako drgania
co odpowiada polaryzacji liniowej w kierunku v (rys. 1).

Jeżeli
oraz A_x = A_y = A to bez uwzględniania fazy początkowej drgania można opisać równaniem
. Równanie to jest równaniem okręgu i oznacza polaryzację kołową (rys. 2).

W ogólnym przypadku, gdy składowe mają różne amplitudy, wypadkowy ruch jest elipsą, stan ten opisuje pierwsze z przytoczonych równań, będące parametrycznym równaniem elipsy, a taki stan polaryzacji jest polaryzacją eliptyczną (rys. 3).

31 Równanie soczewki , konstrukcja obrazu dla soczewki skupiającej

Odległością przedmiotu i obrazu od soczewki spełnia zależność zwaną równaniem soczewki.

Wprowadźmy oznaczenia:

x - odległość przedmiotu od soczewki
y - odległość obrazu przedmiotu od soczewki
f - ogniskowa soczewki (odległość ogniska od środka soczewki)

Wtedy równanie soczewki wyrazi się wzorem:

Powyższe równanie soczewki obowiązuje wynika z modelu wprowadzonego dla soczewki idealnej. Rzeczywiste soczewki też oczywiście mają ognisko i (z pewną dokładnością spełniają to równanie). Warto jednak wiedzieć, że rzeczywiste soczewki mogą wykazywać dodatkowe efekty, które nie mieszczą się w powyższej zależności. Efekty te związane są głównie z faktem, że prawdziwe ognisko soczewki nigdy nie jest geometrycznym punktem. Związane jest to z różnym sposobem załamywania promieni o różnych kolorach, a także przechodzącymi dalej i bliżej osi optycznej soczewki. Więcej informacji na ten temat znajduje się w rozdziałach Aberracja chromatyczna, Aberracja sferyczna.

Konstrukcja obrazu dla soczewki

Na obraz przedmiotu składają się z obrazy poszczególnych punktów. Aby znaleźć położenie obrazu wytworzonego przez cienką soczewkę, wystarczy znaleźć obraz jednego punktu przedmiotu, który nie leży na osi optycznej. Do tego celu należy określić bieg dwóch dowolnych promieni wychodzących z tego punktu. Te dwa promienie można wybrać z trzech, które jest najłatwiej narysować:

Promień biegnący równolegle do osi, po przejściu przez soczewkę, przecina ognisko za soczewką (lub jego przedłużenie przecina ognisko dla soczewki rozpraszającej) - promień górny na rysunku.

1. Promień przechodzący przez pierwsze ognisko, lub leżący na prostej przechodzącej przez pierwsze ognisko, jest za soczewką równoległy do osi optycznej - promień dolny.

2. Promień przechodzący przez środek soczewki nie zmienia kierunku (dla soczewki doskonale cienkiej, dla rzeczywistych soczewek ulega niewielkiemu przesunięciu równoległemu) - promień środkowy.

Wiedząc, że obraz przedmiotu jest podobny do samego przedmiotu, co oznacza, że można go otrzymać przez translację, obrót i przeskalowanie z zachowaniem proporcji, można określić dokładne położenie obrazu.

30. Kąt padania, kat odbicia, kąt załamania związek pomiędzy nimi

Załamanie:

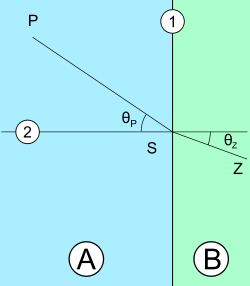
Zgodnie ze schematem promień P pochodzący z Ośrodka 1 w punkcie S załamuje się na granicy ośrodków i podąża jako promień Z w Ośrodku 2. Kąt padania oraz kąt załamania określa się między odpowiednim promieniem, a prostopadłą do granicy ośrodków w punkcie padania S, można oznaczyć kąt padania θ_P oraz kąt załamania θ_Z. Sinusy tych kątów wiąże następująca zależność:

,

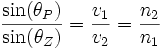
gdzie:

v_i prędkość fali w ośrodku i,

n₁- współczynnik załamania światła ośrodka 1,

n₂- współczynnik załamania światła ośrodka 2.

Optyka w miejsce prędkości fal świetlnych posługuje się współczynnikami załamania. Prawo załamania zostało doświadczalnie odkryte przez Willebrorda Snella i nazywane jest prawem Snella lub Snelliusa. Prawo to można wyprowadzić z zasady Fermata lub zasady Huygensa.

Załamanie światła na granicy próżni - ośrodek

Bardziej złożony przykład refrakcji światła przez szkło

Przyjmując ośrodek 1 jako próżnię i oznaczając prędkość światła jako c, to prędkość światła w ośrodku o współczynniku załamania n_op opisuje zależność:

gdzie:

• v_o - prędkość światła w ośrodku,

• c - prędkość światła w próżni,

• n_op - współczynnik załamania światła (współczynnik refrakcji) ośrodka względem próżni.

Zmiana długości fali

Przejście fali elektromagnetycznej z próżni do ośrodka powoduje zmianę długości fali zgodnie z zależnością:

gdzie:

• λ_o - długość fali w ośrodku,

• λ - długość fali w próżni

• Odbicie to nagła zmiana kierunku rozchodzenia się fali na granicy dwóch ośrodków powodująca, że pozostaje ona w ośrodku, w którym się rozchodzi. Odbicie może dawać obraz lustrzany lub być rozmyte, zachowując tylko właściwości fali, ale nie dokładny obraz jej źródła.

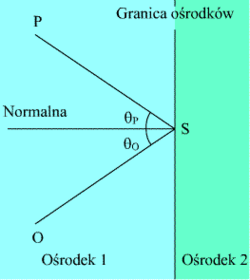
Odbicie zwierciadlane

Odbicie zwierciadlane może mieć miejsce na gładkiej powierzchni oddzielającej dwa różne materiały, np. lustro wody albo metalizowana powierzchnia. Zgodnie ze schematem Promień świetlny P zwany promieniem padającym pada w punkcie S na granicę ośrodków i odbija się jako promień odbity O.

Prostopadła do powierzchni odbijającej w punkcie padania promienia zwana jest normalną padania.

Kąt padania to kąt między promieniem padającym a normalną do powierzchni (osią prostopadłą do powierzchni) θ_P.

Kąt odbicia to kąt między promieniem odbitym a normalną do powierzchni (osią prostopadłą do powierzchni) θ_O.

Prawo odbicia

Kąt odbicia jest równy kątowi padania, a promień padający, promień odbity i normalna leżą w jednej płaszczyźnie. W wyniku odbicia zmienia się tylko kierunek rozchodzenia się fali, nie zmienia się jej długość.

Zwierciadło

Urządzenie zbudowane w celu odbijania fal to zwierciadło.Aby zaszło odbicie ośrodki muszą mieć różne współczynniki załamania. W szczególnym przypadku możliwe jest całkowite wewnętrzne odbicie fali od powierzchni oddzielającej różne materiały.

29. Fala elektromagnetyczna(długość okres częstotliwość )

Fala - to rozchodzące się w przestrzeni, zależne od czasu, zaburzenie.

http://www.iwiedza.net/wiedza/115.html

Elektromagnetyzm jest działem fizyki obejmującym zagadnienia współzależności zjawisk magnetycznych i elektrycznych, np. wytwarzanie pola magnetycznego za pomocą prądu elektrycznego. Elektromagnetyzm może być wykorzystany na dwa sposoby. Pierwszy z nich to zjawisko indukcji elektromagnetycznej, która zachodzi wówczas, gdy magnes porusza się wewnątrz zwojnicy, wytwarzając w niej prąd elektryczny. Drugim sposobem jest siła elektrodynamicza. Powstaje wówczas, gdy przewód, w którym płynie prąd, jest umieszczony między biegunami magnesu.

Promieniowanie elektromagnetyczne

Promieniowanie jest aktem emisji strumieni cząstek (fotonów, elektronów, neutronów) emitowanych przez układy materialne (cząsteczki, atomy, jądra atomowe).
Promieniowanie elektromagnetyczne (fotonowe) jest emitowane wskutek zmian zachodzących wewnątrz jądra atomowego lub poprzez wzbudzone atomy i cząsteczki, w wyniku anihilacji (zamiany) pary elektron-pozyton na kwant pola elektromagnetycznego, w tym wypadku na dwa fotony tegoż promieniowania.

Promieniowanie elektromagnetyczne rozchodzi się w postaci fal elektromagnetycznych, których widmo (spectrum) przedstawia rysunek. Nazwy nadane różnym obszarom tego widma związane są z odpowiednimi eksperymentalnymi technikami wytwarzania i wykrywania tych fal.
Zjawiska dyfrakcji i interferencji promieni elektromagnetycznych świadczą o falowym charakterze promieniowania elektromagnetycznego, zaś zjawisko fotoelektryczne przemawia za korpuskularną strukturą promieniowania elektromagnetycznego. W pewnych przypadkach promieniowanie elektromagnetyczne zachowuje się więc jak fala o określonej częstotliwości ν i długości fali λ, a w innych rozchodzi się w postaci fotonów o określonej energii E, pędzie p oraz masie spoczynkowej równej zero. W związku z tymi faktami mówimy o dwoistej naturze lub o dualizmie korpuskularno-falowym promieniowania elektromagnetycznego. Możliwości przejścia między falowym a fotonowym obrazem dostarczają nam wzory

Fala elektromagnetyczna

Fala elektromagnetyczna to wzajemnie przenikające się drgania elektryczne i magnetyczne. Fala taka powstaje np. wtedy, gdy elektron w atomie traci energię i przeskakuje na orbitę bliżej jądra atomu. Powstają przy tym drgania elektryczne, które rozchodzą się w przestrzeni w postaci pola elektrycznego i magnetycznego. Pola te są prostopadłe do siebie i do kierunku rozchodzenia się fali. Pierwszym, który wprowadził pojęcie pola elektromagnetycznego był fizyk James Clerk Maxwell.

Cechą charakterystyczną fal elektromagnetycznych jest ich możliwość rozchodzenia się w próżni, czym w zasadniczy sposób różnią się od fal mechanicznych, które mogą się rozchodzić jedynie w ośrodkach sprężystych. Różni je także olbrzymia prędkość, z jaką się poruszają. Są to fale poprzeczne. Ich długość dana jest wzorem:

Podział fal elektromagnetycznych na poszczególne rodzaje dokonuje się ze względu na sposób ich wytwarzania. Fale radiowe czy mikrofale są wytwarzane sztucznie za pomocą przyrządów elektronicznych. Promieniowanie podczerwone świetlne i ultrafioletowe powstaje wskutek zmian energetycznych, zachodzących w elektronowej powłoce wewnętrznej atomów lub cząsteczek. Promienie X powstają przez hamowanie w polu kulombowskim jąder sztucznie wytworzonej wiązki rozpędzonych elektronów lub wskutek przejść energetycznych, zachodzących w wewnętrznej powłoce elektronowej atomów. Promieniowanie gamma powstaje przy przejściach energetycznych wewnątrz wzbudzonych jąder. Promieniowanie kosmiczne powstaje podczas hamowania elektronów lub innych cząstek elementarnych o dużej energii w kulombowskim polu jąder atomowych.

Wielkości fizyczne fali

Długość fali

Długością fali nazywamy odległość jaką przebywa fala w czasie jednego okresu. Kiedy nadchodzi fala o określonej częstotliwości, jej grzbiety znajdują się w równych odległościach od siebie. Odległość związana z jednym pełnym drganiem to długość fali. Fale o wyższej częstotliwości mają mniejszą długość fali. Fale o niższej częstotliwości mają większą długość fali.

Długość fali oznacza się grecką literą lamba (λ). Długość ta zależy od częstotliwości fali f i prędkości fali V. Zależność pomiędzy tymi wielkościami jest następująca:

gdzie T=1/f jest okresem drgań fali, czyli czasem, w którym podczas przechodzenia przez ośrodek fali sinusoidalnej, dana cząsteczka wykonuje jedno pełne drganie. Jednostką długości fali jest metr, co można łatwo sprawdzić, podstawiając za prędkość V - [m/s], a za częstotliwość f - [1/s].

Amplituda fali

Jest to maksymalne wychylenie cząstki z położenia równowagi. Amplituda fali to wysokość grzbietu lub głębokość doliny fali. Większa amplituda oznacza, że fala niesie więcej energii. Amplitudę zwykle oznaczamy dużą literą A, lub też poprzez zapis y_max .

Częstotliwość fali

Częstotliwość fali mówi o szybkości rozchodzenia się grzbietów fali. Jest to liczba pełnych drgań fali, od grzbietu do grzbietu, na jedną sekundę. Częstotliwość mierzymy w hercach (f=[Hz]=[1/s]). Jeden herc to jedno pełne drganie na sekundę. Dla przykładu fale radiowe UKF rozchodzą się z częstotliwością około 100 milionów herców. Nazwa tej jednostki pochodzi od nazwiska niemieckiego fizyka Heinricha Hertza.

Prędkość fali

Prędkość fal elektromagnetycznych (prędkość światła) jest największą prędkością znaną we Wszechświecie i wynosi ona w przybliżeniu około 300,000 km/s. Ta wielkość fizyczna jest bardzo ważna, gdyż świadczy o elektromagnetycznym charakterze danej fali. Po raz pierwszy prędkość światła została wyznaczona w 1673 roku przez Roemera. Korzystając z obserwacji astronomicznych ocenił on prędkość na około 200,000 km/s.
Poniżej przedstawiono schemat pomiaru prędkości światła metodą Michelsona

Wytworzone za pomocą łuku elektrycznego światło biegło pomiędzy dwoma szczytami, Mt. Wilson i Mt. San Antonio w Kalifornii, pokonując odległość L=(35410 ą 3)m. Padając na wirujący układ zwierciadeł, odbijało się od zwierciadła 1, przebywało drogę 2L i po odbiciu od zwierciadła 2, które w tym czasie znalazło się w miejscu zwierciadła 3, docierało do obserwatora. Znając częstotliwość z jaką wirował układ zwierciadeł oraz drogę L można było z dużą dokładnością wyznaczyć prędkość światła. Mierzona wówczas prędkość wyniosła c=(299796 ą 4) km/s.
Według ostatnich bardzo dokładnych, eksperymentalnych pomiarów, prędkość światła jest równa (299792458 ą 1,2) m/s.

Faza fali

Gdy przez pewien punkt przechodzą kolejno grzbiety i doliny fali, jej faza w tym punkcie zmienia się bez przerwy. Jeśli fale się dodają, istotna jest różnica faz. Gdy dwie fale o tej samej częstotliwości są w fazie, ich grzbiety nadchodzą zawsze razem. Powstaje wypadkowa fala o większej amplitudzie. Jest to zasada superpozycji. Jeżeli grzbiety jednej fali nadchodzą zawsze razem z dolinami drugiej, to fale są w przeciwfazie i mogą się wzajemnie całkiem zniwelować. Przy nakładaniu promieni świetlnych dostajemy jasny promień, gdy fale są w fazie i wygaszenie światła, gdy fale są w przeciwfazie. Na tym polega .

Fala czerwona i niebieska dodają się i powstaje fala żółta. Kiedy fale są w fazie, ich interferencja jest konstruktywna. Powstaje fala o wyższych grzbietach i głębszych dolinach. Kiedy dwie o tej samej amplitudzie są w przeciwfazie, ich interferencja jest destruktywna, to znaczy całkowicie się odejmują i nie ma żadnej fali.

Zjawiska falowe

O tym czy dana fala jest falą elektromagnetyczną świadczyć może fakt, jakim dana fala "poddaje" się zjawiskom falowym. W początkach wieku XIX panowała w nauce tzw. korpuskularna teoria światła. Według tej teorii światło polega na ruchu maleńkich ciałek, korpuskuł, wylatujących ze źródła światła i poruszających się po liniach prostych. Korpuskuły te, wpadając do oka, wywołują wrażenie światła. Dzisiaj wiadomo, że światło jest strumieniem małych porcji energii, zwanych fotonami, które zachowują się jednocześnie jak fale i jak cząstki. Jest to rodzaj fali elektromagnetycznej, która ulega zjawiskom dyfrakcji, interferencji i polaryzacji. W związku z tym, należałoby nieco przybliżyć zjawiska jakie charakteryzują także i fale elektromagnetyczne. Zjawiska te przeanalizujemy na przykładzie światła.

28 Różnica między ciepłem a temperaturą, ciepło właściwie, parowania i topnienia.

 "Ciepło jest to energia, jaką układ o wyższej temperaturze przekazuje znajdującemu się z nim w kontakcie cieplnym układowi o niższej temperaturze w procesie dochodzenia obu układów do stanu równowagi"

Temperatura - jedna z podstawowych w termodynamice wielkości fizycznych (parametrów stanu) ^[1], będąca miarą stopnia nagrzania ciał. Temperaturę można ściśle zdefiniować tylko dla stanów równowagi termodynamicznej, z termodynamicznego bowiem punktu widzenia jest ona wielkością reprezentującą wspólną własność dwóch układów pozostających w równowadze ze sobą. Temperatura jest związana ze średnią energią kinetyczną ruchu i drgań wszystkich cząsteczek tworzących dany układ i jest miarą tej energii.

Temperatura jest miarą "chęci" do dzielenia się ciepłem. Jeśli dwa ciała mają tę samą temperaturę, to w bezpośrednim kontakcie nie przekazują sobie ciepła, gdy zaś mają różną temperaturę, to następuje przekazywanie ciepła z ciała o wyższej temperaturze do ciała o niższej - aż do wyrównania się temperatur obu ciał.

Ciepło - w fizyce to jeden z dwóch sposobów, obok pracy, przekazywania energii układowi termodynamicznemu^[1] polega na przekazywaniu energii chaotycznego ruchu cząstek (atomów, cząsteczek, jonów) w zderzeniach cząstek tworzących te układy;^[2] oznacza formę zmian energii, nie zaś jedną z form energii.^[3]

Dla odróżnienia ciepła jako zjawiska fizycznego od ciepła jako wielkości fizycznej używa się określenia wymiana cieplna^[2] lub cieplny przepływ energii na określenie procesu, a ilość ciepła na wielkość fizyczną określającą zmianę energii wywołaną tym zjawiskiem.

Ciepło przepływa między ciałami, które nie znajdują się równowadze termicznej, tzn. gdy mają one różne temperatury i wywołuje zwykle zmianę temperatury.^[2] Ciała te muszą pozostawać ze sobą w kontakcie termicznym - musi istnieć możliwość przepływu ciepła.

Potocznie, przez ciepło rozumie się odczucie zadowolenia z przystosowania się organizmu do aktualnych warunków termicznych otoczenia. Naukowo to odczucie nazywa się komfortem cieplnym. Potoczne znaczenie słowa "ciepło" może być źródłem nieporozumień. Ponieważ w języku potocznym termin ten określa stan ciała, a w terminologii fizycznej - wielkość związaną z wymianą energii wewnętrznej. Stwierdzenie, że coś jest "cieplejsze" oznacza w języku fizyki, że ma wyższą temperaturę.

Ciepło właściwe (c) - energia termiczna potrzebna do podniesienia temperatury jednej jednostki masy ciała o jedną jednostkę temperatury. W układzie SI ciepło właściwe podaje się w dżulach na kilogram razy kelwin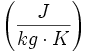
. Ciepło właściwe jest to wielkość, która charakteryzuje każdą substancję pod względem energetycznym.

Ciepło parowania - ilość energii potrzebnej do odparowania jednostki masy danej substancji, przy stałym ciśnieniu i temperaturze. W układzie SI jednostką ciepła parowania jest J/kg. Stosuje się też jednostkę J/mol.

Ciepło parowania zależy silnie od ciśnienia (temperatury) zmiany stanu skupienia, malejąc wraz ze wzrostem temperatury i osiągając 0 w punkcie krytycznym.

Jeżeli nie podano dla jakiego ciśnienia określono ciepło parowania, to uznaje się, że określono je dla ciśnienia atmosferycznego.

Ciepło topnienia jest to ilość energii potrzebnej do stopienia jednostki masy danej substancji. W układzie SI jednostką ciepła topnienia jest J/kg (dżul na kilogram).

gdzie:

• Q - ilość dostarczonego ciepła,

• m - masa ciała,

• q - ciepło topnienia.

27. Gaz doskonały ( związek pomiędzy p, V,T) , przemiany gazowe

Gaz doskonały - zwany gazem idealnym jest to abstrakcyjny, matematyczny model gazu, spełniający następujące warunki:

1. brak oddziaływań międzycząsteczkowych z wyjątkiem odpychania w momencie zderzeń cząsteczek

2. objętość cząsteczek jest znikoma w stosunku do objętości gazu

3. zderzenia cząsteczek są doskonale sprężyste

4. cząsteczki znajdują się w ciągłym chaotycznym ruchu

Założenia te wyjaśniły podstawowe właściwości gazów. Po odkryciu własności cząstek w mechanice kwantowej, zastosowano te założenia też do cząstek kwantowych. Powyższe założenia prowadzą do następujących modeli:

1. Klasyczny gaz doskonały,

2. Gaz Fermiego, będący zastosowaniem modelu do fermionów, np. elektronów w metalu

3. Gaz bozonów, będący zastosowaniem modelu do bozonów, np. fotonów.

Klasyczny gaz doskonały [edytuj]

Gaz taki w mechanice klasycznej opisuje równanie Clapeyrona (równanie stanu gazu doskonałego), przedstawiające zależność między ciśnieniem gazu (p), jego objętością (V), temperaturą (T) i licznością (n) wyrażoną w molach:

 gdzie  R jest stałą gazową

lub

 gdzie  k jest stałą Boltzmanna.

n = m/M jak wiadomo z chemii :) gdzie m to masa substacji, a M to masa molowe tej substancji. Zatem można zapisać jeszcze jedną postać tego równania:

Gaz doskonały to model, słuszny w pełni jedynie dla bardzo rozrzedzonych gazów. Wzrost ciśnienia powoduje, że zmniejszają się odległości między cząsteczkami oraz powoduje pojawianie się oddziaływań międzycząsteczkowych. Oddziaływania te występują też blisko temperatury skraplania. W bardzo wysokich temperaturach zderzenia przestają być sprężyste. Model ten może być jednak stosowany w praktyce do niemalże wszystkich gazów w warunkach normalnych. Dla gazów rzeczywistych przy dużych gęstościach i ciśnieniach niezbędne jest stosowanie równań uwzględniających te efekty (zob. równanie Van der Waalsa i wirialne równanie stanu).

Temperatura zera bezwzględnego - definicja
Jest to najniższa temperatura, do której możemy się zbliżać, ale jej osiągnięcie jest niemożliwe (ciśnienie i objętość musiałyby być równe zeru). W temperaturze tej zanika całkowicie ruch cząsteczek. Temperatura ta jest równa -273,15 ^oC lub 0 K (kelwinów).

Skala Kelvina nazywana jest również bezwzględną skalą temperatur. Jednostkowy przyrost temperatury w obydwu skalach jest taki sam:

Δt = 1^oC = 1K
T = t(^oC) + 273,15 T - temp. w kalwinach

PRZEMIANY GAZOWE

Dla wszystkich przemian prawdziwa jest zależność:

(p₁V₁)/T₁ = (p₁V₂)/T₂

czyli, innymi słowy stosunek iloczyny ciśnienia i objętości do temperatury gazu jest zawsze taki sam.

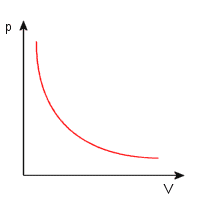
Przemiana izotermiczna jest nazywana również prawem Boyle'a - Mariotte'a. Jak sama nazwa wskazuje, w przemianie tej temperatura nie ulega zmianie:

T = const

w związku z tym również:

pV = const

  Wykres ten przedstawia zależność ciśnienia od   objętośći dla gazu w przemianie izotermicznej. Krzywa   ta nazywa się izotermą.

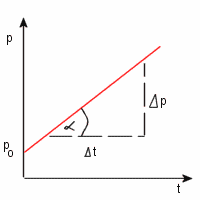
Przemiana izohoryczna stałej masy gazu charakteryzuje się niezmiennością objętości. Przyrost ciśnienia jest wprost proporcjonalny do przyrostu temperatury.

V = const

p / T = const

Równanie tej prostej, zwanej również izochorą można zapisać :

p = (Δp / Δt) ^. t + p₀

 

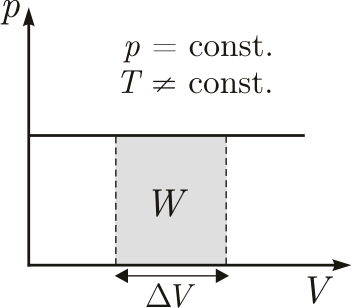
Przemiana izobaryczna zachodzi, gdy ciśnienie stałej masy gazu nie ulega zmianie. Przyrots objętości jest wprost proporcjonalny do przyrostu temperatury.

p = const

V / T = const

Równanie tej prostej zwanej izobarą można zapisać:

V = (ΔV / Δt) ^. t + V₀

26.Pole magnetyczne. (Prawo Biota-Savarta)

Pole magnetyczne w fizyce jest stanem (własnością) przestrzeni, w której siły działają na poruszające się ładunki elektryczne, a także na ciała mające moment magnetyczny niezależnie od ich ruchu. Pole magnetyczne jest obok pola elektrycznego przejawem pola elektromagnetycznego. W zależności od opisu (obserwatora), to samo zjawisko może być opisywane jako objaw pola elektrycznego, magnetycznego lub obu.

Pole magnetyczne jest polem wektorowym, wielkości fizyczne używane do opisu pola magnetycznego to indukcja magnetyczna B oraz natężenie pola magnetycznego H (te dwie wielkości są powiązane ze sobą poprzez przenikalność magnetyczną).

Obrazowo pole magnetyczne przedstawia się jako linie pola magnetycznego. Kierunek pola określa ustawienie igły magnetycznej lub obwodu, w którym płynie prąd elektryczny.

Stałe pole magnetyczne jest wywoływane przez ładunki elektryczne znajdujące się w ruchu jednostajnym. Dlatego też, przepływ prądu (który też jest ruchem ładunków elektrycznych) wytwarza pole magnetyczne. Ładunki poruszające się ruchem zmiennym (np. hamowane) wytwarzają zmienne pole magnetyczne, które rozchodzi się jako fala elektromagnetyczna. Wytwarzanie pola przez prąd i ładunki w ruchu opisuje Prawo Biota-Savarta, oraz prawo Ampera będące obecnie częścią równań Maxwella.

Niektóre materiały magnetyczne, jak np. ferromagnetyki, wykazują istnienie stałego pola magnetycznego. Jego istnienie spowodowane jest przez ruch ładunków elektrycznych głównie elektronów w atomach takiego materiału. Zjawisko to jest dokładniej wyjaśnione w opisie magnetyzmu.

Pole magnetyczne jest też wytwarzane przez zmienne pole elektryczne. Z kolei zmienne pole magnetyczne wytwarza pole elektryczne. Takie wzajemnie indukowanie się pól zachodzi w fali elektromagnetycznej. Stałe w czasie pole magnetyczne nie wytwarza pola elektrycznego, co także matematycznie ujmują równania Maxwella.

Własności pola magnetycznego [edytuj]

Pole magnetyczne jest bezźródłowe, co wyraża Prawo Gaussa dla magnetyzmu. Wynika z niego, że linie pola magnetycznego tworzą zamknięte krzywe, nie zaczynają się, ani się nie kończą.

Pole magnetyczne kołowe [edytuj]

Pole magnetyczne kołowe jest to przestrzeń, której linie pola magnetycznego układają się we współśrodkowe okręgi. Pole takie jest wytwarzane przez prostoliniowy przewodnik. Indukcja magnetyczna takiego pola jest większa bliżej źródła.

Definicja [edytuj]

Podobnie jak w polu elektrycznym pole magnetyczne definiuje się przez siłę, jaka działa na poruszający się ładunek w polu magnetycznym. W układzie SI siła ta wyraża się wzorem:

Gdzie:

to wektor siły

to iloczyn wektorowy

to ładunek elektryczny

to wektor prędkości ładunku

to wektor indukcji magnetycznej

W układzie Gaussa:

Wzór na siłę zapisany skalarnie:

gdzie α to kąt pomiędzy wektorem prędkości a indukcji magnetycznej

Pole magnetyczne jako konsekwencja szczególnej teorii względności [edytuj]

Pole magnetyczne będące składnikiem pola elektromagnetycznego jest różnie widziane w zależności od obserwatora. Wielkości pól elektrycznego i magnetycznego zależą od układu odniesienia obserwatora (transformata pola). Powstawanie pola magnetycznego w wyniku płynięcia prądu (ruchu ładunków) można tłumaczyć jako konsekwencję skrócenia przestrzeni dla poruszających się ładunków, skutkującą powstawaniem dodatkowej siły kulombowskiej pomiędzy ładunkami wzajemnie się poruszającymi. Zauważyć można, że pole magnetyczne jest nierozerwalnie związane z polem elektrycznym. Pole magnetyczne jest w istocie swego rodzaju "pomocniczym polem" w rozważaniach oddziaływań elektromagnetycznych. W rzeczywistości jest ono polem elektrycznym, pojawiającym się "dodatkowo" w odniesieniu do wzajemnie ruchomych ładunków jako konsekwencja szczególnej teorii względności Einsteina. Można by tak skonstruować prawa elektromagnetyzmu by nie było w nich pola magnetycznego, jednak byłoby to wysoce niewygodne w licznych teoretycznych i praktycznych zastosowaniach.

Prawo Biota-Savarta w fizyce prawo stosowane w elektromagnetyzmie i dynamice płynów. Oryginalna wersja została sformułowana dla pola magnetycznego.

W elektromagnetyzmie

Przewodnik z prądem

Przyczynek
do pola indukcji magnetycznej w danym punkcie A od elementu długości
przewodnika z prądem o natężeniu I.

gdzie

zwana stałą magnetyczną

- natężenie prądu, wyrażone w amperach

- skierowany element przewodnika; wektor o kierunku przewodnika, zwrocie odpowiadającym kierunkowi prądu i długości równej długość elementu przewodnika

- wersor dla punktów wytwarzającego pole (elementu przewodnika) i miejsca pola

- odległość elementu przewodnika od punktu pola.

Inna postać wzoru:

gdzie
to wektor wodzący o początku w źródle pola i końcu w rozważanym punkcie przestrzeni. Wartość indukcji magnetycznej może być obliczona ze wzoru

Rozciągły obszar z prądem

Wyżej przytoczony wzór jest prawdziwy dla cienkich przewodników z prądem, dla obszarów w których płynie prąd w dużych objętościach wzór przyjmuje postać:

gdzie:

- gęstość prądu

dV - element objętości

Poruszający się ładunek

gdzie:

q - ładunek elektryczny

- prędkość ładunku.

Pole w danym punkcie

Całkowitą indukcję magnetyczną wyznacza się całkując różniczkowe elementy indukcji
wzdłuż całego przewodnika - w pierwszym wzorze, a w całym obszarze, w którym płynie prąd w drugim wzorze.

Wnioski

Wzór Biota - Savarta umożliwia obliczenie indukcji magnetycznej gdy znane jest natężenie prądu, który jest źródłem pola magnetycznego (punkty tego pola są scharakteryzowane przez wektor indukcji, a wartość tego wektora określa wzór Biota - Savarta).

Wszystkie przyczynki do wektora indukcji pochodzące od elementów przewodnika mają w danym punkcie taki sam kierunek, który jest prostopadły do płaszczyzny w której leży przewodnik i analizowany punkt. Dlatego pole magnetyczne ma kształt okręgów leżących w płaszczyźnie prostopadłej do przewodnika, środkami których jest przewodnik, a indukcję magnetyczna określa wzór:

gdzie:

I - natężenie prądu

r - odległość od przewodnika.

25. Kondensatory (definicja łączenia kondensatorów)

Kondensator to element elektryczny (elektroniczny) zbudowany z dwóch przewodników (okładzin) rozdzielonych dielektrykiem (izolator elektryczny )

Działanie

Doprowadzenie napięcia do okładzin kondensatora powoduje zgromadzenie się na nich ładunku elektrycznego. Jeżeli kondensator jako całość nie jest naelektryzowany, to cały ładunek zgromadzony na jego okładkach jest jednakowy, ale przeciwnego znaku. Kondensator charakteryzuje pojemność określająca zdolność kondensatora do gromadzenia ładunku:

gdzie:

• C - pojemność, w faradach

• Q - ładunek zgromadzony na jednej okładce, w kulombach

• U - napięcie elektryczne między okładkami, w woltach.

Pojemność wyrażana jest w faradach. Jeden farad to bardzo duża jednostka, dlatego w praktyce spotyka się kondensatory o pojemnościach piko-, nano-, mikro- i milifaradów.

Szeregowe łączenie kondensatorów

Przy połączeniu szeregowym kondensatorów, odwrotność pojemności wypadkowej jest równa sumie odwrotności wszystkich pojemności składowych:

gdzie:
Cz - pojemność zastępcza (wypadkowa)
C1, C2, C3 - pojemności składowe

W praktyce bardzo często korzysta się ze wzorów uwzględniających tylko dwie lub trzy pojemności składowe:

Powyższe wzory można w bardzo prosty sposób zapamiętać: w liczniku umieszczamy iloczyn (mnożenie) wszystkich występujących pojemności, a w mianowniku sumę podwójnych kombinacji iloczynów składowych.

Równoległe łączenie kondensatorów

Przy połączeniu równoległym kondensatorów, pojemność wypadkowa jest równa sumie pojemności składowych: 

Cz = C1 + C2 + C3 ...

gdzie:
Cz - pojemność zastępcza (wypadkowa)
C1, C2, C3 - pojemności składowe

24. Pole elektryczne (prawo columba , strumień pola)

Pole elektryczne, jedna z postaci pola elektromagnetycznego; oddziaływanie między naładowanymi elektrycznie cząstkami lub ciałami, poruszającymi się w dowolny sposób względem inercjalnego układu odniesienia. Wywiera ono na ładunek elektryczny (naładowaną cząstkę lub ciało) siłę, która nie zależy od prędkości ruchu ładunku.

Pole elektryczne opisuje wektor natężenia pola elektrycznego E. Jest on równy stosunkowi siły F, jaką pole elektryczne wywiera na próbny ładunek punktowy, do wartości q tego ładunku:

E=F/q

Prawo Coulomba głosi, że siła wzajemnego oddziaływania dwóch punktowych ładunków elektrycznych jest wprost proporcjonalna do iloczynu tych ładunków i odwrotnie proporcjonalna do kwadratu odległości między ich środkami. Jest to podstawowe prawo elektrostatyki. Zostało ono opublikowane w 1785 roku przez francuskiego fizyka Charles'a Coulomba. Prawo to można przedstawić za pomocą wzoru:

,

w którym:

F - siła wzajemnego oddziaływania dwóch punktowych ładunków elektrycznych,

q₁ , q₂ - punktowe ładunki elektryczne,

r - odległość między ładunkami,

k - współczynnik proporcjonalności:

gdzie:

- względna przenikalność elektryczna ośrodka;

- przenikalność elektryczna próżni.

Kierunek działania siły oddziaływania ładunków wyznaczony jest przez prostą łączącą oba te ładunki, natomiast o zwrocie decydują znaki ładunków. Jeżeli są one jednoimienne, oddziaływanie jest odpychaniem. W przypadku ładunków różnoimiennych ładunki przyciągają się. Siłę oddziaływania ładunku B na ładunek A można przedstawić wzorem wektorowym:

gdzie poszczególne wielkości pokazane są na rysunku.

Jednostka ładunku elektrycznego - kulomb, została nazwana również od nazwiska Charles'a Coulomba), jest ona równa połączonym ładunkom 6,24 x 10¹⁸ protonów (lub elektronów).

Strumień pola jest wielkością skalarną opisującą pole wektorowe oraz jego źródłowość. Definicja formalna strumienia pola opisywanego wektorem
przechodzącego przez daną powierzchnię S to:

Definicja ta jest zgodna z intuicyjnym pojęciem strumienia, np. jeżeli jako pole wektorowe weźmiemy iloczyn gęstości wody i jej prędkości w danym punkcie (pole prędkości) to strumień takiego pola będzie opisywał ilość(masę) wody przechodzącą przez zadaną powierzchnię w jednostce czasu, czyli to co intuicyjnie rozumiemy jako strumień.

Szczególnie ważnym pojęciem jest strumień przechodzący przez powierzchnię zamkniętą:

Jeżeli wartość tego strumienia jest większa od zera oznacza to, że pole jest źródłowe i posiada wewnątrz tej powierzchni "źródło" (np. dla pola elektrycznego ładunek dodatni, dla analogii z wodą rurę wpływową), jeżeli wartość ta jest ujemna pole posiada "odpływ" (ładunek ujemny, rurę odpływową).

W różniczkowym ujęciu źródłowości odpowiada operator dywergencji.

23. Energia w ruchu harmonicznym.

19. Oscylator harmoniczny (definicja , model)

Oscylator harmoniczny w naukach ścisłych to model teoretyczny opisujący układ w parabolicznym potencjale — potencjał oscylatora harmonicznego, bądź krócej potencjał harmoniczny, czyli kwadratowa zależność potencjału od odległości
, gdzie r jest odległością w N-wymiarowej przestrzeni, N zależy od konkretnej realizacji modelu. Ze względu na skalę modelowanych zjawisk wyróżnia się klasyczny oscylator harmoniczny oraz kwantowy oscylator harmoniczny.

Z matematycznego punktu widzenia potencjał paraboliczny jest najprostszym potencjałem lokalizującym, który warto rozważać teoretycznie. Prostsze potencjały nie są interesujące, gdyż:

• potencjał stały to cząstka swobodna

• liniowa zależność

• w mechanice klasycznej oznacza stałą siłę

• w mechanice kwantowej potencjał liniowy wymaga doprecyzowania, gdyż bez określenia warunków brzegowych problem jest źle postawiony (odpowiednie rozwiązanie równania Schrödingera bez warunków brzegowych ma nieograniczone z dołu widmo).

Innym powodem, dla którego model oscylatora harmonicznego jest tak często eksploatowany w naukach ścisłych wynika z tego, że istnieje bardzo wiele funkcji potencjału, które można przybliżyć wokół minimum zależnością kwadratową. Matematycznym warunkiem byłaby istniejąca i nieznikająca druga pochodna funkcji potencjału w minimum. W praktyce oznacza to, że wiele zagadnień świata realnego daje się sprowadzić do zagadnienia oscylatora harmonicznego. Przykładami takich zagadnień są:

• mechanika klasyczna

• wahadło matematyczne

• wahadło fizyczne

• masa na sprężynie

• małe drgania harmoniczne

• mechanika kwantowa

• drgania sieci krystalicznej

• potencjał jądrowy

• kropka kwantowa

Zagadnienie oscylatora harmonicznego jest ściśle rozwiązywalne zarówno w mechanice klasycznej (klasyczny oscylator harmoniczny) jak i mechanice kwantowej (kwantowy oscylator harmoniczny).

Drgania inne niż harmoniczne (tzn. dla potencjałów opisywanych innymi zależnościami niż kwadratowymi, bądź nie dające się sprowadzić do potencjału harmonicznego) określa się drganiami anharmonicznymi. Poprawki do ruchu harmonicznego wynikające z innych zależności potencjału niż kwadratowa nazywa się poprawkami anharmonicznymi.

Nazewnictwo

W związku z tym, że oscylator harmoniczny jest obecny we wszystkich dziedzinach fizyki, to bardzo często przez oscylator harmoniczny rozumie konkretną realizację modelu. Nazwa ta jest używana wszędzie tam, gdzie nie budzi ona wątpliwości, a wyjaśnieniem jest kontekst, w jakim się pojawia.

Przykłady oscylatorów.

Wahadło - ciało zawieszone lub zamocowane ponad swoim środkiem ciężkości wykonujące w pionowej płaszczyźnie drgania pod wpływem siły grawitacji. W teorii mechaniki rozróżnia się dwa podstawowe rodzaje wahadeł:

• matematyczne

• fizyczne


Wahadło matematyczne [edytuj]

Punkt materialny zawieszony na nierozciągliwej i nieważkiej nici. Jest to idealizacja wahadła fizycznego.

Ważną cechą wahadła fizycznego i matematycznego jest stałość okresu drgań dla niewielkich wychyleń wahadła.

Wahania swobodne [edytuj]

W wahadle matematycznym poruszające się ciało jest masą punktową, zawieszoną na nieważkiej nitce o długości l. Na ciało to działa stała siła grawitacji. Gdy wahadło odchylone jest z położenia równowagi składowa siły grawitacji wzdłuż nici jest równoważona przez nić, a składowa prostopadła do nici działająca w kierunku punktu równowagi nadaje ciału przyspieszenie. Ruch ciała ograniczony nicią, jest ruchem po okręgu. Na podstawie definicji przyspieszenia kątowego, oraz II zasady dynamiki dla ruchu punktu materialnego po okręgu wynika:







Dla kątów wyrażonych w radianach, które w tych jednostkach są znacznie mniejsze od 1, funkcję sinus można przybliżyć jej argumentem, co prowadzi do równania:




Powyższe równanie jest równaniem ruchu drgającego harmonicznego, którego ogólna postać jest dana wzorem:




gdzie
jest częstością kołową drgań a T - okresem. Wynika stąd, że okres drgań wynosi




Takie drgania wahadła matematycznego (bez działania sił zewnętrznych) nazywamy drganiami własnymi wahadła.

Ogólny przypadek drgań tłumionych i wymuszonych wahadła matematycznego [edytuj]

Ogólne równanie ruchu wahadła matematycznego:




Gdzie:

• l - długość nici,

• g - przyspieszenie ziemskie,

• m - masa ciała,

• θ - kąt wektora wodzącego ciała z pionem

• A - amplituda siły wymuszającej

• ω_D - częstość siły wymuszającej

• γ - współczynnik oporu ośrodka

Równanie to odpowiada równaniu drgań tłumionych o sile nieproporcjonalnej do wychylenia, czyli drgań nieharmonicznych. Równania tego nie da się rozwiązać analitycznie, nawet gdy A=0.

Dla małych wychyleń funkcję sinus można przybliżyć przez zastosowanie prawidłowości:




Stosując powyższe przybliżenie, pomijając opory oraz siłę wymuszającą, równanie otrzymuje postać:




Równanie, to odpowiada równaniu oscylatora harmonicznego o częstości:







Zależność okresu drgań wahadła T od kąta wychylenia θ.

Z rozwiązania przybliżonego ruchu wahadła wynika, że dla małych kątów wychylenia okres drgań wahadła jest niezależny od masy wahadła, amplitudy drgań wahadła, a zależy tylko od długości i przyspieszenia ziemskiego. Warunki przybliżenia są w miarę dobrze spełnione dla wychyleń mniejszych niż 8 stopni.

Gdy nie występuje wymuszanie drgań ani opór ośrodka, okres drgań może być wyrażony wzorem:




gdzie E(k,φ) jest funkcją eliptyczną Legendre'a pierwszego rodzaju:


.

Okres drgań można również przedstawić jako sumę nieskończonego szeregu:




W tej postaci widać wyraźnie różnicę pomiędzy przybliżonym i dokładnym rozwiązaniem równania ruchu wahadła.

W ogólności ruch wahadła rozpatruje się jako drgania, odpowiednio swobodne, tłumione, wymuszone.

Wahadło fizyczne [edytuj]

Bryła sztywna mogąca wykonywać obroty dookoła poziomej osi przechodzącej ponad środkiem ciężkości tej bryły.

Wzór na okres drgań wahadła fizycznego dla małych wychyleń:




Przez analogię do wahadła matematycznego wzór ten zapisuje się jako:


,

wprowadzając wielkość długość zredukowana wahadła l₀




gdzie:

• d - odległość od punktu zawieszenia do środka ciężkości,

• g - przyspieszenie ziemskie,

• I - moment bezwładności ciała względem osi obrotu,

• m - masa ciała

20. Ogólne równanie oscylatora harmonicznego - wyprowadzenie z zasad dynamiki




Definicja oscylatora harmonicznego

Ścisła definicja jednowymiarowego oscylatora harmonicznego mówi, że jest to każdy układ fizyczny, którego zachowanie można opisać równaniem, zwanym równaniem oscylatora harmonicznego:


,

gdzie:

• a(t) - przyspieszenie zależne od czasu,

• x(t) - położeniem zależne od czasu,

• ω₀ - częstośc drgań oscylatora harmonicznego.

Związek ten można zapisać jawnie jako liniowe równanie różniczkowe




lub korzystając z konwencji stosowanej w mechanice, gdzie pochodną po czasie oznacza się kropką




Model opisywany powyższym równaniem nazywa się też czasem prostym oscylatorem harmonicznym. Każdy układ, którego równanie można sprowadzić do powyższego określa się w skrócie jako oscylator harmoniczny.

Rozwiązanie równania oscylatora [edytuj]

Rozwiązanie równania oscylatora harmonicznego można zapisać w jednej z poniższych równoważnych postaci

1. 
   

2. 
   

3. 
   

4. 
   

gdzie
stałe zależne od warunków początkowych. Rozwiązania są równoznaczne, a korzystając z tożsamości trygonometrycznych można znaleźć zależności pomiędzy powyższymi stałymi i rozwiązanie przedstawiać w dowolnej z postaci 1,2,3.

ω₀ jest częstością kołową oscylatora harmonicznego. Okres drgań T wynosi




częstotliwość drgań ν natomiast wynosi




21. Wielkości charakterystyczne występujące w rozwiązaniu oscylatora harmonicznego związki między nimi: amplituda, częstość, częstotliwość, okres drgań, faza, faza początkowa



Oscylator harmoniczny to układ, na który, przy wytrąceniu ze stanu równowagi, działa siła proporcjonalna do wychylenia, usiłująca tą równowagę przywrócić. Skutkiem tego jest ruch ograniczony w przestrzeni i drgający harmonicznie, czyli taki, w którym zależność odchylenia od czasu ma postać funkcji sinus lub cosinus.

Prostym przykładem mechanicznego oscylatora harmonicznego jest ciężarek o masie m zawieszony na sprężynie. Prawo Hooke'a mówi, że na ciało na odkształcanej sprężynie działa siła skierowana przeciwnie do kierunku odkształcenia i proporcjonalna do odległości od stanu równowagi (sprężyny nieodkształcanej). Możemy to zapisać:

F_p = - kx

x - odległość od punktu równowagi, F_p - siła sprężystości, k - współczynnik sprężystości

Równanie ruchu dla masy zawieszonej na sprężynie jest proste, gdy pominiemy siłę grawitacji lub umieścimy układ w stanie nieważkości.
Działa wtedy na nią jedynie „przywracająca” siła sprężystości (sprężyna stawia opór ściskaniu i rozciąganiu).
A więc, równanie ruchu masy m możemy, zgodnie z drugim prawem dynamiki Newtona, zapisać następująco:

ma = F_p

Wiemy, że przyspieszenie (a) to druga pochodna położenia po czasie; zatem otrzymujemy:

m(d²x/dt²) = -kx

Jest to proste równanie różniczkowe, którego rozwiązaniem jest taka funkcja x(t), która pokazuje jak położenie tej masy zależy od czasu.
Równanie to należy czytać następująco: jaka funkcja ma taką właściwość, że jej druga pochodna pomnożona przez m daje ją samą pomnożoną przez -k?
Okazuje się, że taką własność ma funkcja: x = A sin(ω_ot + φ), gdzie:




Teraz parę słów objaśnień użytych symboli:

• A - amplituda przedstawiająca maksymalne wychylenie x_max. Jest tak dlatego, że maksymalną wartością funkcji sinus jest 1, czyli x_max = A razy 1 = A.

• ω_o - częstość własna drgań oscylatora - określa liczbę pełnych drgnięć w jednostce czasu. Jak widać z powyższego wzoru na ω_o, spada ona ze wzrostem masy m i rośnie ze wzrostem współczynnika k, będącego miarą sprężystości sprężyny.

• φ - faza początkowa drgań - określa stan w jakim znajdował się oscylator na początku drgań (t=0). Na przykład gdy φ = 0, to x = A sin ω_ot i dla t=0 wychylenie x=0, czyli oscylator rozpoczął drgania od stanu równowagi.
  Inny przykład: φ = 2π → x = A sin(ω_ot + 2π) = A cos ω_ot , zatem dla t=0 wychylenie x=A, czyli oscylator rozpoczyna drgania od stanu maksymalnego wychylenia.

Rzeczywisty oscylator harmoniczny jest tłumiony, bo np. sprężyna nie drga w nieskończoność, tylko po pewnym czasie wytraca swoją energię w postaci ciepła (wskutek tarcia). A więc, w rzeczywistości będziemy obserwować ruch oscylacyjny złożony z zanikiem wykładniczym, czyli po prostu drgania o coraz mniejszej amplitudzie. Przy bardzo silnym tłumieniu nie wystąpi ani jedno drgnięcie, ale od razu wykładniczy zanik ruchu.

Jeśli na oscylator działa dodatkowo zewnętrzna siła (również o oscylującej wartości), to mamy do czynienia z jego drganiami wymuszonymi. Mają one taką częstotliwość jak siła wymuszająca F_o cos ωt.

Oto równanie ruchu:

m(d²x/dt²) = - kx + F_o cos ωt

Amplituda oscylacji obliczana jest wtedy według wzoru:

A = F_o / [m(ω_o² - ω²)]

gdzie: ω_o - własna częstotliwość drgań oscylatora, ω - częstotliwość drgań siły wymuszającej.

Widzimy, że amplituda przybiera bardzo duże wartości dla ω bardzo zbliżonego wartością do ω_o (mały mianownik). Jeśli jednak ω = ω_o, to mamy do czynienia z osobliwością. Równanie „wybucha”, bo mamy zero w mianowniku, co sugeruje nieskończoną amplitudę.
Oczywiście, w rzeczywistym świecie nigdy z czymś tak nierealnym nie mamy do czynienia. Jest tak dlatego, że każdy realny oscylator jest tłumiony, co objawia się tym, że nawet gdy siła wymuszająca drga zgodnie z częstością własną oscylatora (ω = ω_o), to mianownik nie jest zerem, bo pojawia się tam człon związany ze współczynnikiem tarcia.
Jednak amplituda osiąga wtedy największą, aczkolwiek skończoną wartość. Zjawisko, z którym mamy wtedy do czynienia to tzw. rezonans.

22. Prędkość i przyspieszenie w ruchu harmonicznym

Ponieważ przyspieszenie ma przeciwny zwrot do wychylenia to we wzorze na przyspieszenie pojawia się znak minus. a=-Asint, a=-x

ω=2π/T, x=rsinα, x(t)=Asinωt - położenie punktu

υ=1/T - częstotliwość

V=ωAcosωt V=2πr/T=ωr - prędkość

a₁=a_dsinα - przyspieszenie

a_d=ωr=V²/r - przysp punktu poruszającego się po okręgu

a=-ω²x=-ω²Asinωt - przyspieszenie

T=2π√(m/k) - okres drgań, ω=√k/m - częstość

ω=2πυ υ- częstotliwość

T=2π√(m/k) - okres drgań, ω=√k/m - częstość

F1/Fg=sinα, F1=mgsinα, x/l=tgα

F=-mg(x/l)= -mg/l*x

ω=√g/l - częstość, T=2π √l/g - okres drgań

Ruch drgający można rozpatrywać jako rzut ruchu po okręgu.




Z rysunku odczytujemy, że:






Przekształcając równania otrzymujemy równanie ruchu drgającego.

Ruch drgający, odbywający się pod działaniem siły sprężystości, w którym przyspieszenie w każdym punkcie ruchu jest wprost proporcjonalne do wychylenia, nosi nazwę ruchu drgającego prostego albo harmonicznego.Ciało drgające to oscylator harmoniczny.



Jak widać w równaniu ruchu drgającego wychylenie w ruchu harmonicznym zmienia się w czasie sinusoidalnie. Tą zależność przedstawia wykres:




Prędkość, przyspieszenie i siła


Rozważmy ponownie ruch harmoniczny jako rzut ruchu jednostajnego po okręgu. Wykorzystując zależności pokazane na rysunku wyprowadźmy wzór na prędkość w ruchu harmonicznym.




prędkość ciała poruszającego się po okręgu

składowa prędkości


promień okręgu




Korzystamy z wzoru na prędkość w ruchu po okręgu:




Jak wynika z rysunku za r możemy podstawić A (największe wychylenie) i otrzymuje wzór na prędkość w ruchu harmonicznym.






Prędkość maksymalną ciała osiąga w położeniu równowagi.

Zależność prędkości od czasu w ruchu harmonicznym przedstawia wykres:




Wzór na prędkość w ruchu harmonicznym można także wyprowadzić obliczając pochodną V=dx/dt.

Wykonajmy podobny rysunek i wyprowadźmy wzór na przyspieszenie w ruchu harmonicznym.




Korzystając z rysunku odczytujemy zależności:




Za
podstawiamy wzór na przyspieszenie w ruchu po okręgu:




Otrzymujemy wzór na przyspieszenie w ruchu harmonicznym:




Znak minus oznacza, że kierunek przyspieszenia jest przeciwny względem kierunku wychylenia.
Przyspieszenie maksymalne ciało osiąga w punkcie największego wychylenia:




Zależność przyspieszenia od czasu w ruchu harmonicznym przedstawia wykres:




Wzór na przyspieszenie w ruchu harmonicznym można wyprowadzić także obliczając pochodną a=dV/dt.

Ruch drgający prosty jest ruchem niejednostajnie zmiennym.

23. Energia w ruchu harmonicznym

Przemiany energii


Ciało drgające posiada energię kinetyczną i potencjalną sprężystości. Wyprowadźmy wzory na obie energie.
Energia potencjalna sprężystości wyraża się ogólnym wzorem:




Po podstawieniu do tego wzoru równanie ruchu drgającego otrzymujemy wzór na energię potencjalną sprężystości w ruchu drgającym:




Energia kinetyczna wyraża się ogólnym wzorem:




Wstawiamy do niego wzór na prędkość prędkość ruchu harmonicznym i otrzymujemy wzór na energię kinetyczną w ruchu drgającym:




A więc energia całkowita ciała drgającego wynosi:




Energia całkowita jest proporcjonalna do kwadratu amplitudy.




36

---