1. Wyznaczenie koncentracji nośników n.

Napięcie Halla Uh	Prąd Sterujący Is	Prąd elektromagnesu	Indukcja B	dUh	dIs
[mV]	[ mA]	[A]	[ mT ]	[mV]	[mA]
0	0	0	0	0	0
24,6	3,08	0,5	6	0,13	0,016
28,7	3,59	0,5	6	0,15	0,019
34,6	4,33	0,5	6	0,18	0,023
50,0	6,29	0,5	6	0,26	0,032
71,5	9,01	0,5	6	0,37	0,046
93,5	11,83	0,5	6	0,48	0,060

Błąd natężenia sterującego jak i napięcia Halla określamy korzystając z danych miernika elektronicznego tzn. ± 0,5% pomiaru + 1 do ostatniej cyfry.

Poniżej przedstawiamy wykres zależności napięcia Halla od natężenia sterującego i spadku napięcia na hallotronie od natężenia sterującego.

Prosta otrzymana na wykresie ma postać funkcji liniowej, co wskazuje na proporcjonalność napięcia Halla do natężenia sterującego.

Te zależności wykorzystamy bezpośrednio do obliczenia koncentracji .

IE	IE = 0,5 A	Odchylenie
Uh	50,5	0,26
Is	6,36	0,033

Dane hallotronu:

d = 100 ± 1 μm

c = 2,5 ± 1 mm

l = 10,0 ± 0,1 mm

Dla I_E = 0,5 A, B=0,06 T:

dB=0,01 T

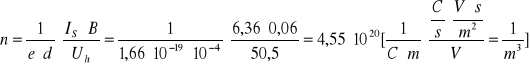
odchylenie:

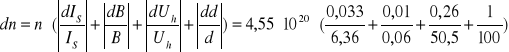
n = (4,55 ± 0,085)∙10²⁰

Przeprowadzone doświadczenie potwierdza liniowa zależność między napięciem Halla (i spadkiem napięcia na hallotronie) a natężeniem sterującym. Ta proporcjonalność pozwoliła nam na obliczenie koncentracji nośników n.

2.Wyznaczenie koncentracji nośników n1 i ich ruchliwości µ.

Prąd elektromagnesu Ie	Indukcja B	Napięcie Halla Uh	Napięcie elektromagnesu Ue	Prąd Sterujący Is	dUh	dIs
[A]	[T]	[mV]	[V]	[A]	[mV]	[A]
0	0	0	0	0	0	0
0,178	0,030	30,4	2,01	10,00	0,16	0,06
0,210	0,034	34,9	2,01	10,00	0,18	0,06
0,281	0,038	44,7	2,01	10,00	0,23	0,06
0,358	0,045	55,4	2,01	10,00	0,29	0,06
0,410	0,058	69,9	2,01	10,00	0,36	0,06
0,508	0,062	76,3	2,01	10,00	0,39	0,06
0,579	0,071	85,7	2,01	10,00	0,44	0,06
0,672	0,083	99,3	2,01	10,00	0,51	0,06
0,746	0,092	109,7	2,02	10,00	0,56	0,06
0,781	0,096	114,5	2,02	10,00	0,58	0,06
0,834	0,100	122,0	2,02	10,00	0,62	0,06
0,900	0,110	131,2	2,02	10,00	0,67	0,06
0,985	0,118	143,1	2,02	10,00	0,73	0,06
1,052	0,121	152,5	2,02	10,00	0,77	0,06
1,112	0,130	161,1	2,03	10,00	0,82	0,06
1,234	0,147	178,0	2,03	10,00	0,90	0,06

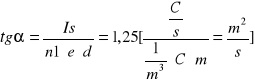
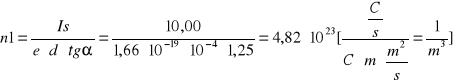
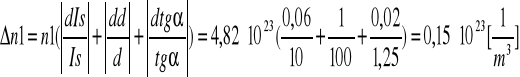
Ue=2,02[V]

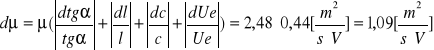
3. Wyznaczenie magnetooporu .

Ue	Is	dUe	dIs	R=Ue/Is	dR	B
[V]	[A]	[V]	[A]	[Ω]	[Ω]	[T]
2,01	10,00	0,02	0,06	0,2010	0,003	0,0300
2,01	10,00	0,02	0,06	0,2010	0,003	0,0350
2,01	10,00	0,02	0,06	0,2010	0,003	0,0380
2,01	10,00	0,02	0,06	0,2010	0,003	0,0450
2,01	10,00	0,02	0,06	0,2010	0,003	0,0580
2,01	10,00	0,02	0,06	0,2010	0,003	0,0620
2,01	10,00	0,02	0,06	0,2010	0,003	0,0710
2,01	10,00	0,02	0,06	0,2010	0,003	0,0830
2,02	10,00	0,02	0,06	0,2020	0,003	0,0920
2,02	10,00	0,02	0,06	0,2020	0,003	0,0960
2,02	10,00	0,02	0,06	0,2020	0,003	0,1000
2,02	10,00	0,02	0,06	0,2020	0,003	0,1100
2,02	10,00	0,02	0,06	0,2020	0,003	0,1180
2,02	10,00	0,02	0,06	0,2020	0,003	0,1210
2,03	10,00	0,02	0,06	0,2030	0,003	0,1300
2,03	10,00	0,02	0,06	0,2030	0,003	0,1470

Współczynnik kierunkowy prostej wynosi: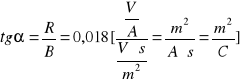

Wnioski.

W doświadczeniu wykazaliśmy liniową zależność napięcia Halla (Uh) od prądu sterującego (Is) i indukcji magnetycznej (B). Powyższe zależności przedstawione są na wykresach. Pozwoliły one na wyznaczenie koncentracji i ruchliwości nośników.

Koncentrację n wyznaczyliśmy na podstawie wzoru
. Przy przyjętych wartościach I_E = 0,5 A, B=0,06 T i średnich wartościach Uh=50,5±0,26V i Is=6,36±0,033A otrzymaliśmy wynik n = (4,55 ± 0,085)∙10²⁰
Wykres I.

Koncentrację (n1) wyznaczyliśmy dla 16 różnych wartości napięcia hallotronu i wartości indukcji (B) i przy stałej wartości Is=10A . Na podstawie wykresu otrzymaliśmy współczynnik kierunkowy naszej prostej, który użyliśmy do naszych obliczeń.

.Wykres II.

Ruchliwość wyznaczyliśmy ze wzoru

. W tym przypadku również skorzystaliśmy ze współczynnika kierunkowego prostej i średniej wartości Ue=2,02V.

Na koniec wyznaczyliśmy związek pomiędzy oporem elektromagnesu, a polem elektromagnetycznym (B), tak zwany magnetoopór, co zostało przedstawione na ostatnim wykresie.

---