Elementarne skale długości

Kwadrat elementarnej skali zniekształceń długości ma postać

gdzie

Wyznaczamy pochodną:

przyrównujemy do zera i podstawiamy za A, A_e:

Stąd wyznaczamy kierunek ekstremalnych zniekształceń:

Mając dany kierunek ekstremalnych zniekształceń możemy wyznaczyć ekstremalne skale długości:

Mając dane skale ekstremalne wzór na skalę w dowolnym kierunku można zapisać w postaci:

gdzie

I i II twierdzenie Apoloniusza

Skale
są półśrednicami sprzężonymi w elipsie zniekształceń ponieważ spełniają dwa twierdzenia Apoloniusza:

I twierdzenie Apoloniusza

sumując stronami i porządkując mamy:

II twierdzenie Apoloniusza

pole równoległoboku, zbudowanego na półśrednicach sprzężonych elips, jest równe polu prostokąta, zbudowanego na osiach elipsy.

Sprawdzenie:

Mamy dane wzory:

Obliczamy moduł iloczynu wektorowego:

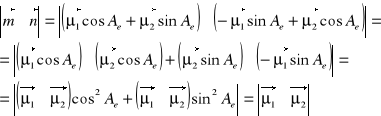
Zależności pomiędzy skalami ekstremalnymi a półśrednicami sprzężonymi elipsy zniekształceń odwzorowawczych

Z I twierdzenia Appoloniusza mamy

Z II twierdzenia Appoloniusza mamy
Podnosząc do kwadratu sumę i różnicę skal ekstremalnych, oraz uwzględniając powyższe rozważania otrzymujemy:

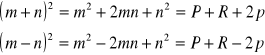
Stąd wyznaczamy sumę i różnicę skal ekstremalnych:

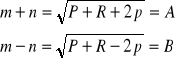
dodając lub odejmując stronami powyższe równania otrzymujemy:

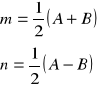
Elementarne skale zniekształcenia pól

Elementarne pole na powierzchni opisanej równaniem
można przedstawić następująco:

Elementarna skala zniekształceń pól jest to stosunek odpowiadających sobie elementarnych pól na powierzchni obrazu i na powierzchni oryginału

gdzie dP - elementarne pole na powierzchni oryginału,

dP' - elementarne pole na powierzchni obrazu.

Podstawiając wzory na elementarne łuki otrzymujemy:

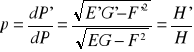
Jeżeli w danym odwzorowaniu kartograficznym wyznaczymy elementarne skale zniekształceń długości m, n w kierunkach głównych wówczas p = Mn

Zniekształcenia kątów

Zniekształceniem dowolnego kąta A nazywamy różnicę pomiędzy odpowiadającymi sobie kątami na powierzchni obrazu i powierzchni oryginału

A - kąt pomiędzy krzywymi na powierzchni oryginału

A' - kąt pomiędzy obrazami tych krzywych na powierzchni obrazu

Zależności pomiędzy kątem kierunkowym A na powierzchni oryginału a jego obrazem A' w odwzorowaniu kartograficznym

Tangens kąta kierunkowego A' można obliczyć na podstawie kąta A ze wzoru:

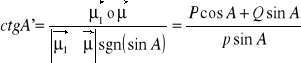
Stąd ostatecznie mamy:

Zależność pomiędzy kątem kierunkowym β = A - A_e a jego obrazem β'

Tangens kąta kierunkowego β' można obliczyć ze wzoru:

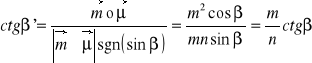
Stąd ostatecznie mamy:

Ekstremalne zniekształcenia dowolnego kąta γ

Dowolny kąt γ możemy zdefiniować jako różnicę dwóch kierunków β₁ oraz β₂

Kąt γ' będący obrazem kąta γ można zapisać w postaci

Zniekształcenie kąta γ z definicji

W związku z tym można napisać, że

Na podstawie powyższego wzoru można oszacować

Ekstremalne zniekształcenia kąta kierunkowego β = A - A_e

Zniekształcenie kierunku β jest z definicji równe

Wyznaczamy

uwzględniając

otrzymujemy

Ekstremalne zniekształcenie dowolnego kąta γ

Funkcja powyższa osiąga ekstremum wówczas, gdy mianownik osiąga ekstremum, wyznaczamy więc ekstremum następującej funkcji

W tym celu liczymy pochodną

i przyrównujemy do zera podstawiając za β, β_m

Stąd otrzymujemy kierunek najbardziej ulegający zniekształceniu

Ostatecznie wzór na ekstremalne zniekształcenie kąta kierunkowego β ma postać

Ponieważ
stąd zniekształcenie dowolnego kąta γ zawiera się w przedziale

Kąt między liniami parametrycznymi na powierzchni oryginału i na powierzchni obrazu w odwzorowaniu kartograficznym

Równanie parametryczne powierzchni oryginału ma postać

Kąt θ pomiędzy liniami parametrycznymi można wyznaczyć w następujący sposób:

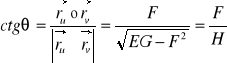
Równanie parametryczne powierzchni obrazu ma postać:

Kąt θ' pomiędzy liniami parametrycznymi można wyznaczyć w następujący sposób:

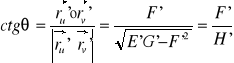
Zbieżność południków w odwzorowaniach kartograficznych

W odwzorowaniu kartograficznym określonym równaniem

zbieżność południków można określić za pomocą wzoru

---