Rodzaje konstrukcji z betonu
Różnica w koncepcji konstrukcji żelbetowych i sprężonych
Rodzaje konstrukcji sprężonych wz. od technologii sprężenia
Rola łączników w konstrukcjach zespolonych
wyjaśnij dlaczego w konstrukcjach sprężonych jest lepsze wykorzystanie właściwości mechanicznych stali niż w konstrukcjach żelbetowych (a może jest inaczej?)
Dlaczego panuje pogląd, że zbrojenie w konstrukcjach żelbetowych pełni pasywną rolę?
Właściwości mechaniczne betonu
Czy wytrzymałość betonu na ściskanie określoną na kostkach 150x150x150mm można uznać za wytrzymałość w jednoosiowym stanie naprężenia. Odpowiedź uzasadnij
W jaki sposób określa się wytrzymałość betonu:
na ściskanie w jednoosiowym stanie naprężenia
na rozciąganie
Wpływ stosunku wysokości do wymiaru przekroju poprzecznego próbki na wytrzymałość betonu na ściskanie
Próbki stosowane do określania wytrzymałości betonu na ściskanie. Czy rodzaj zastosowanej próbki ma wpływ na wartość tej wytrzymałości? Od czego zależy najmniejszy wymiar kostki?
Czy wytrzymałość betonu na rozciąganie jest proporcjonalna do jego wytrzymałości na rozciąganie. Przedstaw poglądowy wykres tej zależności
Przedstaw szkic zależności wytrzymałości betonu w dwuosiowym stanie naprężenia od stosunku naprężeń w obu kierunkach
Wpływ stosowania szczotek Hilsdorfa na wytrzymałość betonu na ściskanie
Prędkość przyrostu obciążenia a wytrzymałość betonu na ściskanie
Wykres odkształcalności podłużnej betonu
Współczynnik Poissona dla betonu
Odkształcalność podłużna betonu dla różnych klas
Rodzaje modułów sprężystości betonu.
Średni moduł sprężystości betonu
Odkształcalność termiczna betonu
Co to jest wytrzymałość charakterystyczna betonu. Przy jakim poziomie ufności jest ona określana.
Omówić pojęcie wytrzymałości średniej, charakterystycznej i obliczeniowej betonu na ściskanie i rozciąganie.
Mając zbadane n>30 próbek kostkowych 150x150x150mm określ procedurę wyznaczania wytrzymałości charakterystycznej betonu na ściskanie.
Skurcz betonu. Przebieg skurczu w czasie
Omówić zjawisko pełzania i relaksacji.
Kiedy mamy do czynienia z pełzaniem liniowym a kiedy z nieliniowym?
Konsekwencje skurczu betonu w konstrukcjach żelbetowych i sprężonych
Modelowanie skurczu betonu w obliczeniach statycznych. Podstawa tego modelowania
Pełzanie betonu i czynniki je determinujące
Przebieg odkształceń od skurczu i pełzania betonu w czasie, podczas obciążenia i odciążenia
Przedstawić redystrybucję naprężeń w betonie i stali zachodzącą wskutek pełzania w:
pojedynczo zbrojonym zginanym przekroju żelbetowym
osiowo ściskanym przekroju żelbetowym
osiowo ściskanym przekroju betonowym
Czynniki wpływające na skurcz betonu
Czynniki wpływające na pełzanie betonu
Mając podane wiek betonu w chwili obciążenia, rodzaj użytego cementu, klasę wytrzymałości betonu i miarodajny wymiar elementu określ za pomocą podanego nomogramu końcowy współczynnik pełzania
Wpływ pełzania na moduł sprężystości betonu
opisz metodę wyznaczania średniego siecznego modułu sprężystości betonu
Właściwości mechaniczne stali
Parametry charakteryzujące ciągliwość stali (pokaż na wykresie). Podział stali ze względu na ciągliwość
Co to jest umowna granica plastyczności stali (pokaż na wykresie)?
Jaka jest rola otulenia zbrojenia w konstrukcjach żelbetowych? Omówić czynniki wpływające na grubość otulenia.
Od czego zależy graniczne naprężenie przyczepności?
Co to jest długość zakotwienia?
Czynniki wpływające na długość zakotwienia
Zasady kotwienia strzemion
Zasady łączenia prętów na zakład
Zginanie
Omówić fazy wytężenia zginanego przekroju żelbetowego
Sposób wyznaczenia wysokości strefy ściskanej w fazie Ia i IIa. Napisać odpowiednie równania, z których te wysokości się wylicza
Podać ogólny wzór, dla dowolnego przekroju na moment rysujący
Co to jest przekrój minimalny i w jakim celu się go wprowadza?
Omówić pojęcie granicznej wysokości względnej przekroju zginanego
Co to jest graniczny przekrój zbrojenia. Wyprowadzić wzór na graniczny stopień zbrojenia
Mechanizmy zniszczenia zginanego przekroju żelbetowego. Związek między stopniem zbrojenia a mechanizmem zniszczenia zginanego przekroju żelbetowego
Co to jest przekrój podwójnie zbrojony. Kiedy stosuje się taki przekrój i jakie warunki muszą zostać spełnione?
Co to jest przekrój przezbrojony. Czy przekrój podwójnie zbrojony może być przezbrojony?
Kiedy przekrój teowy uważa się za pozornie teowy?
Przedstawić procedurę wymiarowania zginanego prostokątnego przekroju żelbetowego, pojedynczo i podwójnie zbrojonego
Przedstawić procedurę wymiarowania zginanego teowego przekroju żelbetowego, pojedynczo i podwójnie zbrojonego
Przedstawić procedurę wyznaczania nośności pojedynczo zbrojonego zginanego przekroju prostokątnego
Przedstawić procedurę wyznaczania nośności podwójnie zbrojonego zginanego przekroju prostokątnego
Przedstawić procedurę wyznaczania nośności podwójnie zbrojonego zginanego przekroju teowego
Przedstawić procedurę wyznaczania nośności pojedynczo zbrojonego zginanego przekroju teowego
Przedstawić procedurę wyznaczania nośności podwójnie zbrojonego, przezbrojonego zginanego przekroju teowego
Jak wyznacza się nośność zginanego podwójnie zbrojonego przekroju żelbetowego przy bardzo małej wysokości obliczeniowej strefy ściskanej (xeff nie przekracza 2a2). Uzasadnić taki sposób obliczania.
Wykorzystanie nośności belki żelbetowej do kształtowania zbrojenia na zginanie
Zasady kształtowania zbrojenia głównego i drugorzędnego w płytach ciągłych (omówić także maksymalne i minimalne rozstawy prętów)
Ściskanie ze zginaniem
Co to jest smukłość. Kiedy należy uwzględniać wpływ smukłości. Co to jest smukłość graniczna?
Naszkicuj związek między nośnością elementu ściskanego a smukłością dla różnych mimośrodów siły
Naszkicuj związek między nośnością słupa żelbetowego a mimośrodem siły
Co to jest wykres interakcyjny i jak się go tworzy. Co reprezentuje punkt znajdujący się:
wewnątrz wykresu interakcyjnego
na krzywej nośności granicznej
na zewnątrz wykresu interakcyjnego
Mechanizmy zniszczenia mimośrodowo ściskanego słupa żelbetowego na tle wykresu interakcyjnego.
Możliwe stany odkształcenia zginanego i ściskanego przekroju żelbetowego w stanie granicznym nośności.
Kryterium zniszczenia mimośrodowo ściskanego przekroju żelbetowego. Czy wartość granicznego skrócenia betonu jest stała?
Zasady określania mimośrodu konstrukcyjnego w słupach o węzłach przesuwnych i nieprzesuwnych.
Sposoby uwzględniania imperfekcji geometrycznych podczas wymiarowania słupa.
Metody wyznaczania efektów II rzędu.
Jak się wyznacza maksymalną krzywiznę przy obliczaniu efektów II rzędu metodą nominalnej krzywizny.
Jakie są założenia (uproszczenia) metody nominalnej krzywizny.
Przedstaw procedurę wymiarowania smukłego słupa żelbetowego o znanej długości obliczeniowej.
Podaj procedurę wymiarowania mimośrodowo ściskanego przekroju żelbetowego w przypadku dużego mimośrodu (przy znanym etot)
Wymiarowanie symetrycznie zbrojonego mimośrodowo ściskanego przekroju żelbetowego. Kiedy można stosować tę procedurę.
Po czym rozpoznaje się przypadek małego mimośrodu.
Dlaczego procedura wymiarowania symetrycznie zbrojonego mimośrodowo ściskanego przekroju żelbetowego, stosowana w przypadku tzw. dużego mimośrodu może/nie może być stosowana w przypadku tzw. małego mimośrodu
Przedstaw model obliczeniowy do wymiarowania mimośrodowo ściskanego przekroju żelbetowego w przypadku gdy wysokość strefy ściskanej nie przekracza 2a2. Wyjaśnij dlaczego stosuje się ten model i podaj wzór na wyznaczenie AS1.
Zasady zbrojenia słupów żelbetowych
Rola strzemion w słupach żelbetowych.
Kryterium podziału słupów na krępe i smukłe.
Wpływ przebiegu momentów zginających na długości słupa na jego długość obliczeniową
Wpływ pełzania na efekty II rzędu
Wpływ wielkości mimośrodu początkowego na efekty II rzędu
Kiedy w słupach ram można pomijać efekty II rzędu?
Przykładowe pytania testowe
Długość zakotwienia, przy tym samym przekroju zbrojenia:
wzrasta wraz ze wzrostem średnicy zastosowanych prętów,
maleje wraz ze wzrostem średnicy zastosowanych prętów,
jest niezależna od średnicy zastosowanych prętów,
w strefie rozciąganej wzrasta wraz ze wzrostem średnicy zastosowanych prętów, natomiast w strefie ściskanej maleje wraz ze wzrostem średnicy zastosowanych prętów.
Przekrój pozornie teowy to przekrój o kształcie teowym, w którym:
półka znajduje się w strefie rozciąganej
naprężenia ściskające występują w całej półce
wysokość strefy ściskanej jest mniejsza (lub równa) od wysokości półki
półka jest znacznie szersza (np. w stropie płytowo - żebrowym) ale do obliczeń musimy brać jedynie tzw. szerokość efektywną
Który z poniższych wzorów jest poprawny dla określenia obliczeniowej nośności podwójnie zbrojonego przekroju teowego (z półką w strefie ściskanej), w którym przekrój zbrojenia rozciąganego As1 jest równy przekrojowi zbrojenia ściskanego As2:
MRd=fyd*As1*(d-a2)
MRd=fyd*As2 *(d-a2)
MRd=As,lim*fyd*(d-a2)
MRd=As2*fyd*(d-a2)+(beff-bw)*hf*fcd*(d-0,5*hf)+eff,lim*bw*d2* fcd
MRd=As2*fyd*(d-a2)+(beff-bw)*hf*fcd*(d-0,5*hf)+eff*bw*d2* fcd
Skurcz w ściskanym elemencie żelbetowym powoduje:
wzrost naprężeń ściskających w betonie i spadek naprężeń rozciągających w stali,
spadek naprężeń ściskających w betonie i wzrost naprężeń ściskających w stali,
wzrost naprężeń ściskających w betonie i wzrost naprężeń rozciągających w stali,
wzrost naprężeń rozciągających w betonie i spadek naprężeń rozciągających w stali,
redystrybucję sił wewnętrznych w układach statycznie wyznaczalnych,
nie powoduje żadnych zmian w naprężeniach z wyjątkiem powstania rys skurczowych.
W przypadku małego mimośrodu w zbrojeniu o przekroju As1 występują naprężenia:
zawsze ściskające, których wartość jest mniejsza od granicy plastyczności stali
zawsze rozciągające, których wartość jest mniejsza od granicy plastyczności stali
ściskające lub rozciągające, których wartość jest zawsze mniejsza od granicy plastyczności stali
rozciągające, których wartość jest zawsze mniejsza od granicy plastyczności stali lub ściskające, których wartość jest mniejsza lub równa granicy plastyczności stali
Teowy pojedynczo zbrojony przekrój żelbetowy ma większą nośność gdy:
cała półka znajduje się w strefie naprężeń ściskających niż gdy znajduje się ona w strefie naprężeń rozciągających, przy tym samym przekroju zbrojenia
cała półka znajduje się w strefie naprężeń rozciągających niż gdy znajduje się ona w strefie naprężeń ściskających, przy tym samym przekroju zbrojenia,
Nośność pojedynczo zbrojonego przekroju teowego nie zależy od położenia półki
Wytrzymałość betonu na ściskanie jest:
zależna od prędkości przykładania obciążenia i wzrasta wraz ze wzrostem prędkości przykładania obciążenia
zależna od prędkości przykładania obciążenia i maleje wraz ze wzrostem prędkości przykładania obciążenia
jest niezależna od prędkości przykładania obciążenia.
Pełzanie w ściskanym elemencie żelbetowym powoduje:
wzrost naprężeń ściskających w betonie i spadek naprężeń rozciągających w stali,
spadek naprężeń ściskających w betonie i wzrost naprężeń ściskających w stali,
wzrost naprężeń ściskających w betonie i wzrost naprężeń rozciągających w stali,
wzrost naprężeń rozciągających w betonie i spadek naprężeń rozciągających w stali,
redystrybucję sił wewnętrznych w układach statycznie wyznaczalnych,
nie powoduje żadnych zmian w naprężeniach z wyjątkiem powstania rys skurczowych.
Obliczając, przy założeniu prostokątnego wykresu naprężeń w betonie ściskanym, nośność podwójnie zbrojonego przekroju zginanego, w sytuacji gdy xeff<2a2, stosujemy wzór MRd=fyd*As1*(d-a2), dlatego że:
wysokość strefy ściskanej betonu jest zbyt mała a czasami wręcz zerowa (np. przy As2=As1), aby można ją było uwzględniać,
wypadkowa naprężeń ściskających w betonie znajduje się w otulinie, która może odpadać i nie można dopuścić do tak wysokiego położenia tej wypadkowej,
naprężenia w stali ściskanej w opisywanej sytuacji nie osiągają granicy plastyczności fyd, stąd moment od siły Fs2 względem zbrojenia rozciąganego jest nieznany, bez dodatkowej analizy odkształceń
jest to jedynie jeden ze sposobów liczenia nośności, równie dobrze można byłoby ją obliczać stosując wzór: MRd=fyd*As2*(d-a2)
Z małym mimośrodem mamy do czynienia wtedy kiedy wymiarując przekrój mimośrodowo ściskany przy założeniu dużego mimośrodu okaże się, że:
As1 < 0,
As2 < 0,
As1 > As,lim,
As1 < As,min
Smukłość graniczna słupa jest to smukłość, powyżej której:
należy zawsze uwzględniać efekty II rzędu
słup należy traktować jako smukły
następuje niesygnalizowane wyboczenie słupa
spadek nośności słupa przekracza 50% w stosunku do nośności słupa krępego
słup niszczy się w sposób niesygnalizowany
Obliczając, przy założeniu prostokątnego wykresu naprężeń w betonie ściskanym, nośność podwójnie zbrojonego przekroju zginanego, w sytuacji gdy xeff<2a2, stosujemy wzór MRd=fyd*As1*(d-a2), dlatego że:
wysokość strefy ściskanej betonu jest zbyt mała a czasami wręcz zerowa (np. przy As2=As1), aby można ją było uwzględniać,
wypadkowa naprężeń ściskających w betonie znajduje się w otulinie, która może odpadać i nie można dopuścić do tak wysokiego położenia tej wypadkowej,
naprężenia w stali ściskanej w opisywanej sytuacji nie osiągają granicy plastyczności fyd, stąd moment od siły Fs2 względem zbrojenia rozciąganego jest nieznany, bez dodatkowej analizy odkształceń
jest to jedynie jeden ze sposobów liczenia nośności, równie dobrze można byłoby ją obliczać stosując wzór: MRd=fyd*As2*(d-a2)
Miarodajnymi przekrojami do wymiarowania słupa o węzłach przesuwnych są:
Przekroje przywęzłowe wymiarowane z uwzględnieniem smukłości (w przypadku słupa smukłego) i przekrój środkowy wymiarowany bez uwzględnienia smukłości
Przekroje przywęzłowe wymiarowane bez uwzględnienia smukłości i przekrój środkowy wymiarowany z uwzględnieniem smukłości (w przypadku słupa smukłego)
Tylko przekroje przywęzłowe wymiarowane z uwzględnieniem smukłości (w przypadku słupa smukłego)
Przekroje przywęzłowe i przekrój środkowy, wymiarowane z uwzględnieniem smukłości (w przypadku słupa smukłego)
Wraz ze wzrostem mimośrodu początkowego, wpływ smukłości na spadek nośności słupa
rośnie
maleje
pozostaje bez zmian
Wytrzymałość charakterystyczna betonu C25/30 na ściskanie wynosi:
30MPa
25MPa
25MPa:1,5
30MPa:1,4
25MPa/1,4
Graniczna wysokość strefy ściskanej zginanego przekroju żelbetowego jest:
większa w przypadku przekroju teowego niż prostokątnego
mniejsza w przypadku przekroju teowego niż prostokątnego
niezależna od kształtu przekroju
mniejsza w przypadku przekroju podwójnie zbrojonego niż pojedynczo zbrojonego
większa w przypadku przekroju podwójnie zbrojonego niż pojedynczo zbrojonego
W statycznie wyznaczalnej belce żelbetowej pełzanie powoduje:
Wzrost momentu przęsłowego i wzrost ugięć
Spadek momentu przęsłowego i spadek ugięć
Wzrost ugięć bez zmian momentów
Spadek ugięć bez zmian momentów.
Porównujemy dwa zginane przekroje pojedynczo zbrojone; prostokątny i teowy z półką znajdującą się w strefie ściskanej. Wysokość obu przekrojów jest identyczna. Szerokość środnika przekroju teowego jest identyczna jak szerokość przekroju prostokątnego. W obu porównywanych przekrojach położenie środków ciężkości zbrojenia rozciąganego jest identyczne. Co można powiedzieć o granicznym zbrojeniu rozciąganym As,lim w obu przekrojach?
Nic, dopóki się nie zna wartości momentu zginającego
As,lim w przekroju teowym będzie większe niż w przekroju prostokątnym
As,lim w przekroju prostokątnym będzie większe niż w przekroju teowym
As,lim w przekroju prostokątnym będzie identyczne jak w przekroju teowym
Porównujemy dwa przekroje; prostokątny i teowy z półką znajdującą się w strefie rozciąganej. Wysokość obu przekrojów jest identyczna. Szerokość środnika przekroju teowego jest identyczna jak szerokość przekroju prostokątnego. W obu porównywanych przekrojach identyczny jest przekrój zbrojenia, tak ściskanego jak i rozciąganego. Identyczne też jest położenie ich środków ciężkości. Co można powiedzieć o wysokości strefy ściskanej w fazie IIa obu przekrojów?
Nic, dopóki się nie zna wartości momentu zginającego
Wysokość xII w przekroju teowym będzie większa niż w przekroju prostokątnym
Wysokość xII w przekroju prostokątnym będzie większa niż w przekroju teowym
Wysokość xII w przekroju prostokątnym będzie identyczna jak w przekroju teowym
Który z poniższych wzorów jest poprawny dla określenia obliczeniowej nośności MRd mimośrodowo ściskanego przekroju prostokątnego, w którym przy zadanej sile ściskającej NEd wysokość strefy ściskanej, przy założeniu prostokątnego wykresu naprężeń w tej strefie, jest mniejsza niż 2* a2:
MRd=fyd*As2 *(d-a2)
MRd=fyd*As1*(d-a2)
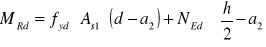
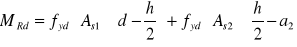
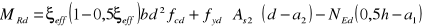
Graniczny przekrój zbrojenia pojedynczo zbrojonego zginanego przekroju teowego, o określonej geometrii, jest:
niezależny od położenia półki
większy w przypadku gdy półka znajduje się w strefie naprężeń ściskających
większy w przypadku gdy półka znajduje się w strefie naprężeń rozciągających
Moment zginający, powodujący zarysowanie przekroju teowego, o określonej geometrii, jest:
większy w przypadku gdy półka znajduje się w strefie naprężeń rozciągających
większy w przypadku gdy półka znajduje się w strefie naprężeń ściskających
niezależny od położenia półki
Określ wartość logiczną następujących zdań:
Skurcz w betonie rozpoczyna się z chwilą rozdeskowania elementu
Po przekroczeniu granicznego stopnia zbrojenia nośność przekroju nie zwiększa się
W betonach wysokiej wytrzymałości obserwuje się mniejsze pełzanie w porównaniu z betonami zwykłymi
W chwili zarysowania następuje wzrost wysokości strefy ściskanej przekroju
Ecm, którego wartość podawana jest w normie żelbetowej, i który jest wykorzystywany m. in. w analizie naprężeń liniowych zginanego przekroju żelbetowego (faza Ia i IIa) oznacza:
tzw. średni moduł początkowy betonu
tzw. średni moduł sieczny betonu równy tangensowi kąta nachylenia do osi odkształceń prostej przechodzącej przez punkty na krzywej σc -c o wartościach 0,4fc i 0,6fc
tzw. średni moduł sieczny betonu równy tangensowi kąta nachylenia do osi odkształceń prostej przechodzącej przez początek układu współrzędnych i punkt na krzywej σc -c o wartości 0,4fc
tzw. średni moduł styczny betonu równy tangensowi kąta nachylenia do osi odkształceń prostej stycznej do krzywej σc -c w punkcie o wartości 0,4fc
tzw. średni moduł styczny betonu równy tangensowi kąta nachylenia do osi odkształceń prostej stycznej do krzywej σc -c w punkcie o wartości 0,6fc
Ec,eff jest:
efektywnym siecznym modułem betonu obciążonego w sposób długotrwały, z uwzględnieniem czasu przyłożenia i trwania obciążenia
efektywnym stycznym modułem betonu, z uwzględnieniem parabolicznego wykresu naprężeń w strefie ściskanej
efektywnym siecznym modułem betonu po zarysowaniu, z uwzględnieniem współpracy betonu na odcinku między rysami (tzw. tension stiffening)
efektywnym modułem sprężystości betonu uwzględniającym fakt jego degradacji (zmniejszenia) wskutek nieliniowej zależności między odkształceniami a naprężeniami w betonie przy dużych poziomach obciążenia
jest efektywnym modułem sprężystości uwzględniającym wiek betonu w analizowanej chwili
Nośność tzw. przezbrojonego zginanego przekroju żelbetowego jest:
dużo większa (w zależności o stopnia przezbrojenia) od nośności przekroju nieprzezbrojonego, chociaż istnieje niestety niebezpieczeństwo niesygnalizowanego zniszczenia
nieco większa od nośności przekroju nieprzezbrojonego, ale istnieje niebezpieczeństwo niesygnalizowanego zniszczenia
równa nośności przekroju nieprzezbrojonego, ale w tym wypadku istnieje niebezpieczeństwo niesygnalizowanego zniszczenia
nieco mniejsza od nośności przekroju nieprzezbrojonego, a dodatkowo istnieje niebezpieczeństwo niesygnalizowanego zniszczenia
W przypadku tzw. małego mimośrodu (mimośrodowo ściskany przekrój żelbetowy) z całą pewnością można powiedzieć, że:
wysokość strefy ściskanej jest mniejsza od granicznej
strefa ściskana obejmuje cały przekrój
w zbrojeniu mniej ściskanym nie zostanie osiągnięta granica plastyczności
wysokość strefy ściskanej jest większa od granicznej
przekrój zbrojenia As1 jest ujemny i z tego względu zbrojenie to jest zbędne (przyjmuje się jedynie konstrukcyjnie)
3. W przypadku smukłości słupa mniejszej od smukłości granicznej pomija się wpływ efektów II rzędu, ponieważ:
mamy do czynienia ze słupem krępym, który pozostaje, bez względu na wielkość siły ściskającej, prosty (nie doznaje przemieszczeń poprzecznych)
wygięcie słupa nie przekracza wartości mimośrodu niezamierzonego
spadek nośności słupa w stosunku do nośności przekroju żelbetowego nie przekracza 10%
Po zarysowaniu teowego przekroju żelbetowego wysokość strefy ściskanej w przekroju przez rysę jest:
większa niż w przekroju między rysami
mniejsza niż w przekroju między rysami
identyczna jak w przekroju między rysami
większa lub mniejsza niż w przekroju między rysami w zależności od tego czy półka znajduje się w strefie ściskanej czy rozciąganej
Wysokość strefy ściskanej zginanego teowego przekroju żelbetowego w fazie IIa, wraz ze wzrostem momentu zginającego:
zwiększa się
zmniejsza się
pozostaje niezmienna
zwiększa się lub zmniejsza w zależności od tego czy półka znajduje się w strefie ściskanej czy rozciąganej
Przyjmuje się wartość współczynnika Poissona dla betonu równą 0,2 ale wiadomo, że jego wartość jest:
większa dla betonów wyższych wytrzymałości niż dla betonów niższych wytrzymałości
mniejsza dla betonów wyższych wytrzymałości niż dla betonów niższych wytrzymałości
równy jeden
jest stała przy obciążeniach do ok. 80% obciążenia niszczącego a następnie rośnie wraz ze wzrostem obciążenia
jest stała przy obciążeniach do ok. 80% obciążenia niszczącego a następnie maleje wraz ze wzrostem obciążenia
W przypadku gdy wysokość umownej strefy ściskanej w zginanym przekroju żelbetowym, podwójnie zbrojonym jest mniejsza od podwójnej odległości najbardziej ściskanego włókna betonu od środka ciężkości zbrojenia ściskanego, przyjmuje się założenie, że:
naprężenia ściskające przejmuje tylko zbrojenie, zaś beton nie bierze udziału w przenoszeniu naprężeń
linia działania wypadkowej naprężeń ściskających w betonie pokrywa się z linią działania wypadkowej naprężeń ściskających w zbrojeniu
przekrój zbrojenia ściskanego ma wartość zero
nie istnieje związek między wytrzymałością na rozciąganie a wytrzymałością na ściskanie
Skurcz betonu rozpoczyna się z chwilą:
połączenia (wymieszania) wszystkich składników mieszanki betonowej
rozpoczęcia procesu hydratacji
upływu 28 dni od ułożenia betonu
rozdeskowania elementu
zaprzestania pielęgnacji betonu
Przy identycznej geometrii (wymiary, przekrój zbrojenia i jego rozmieszczenie w przekroju) i identycznych właściwościach mechanicznych betonu i stali, nośność mimośrodowo ściskanego przekroju żelbetowego będzie:
większa w przypadku tzw. „małego mimośrodu” niż „dużego mimośrodu”
mniejsza w przypadku tzw. „małego mimośrodu” niż „dużego mimośrodu”
identyczna w obu przypadkach, jedynie w przypadku „małego mimośrodu” będziemy mieć do czynienia z niesygnalizowanym mechanizmem zniszczenia
Określ wartość logiczną następujących zdań:
pełzanie zależy od wieku betonu w chwili obciążenia, im później tym pełzanie jest mniejsze
wzrost ilości cementu w m3 betonu, przy niezmiennym stosunku w/c powoduje wzrost skurczu i spadek pełzania
w betonach wysokiej wytrzymałości obserwuje się mniejszy skurcz autogeniczny i wyższy skurcz od wysychania, w porównaniu z betonami zwykłymi
wzrost temperatury otoczenia powoduje wzrost skurczu i spadek pełzania
Wytrzymałość średnia betonu na ściskanie jest:
Większa od wytrzymałości obliczeniowej a mniejsza od charakterystycznej
Większa od wytrzymałości charakterystycznej i obliczeniowej
Mniejsza od wytrzymałości obliczeniowej i charakterystycznej
Wytrzymałość średnia betonu na ściskanie jest:
Większa od wytrzymałości obliczeniowej a mniejsza od charakterystycznej
Większa od wytrzymałości charakterystycznej i obliczeniowej
Mniejsza od wytrzymałości obliczeniowej i charakterystycznej
Określ wartość logiczną następujących zdań:
pełzanie zależy od wieku betonu w chwili obciążenia, im później tym pełzanie jest mniejsze
wzrost ilości cementu w m3 betonu, przy niezmiennym stosunku w/c powoduje wzrost skurczu i spadek pełzania
w betonach wysokiej wytrzymałości obserwuje się mniejszy skurcz autogeniczny i wyższy skurcz od wysychania, w porównaniu z betonami zwykłymi
wzrost temperatury otoczenia powoduje wzrost skurczu i spadek pełzania
10.01.2015
Egzamin z konstrukcji betonowych - VIs Budownictwo inż.,
studia stacjonarne i niestacjonarne (odpowiedzi na pytania 11 - 15)
Imię, Nazwisko, nr indeksu, nr grupy dziekańskiej (DRUKOWANIMI LITERAMI)
Wyszukiwarka
Podobne podstrony:
P MGR II 2015 Sprężone, Studia PG, Semestr 09 (Konstrukcje Betonowe), Konstrukcje Sprężone, Egzamin
Przykładowe pytania egzaminacyjne MGR II 2014-1, Studia PG, Semestr 09 (Konstrukcje Betonowe), Inżyn
EGZAMIN Z KONSTRUKCJI BETONOWYCH 2008 2009, Studia PG, Semestr 06, Konstrukcje Betonowe VI, Egzamin
hyd sciaga egzamin, Studia PG, Semestr 05, Hydraulika i Hydrologia, Egzamin
hydro-egzamin-wype B3nione-poprawione, Studia PG, Semestr 05, Hydraulika i Hydrologia, Egzamin
HYDRA, Studia PG, Semestr 05, Hydraulika i Hydrologia, Egzamin
HYDRAU~1 (2), Studia PG, Semestr 05, Hydraulika i Hydrologia, Egzamin
test - pytania (2), Studia PG, Semestr 05, Hydraulika i Hydrologia, Egzamin
pytania 70 - 80 żelbet, Studia PG, Semestr 06, Konstrukcje Betonowe VI, Egzamin
obliczenia, STUDIA, Polibuda - semestr IV, Konstrukcje Betonowe, Projekt, PŁYTA, sem v
Konstrukcje betonowe projekt, STUDIA, Polibuda - semestr IV, Konstrukcje Betonowe, Projekt, PŁYTA
pytaniaZybury, Studia Mgr, I semestr mgr, Konstrukcje Betonowe
Żelbet - Egzamin - Zagadnienia, Budownictwo S1, Semestr IV, Konstrukcje betonowe, Egzamin
Żelbet - Egzamin - Rysy i ugięcia, Budownictwo S1, Semestr IV, Konstrukcje betonowe, Egzamin
Żelbet - Egzamin - Definicje, Budownictwo S1, Semestr IV, Konstrukcje betonowe, Egzamin
betony - odpowiedzi, Studia PG Budownictwo, BUDOWNICTWO, SEMESTR V, KONSTRUKCJE BETONOWE, Egzamin
Metoda trójkatów, Studia PG, Semestr 05, TiORB, Ćwiczenia
Zagadnienia zaliczenie, Studia PG, Semestr 08, Fundamenty Specjalne, Egzamin
sprawko cement hanula, Studia PG, Semestr 04, Technologia betonów, Laboratorium, Sprawozdania
więcej podobnych podstron