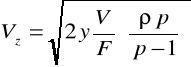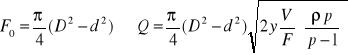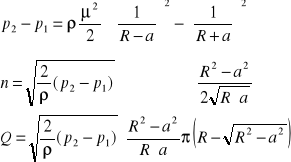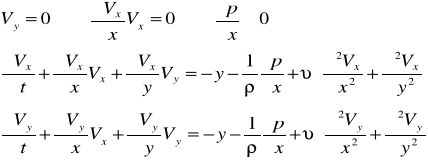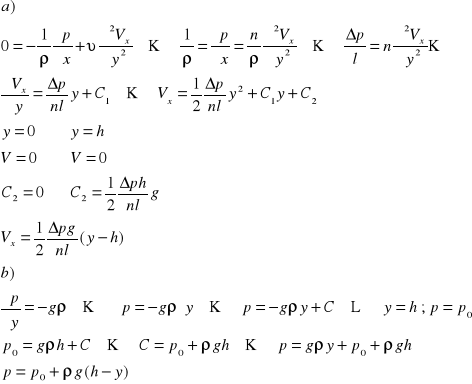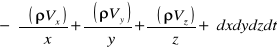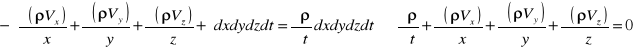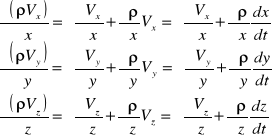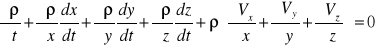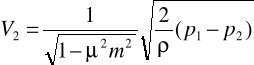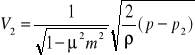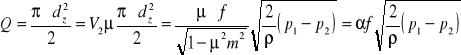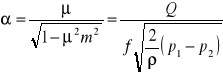1. pomiar strumienia objętości -przepływomierz pływakowy (rotometr) przepływ płynu odbywa się ku górze. Pomiar strumienia objętości rotometru sprowadza się do określenia położenia pływaka w kanale. Vz=√[(2Δp)/ρ] - z równ. Bernoulliego Δp - różnica ciśnień dla dolnej i górnej powierzchni pływaka. ΔpF + Vρy = Vyp - w stanie ustalonym 0 = Vz - F0 V - objętość pływaka ρ - gęstość płynu F - pole pow. pływaka F0 - swobodny przekrój szczeliny między pływakiem a ścianką kanału , gdy ρ=const Q=(π/4)*(D²-d²). -przepływ krzywakowy pomiar strumienia objętości za pomocą tego przyrządu polega na pomiarze różnicy ciśnień między strumieniami płynu opływowego. Wypukłą i wklęsłą stronę zakrywa przewód. Przy przepływie płynu przez zakrzywiony przewód na skutek działania siły dośrodkowej następuje wzrost ciśnienia w kierunku odśrodkowym. Różnica ciśnień po stronie wklęsłej i wypukłej krzywaka jest większa, im większy jest strumień m objętości przepływu krzywaka, jakościowo zbliżony jest do ruchu płynu idealnego, w którym moment prędkości M jest stały dla wszystkich elementów. R - promień krzywizny linii środkowej. r1=R-a r2=R+a {promienie zewnętrzne i wewnętrzne krzywaka} p2 - p1=[(V1^2-V2^2)/2]*ρ V1=μ/r1 ; V2=μ/r2 -przepływomierz końcowy (gazometr) W obudowie przepływomierza znajdują się dwa ruchome przewody z części komory zaworowej na stałą przegrodę dzielące przewód na dwie identyczne części. Przy otwartych zaworach wlotowych i zamkniętych wylotowych następuje napełnienie komór powietrzem. Wielkością pomiarową gazomierza jest wielkość skokowa komór.	11 płyty nieprzesuwne - wzór Nomera - Stokesa
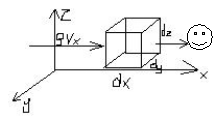
12 równanie ciągłości - ruch nieustalony płynu ściśliwego Przy przepływie przestrzennym, gdzie wyznaczamy składowe prędkości Vx,Vy,Vz ciśnienie p i ρ jako funkcję współrzędnych x, y, z równania ciągłości wyprowadza się z równania masy płynu, która wypływa z elementarnego sześcianu o krawędziach dx, dy, dz . ☺- Nieustawny przepływ płynu ściśliwego gdzie gęstość ρ(x, y, z, t)=0. W czasie dt w kierunku osi x wpływa do elementu przez lewą ścianę o powierzchni dydz masa płynu ρVxdzdydt. Przez przeciwległą ściankę w tym samym czasie wypływa masa płynu. przyrost masy w czasie dt w kierunku osi x Analogicznie przyrost masy przy przepływie w kierunku y i z wynoszą: Suma przyrostów mas w elemencie płynu w kierunku wszystkich osi: Równocześnie jednak mamy gęstość ρ która w czasie t wynosiła ρ(x,y,z,t), więc w czasie t+dt gęstość ρ(x,y,z,t+dt)=ρ+(لρ/لt)*dt W czasie dt masa płynu wewnątrz elementu zmieni się od wartości ρ(dxdydz) do [ρ(لρ/لt)*dt]dxdydz. Stąd przyrost masy -ρdxdydz+[ρ+(لρ/لt)*dt]dxdydz = (لρ/لt)dxdydzdt. Porównując przyrosty otrzymujemy: {różnicowe równanie ciągłości ruchu nieustalonego płynu ściśliwego. lub : Podstawiając do równania ciągłości : → równanie ciągłości ruchu nieustalonego płynu ściśliwego.	13. Dysza zwężka Venturiego Dysza Venturiego jest to dysza z długim dyfuzorem, czyli takim, gdzie większa średnica dyfuzora równa jest średnicy przewodu a otwory impulsowe znajdują się po stronie dopływu w obudowie dyszy a po stronie odpływu w cylindrycznym przewężeniu. Jeżeli zastosujemy zwężkę w rurociągu to spowoduje ona zmniejszenie przekroju poprzecznego a co za tym idzie wzrost średniej prędkości przepływu i energii kinetycznej oraz spadek ciśnienia statycznego. Jeżeli płyn ma gęstość stałą i porusza się w kierunku poziomym rurociągu to równanie Bernoulliego będzie miało postać : V1²/2 + p1/ρ = V2²/2 + p2/ρ Stopień rozwarcia modułu zwężki „m”=(d/Δ)² a stopień przewężenia strumienia m=(d/Δ)². Z równania ciągłości wynika V1=V2=F2/F1 → V2=μm. Prędkość przepływu płynu idealnego wynosi : W przepływie rzeczywistym ρ<<1 Strumień objętości wynosi : Gdzie : α - liczba przepływu zwężki, f - pole powierzchni przekroju zwężki.

---