Pracownia Zakładu Fizyki Technicznej Politechniki Lubelskiej

Nazwisko i imię studenta: OLESZCZUK MARIUSZ						Symbol grupy: WT 3.3
Data wyk. Ćwiczenia : 1998-01-14		Symbol ćwiczenia: 6.1		Temat zadania: Wyznaczanie elementów LC obwodu metodą rezonansu
	ZALICZENIE			Ocena:	Data:	Podpis:

1.Cel ćwiczenia:

Celem ćwiczenia jest zapoznanie się z metodą pomiaru wartości indukcyjności i pojemności.

2.Zagadnienia teoretyczne:

Najczęściej występującymi elementami w obwodach elektrycznych są: rezystancja R, pojemność C oraz indukcyjność L.

Pojemność wzajemna dwóch przewodników jest wielkością fizyczną równą liczbowo wartości ładunku elektrycznego jaki należy przenieść z jednego przewodnika na drugi, aby napięcie między nimi zmieniło się o jednostkę:

Pojemność elektryczna układu przewodników zależy od ich kształtów, rozmiarów, wzajemnego położenia oraz od własności elektrycznych środowiska, w którym się one znajdują. Najprostszym kondensatorem jest kondensator płaski, którego pojemność wyraża się wzorem:

gdzie jest przenikalnością dielektryczną izolatora znajdującego się pomiędzy płytkami kondensatora.

Indukcyjność L jest wielkością fizyczną charakteryzującą zdolność obwodu elektrycznego do wytwarzania SEM samoindukcji. SEM samoindukcji pojawia się w obwodzie zawsze, gdy w obwodzie natężenie prądu ulega zmianie:

E_s=L

W układzie SI jednostką indukcyjności jest jeden Henr.

Indukcyjność jest wielkością stałą dla danego obwodu elektrycznego, jej wartość związana jest jedynie z geometrycznymi rozmiarami obwodu i własnościami magnetycznymi środowiska, w którym ten obwód się znajduje.

Idealny obwód drgający zawiera tylko elementy L i C (R=0). Po naładowaniu kondensatora do napięcia U₀, w obwodzie popłynie okresowo zmienny prąd o natężeniu:

i=i₀sin(ω₀-).

Gdzie i₀ jest amplitudą natężenia prądu, związaną z napięciem U₀ zależnością:

i₀=.

Wielkość ω₀ jest pulsacją drgań swobodnych obwodu, określoną wzorem Thomsona:

ω₀=.

W rzeczywistych obwodach drgających rezystancja R nie jest równa zeru, toteż występują w nim straty energetyczne, związane z wydzielaniem się ciepła i stanowiące przyczynę zanikania prądu elektrycznego. W celu podtrzymania przepływu prądu, należy włączyć do obwodu zewnętrzne źródło energii elektrycznej o sile elektromotorycznej okresowo zmiennej np.: E=E₀sinωt , wówczas chwilową wartość natężenia prądu opisuje równanie:

i(t)=i₀ sin(ωt-ϕ) ,

w którym amplituda wynosi:

i₀=.

Z powyższego wzoru wynika, że w danym obwodzie RLC, amplituda natężenia prądu osiąga wartość maksymalną:

i_0max=,

jeżeli pulsacja zewnętrznej SEM będzie równa wartości ω_r , spełniającej warunek :

Wielkość ω_r nazywamy pulsacją rezonansową. Łatwo zauważyć, że wartość pulsacji rezonansowej jest równa pulsacji drgań własnych obwodu i wynosi:

Zjawisko występowania maksymalnej amplitudy natężenia prądu w obwodzie RLC, przy pulsacji sem równej pulsacji drgań własnych obwodu, nosi nazwę - rezonansu elektrycznego.

W przypadku rezonansu, przesunięcie fazowe ϕ między natężeniem prądu a sem jest równe zeru, natomiast chwilowe wartości napięć na poszczególnych elementach

wynoszą:

3.Wykonanie ćwiczenia:

W celu wykonania ćwiczenia zestawiamy obwód jak niżej, składający się z cewki , której indukcyjność L_x należy wyznaczyć, kondensatora wzorcowego o pojemności C₀ i miliamperomierza. Źródłem zasilania jest generator drgań sinusoidalnych G o regulacji częstotliwości ν.

L_x , R_x

G C_o

A

Wł.

Wartości L_x obliczamy ze wzorów:

4.Wyniki pomiarów:

wyniki:

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27
ν	500	550	600	650	700	750	800	850	900	950	1000	1050	1100	1150	1200	1250	1300	1350	1400	1450	1500	1550	1600	1650	1700	1750	1800
I	48.6	53.1	56.2	58.7	60.7	62.2	63.2	64	64.4	64.6	64.2	64	63.6	62.9	62.1	61.3	60.3	59.3	58.3	57.4	56.2	55.2	54.1	53.1	52.1	51.1	50.1

C_o=3μF ν_r=950 Hz L_x=0.0094H

Nr	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27
ν	500	550	600	650	700	750	800	850	900	950	1000	1050	1100	1150	1200	1250	1300	1350	1400	1450	1500	1550	1600	1650	170	1750	1800
I	44.9	48.5	51.7	54.5	57	59.2	59.4	60.7	61.6	62.3	62.7	62.9	63.2	63	63	62.4	61.9	61.1	59.8	58.5	57.2	56.3	55.2	54.2	53.2	52.3	51.1

C₀=2.7μF ν_r=950Hz L_x2=0.010H

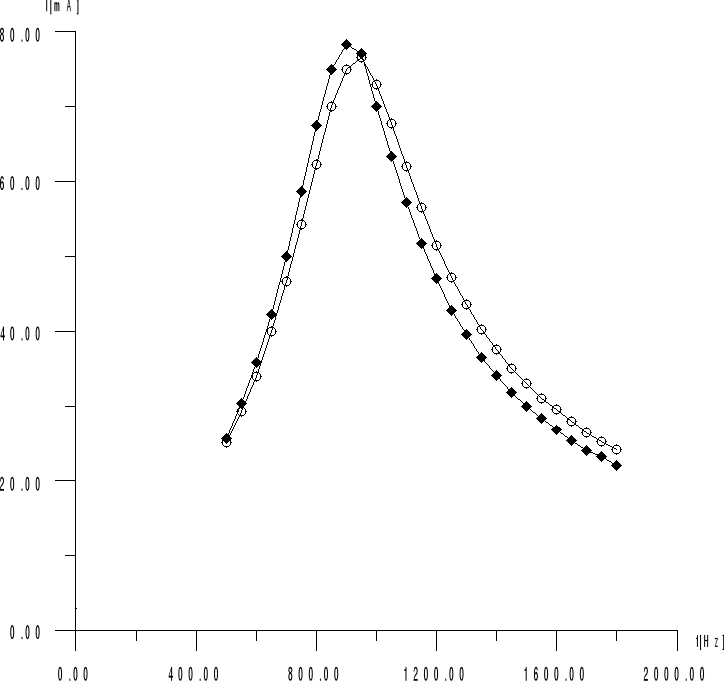
4.Rachunek błędu:

dla C=2.5μF : ΔC₀=(1%*11μF/100%)+(0.5%*1.1μF/100%)=0.000000016

Δν=0.01

ν=950Hz

(0.000021+0.005333)*100%=0.54%.

(0.000019+0.002)*100%=0.2%

---