Zestaw I

1. Na podstawie próbki wstępnej pobranej z węgla klasy 70-80 mm uzyskano zawartości popiołu w ziarnach: 10,1; 9,0; 11,3; 10,7; 11,4; 8,7; 11,0; 9,8. Wyznacz potrzebną do pobrania liczbę ziaren aby ocena średniej zawartości popiołu była podana z dokładnością 1%, skalkuluj masę dodatkowej próbki, jeżeli średnia gęstość ziarna badanej klasy wynosi 1450 g/m³.

Z tablicy nr 6 dla
t_α=3,499

Podstawiamy do wzoru na wyznaczanie minimalnej wartości próby z małej próbki (model II)

Gdzie d - błąd pomiarów u nas 0,01; s - odchylenie kwadratowe s² = 1,05

s² =
- dla małej próbki max. 30

Xi	xi-xśr	(xi-xśr)^2	Xśr	s2 (wariancja)	n
10,1	-0,15	0,0225	10,25	1,05428571	129076,2
9	-1,25	1,5625
11,3	1,05	1,1025
10,7	0,45	0,2025
11,4	1,15	1,3225
8,7	-1,55	2,4025
11	0,75	0,5625
9,8	-0,45	0,2025
		7,38

Co najmniej potrzeba n=129077, czyli potrzebujemy jeszcze y=n-8 pomiarów.

Nie wiem jak wygląda wzór z normy bo nie umie jej nigdzie dostać

Masa dodatkowej próby
0 [kg]

Gdzie V - objętość średniej próbki (należy przyjąć, że próbka ma kształt np. kuli V=4/3πr³)

2. Opróbowano dwa strumienie koncentratów węgla (z dwóch zakładów). Uzyskano następujące wyniki zawartości popiołu w węglu:

Zakład I : 10,8; 11,9; 16,2; 15,3; 14,7; 12,8; 11,9.

Zakład II: 12,1; 14,5; 17,0; 13,3; 12,9; 13,8; 15,1; 16,0; 13,1.

Zweryfikować hipotezę, że zakłady produkują koncentraty o jednakowych zawartościach (test serii, poziom istotności = 0,05).

H₀: zakłady produkują koncentraty o jednakowych zawartościach popiołu w węglu

H₁: zakłady produkują koncentraty o różnych zawartościach popiołu w węglu

Układamy liczby w jeden ciąg od najmniejszej do największej ( liczbą z zakładu I przypisujemy A, liczbą z zakładu II przypisujemy B (test serii, model II)

A	A	A	B	A	B	B	B	B	B	A	B	A	B	A	B
10,8	11,9	11,9	12,1	12,8	12,9	13,1	13,3	13,8	14,5	14,7	15,1	15,3	16,0	16,2	17,0

Otrzymaliśmy k=10 serii: AAA B A BBBBB A B A B A B n_A=7 i n_B=9

Poziom istotności α = 0,05

k_α odczytujemy z tablicy 15 dla n_A=7, n_B=9, α = 0,05 k_α =5

k > k_α→ H₀ przyjmujemy

3. Mając krzywą składu ziarnowego (dystrybuantę) zadaną tabelą, podaj przybliżone wartości wychodów:

1. klasy (0; 0,5);

2. klasy (0,8; 1,5);

3. klasy powyżej 2 mm.

Klasy [mm]	Φ(d)
(0; 0,1) (0,1; 0,5) (0,5; 1) (1; 2) (2; 3) (3; 5)	8 15 25 36 61 75

Narysuj krzywe składu ziarnowego o przewadze ziaren drobnych; grubych; o braku wybranej klasy.

4. Wyznaczając liniowe równanie regresji y=ax+b otrzymano wartość a=1,75 oraz s_x=3,35 i s_y=5,5, n=27. Oceń istotność równania i przyjmując b=3 wyznacz wartość y dla x=3.

Wyznaczenie wsp korelacji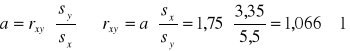
korelacja nie może być wyższa niż 1! ( współczynnik korelacji liniowej Pearsona ma zawierać się: r_xyϵ<-1,1>)

i
to jest test zgodności dla współczynnika korelacji t = obliczone porównujemy z t z tablic t-studenta dla s=27-2=25

i szukamy takiej liczby t_s w tablicach dla której t wyliczone jest mniejsze

dla t=0,477 t_s= 5,31 z tego wynika że prosta jest przyporządkowana w istotności równej 0,6 ale to sa domysły druga część jest prosta

y=1,75*3+3

y=8,25

5. Stosując test mediany odpowiedz na pytanie czy badane węgle pochodzą z tego samego pokładu

Wyniki	Próba I	Próba II
>me	38	12
<me	15	25

		próba 1				próba 2		ni	pi
			29,44444				20,55556
>me		38				12		50	0,555556
	0,32716			0,228395
			23,55556				16,44444
<me		15				25		40	0,444444
	0,261728			0,182716
Nj		53				37		90
Pj		0,588889				0,411111
Pij		npij		nij-npij			(nij-npij)^2		(nij-npij)^2/npij
0,32716		29,44444		8,555556			73,19753		2,485954
0,228395		20,55556		-8,55556			73,19753		3,560961
0,261728		23,55556		-8,55556			73,19753		3,107442
0,182716		16,44444		8,555556			73,19753		4,451201
								Σ=	13,60556
	chi2 =	13,60556
	chi2 alfa = 10,827
	13,605 > 10,827
	Ho odrzucamy. Węgle nie pochodzą z tego samego pokładu.

6. Podaj własne przykłady zastosowania statystyki w życiu lub w naukach górniczych.

Oszacowanie wydajności na danych zmianach roboczych + j/w

Przykładów można znaleźć tysiące tylko jest pytanie czy mamy podać jakiś konkretny przykład np. wymyślony z tokiem rozwiązania?

7. Zdefiniuj pojęcia: moda, mediana, współczynnik ufności, kwartyl dolny.

Moda- to taka wartość zmiennej która w całej zbiorowości powtarza się najczęściej.

Mediana- w celu jej wyznaczenia należy uporządkować rosnąco wartości zmiennej i ustalić która z nich zajmuje miejsce centralne - wartość tej zmiennej będzie wartością mediany. Mediana jest tą wartością zmiennej której odpowiada liczebność skumulowana do jednostki o numerze N/2 włącznie.

Kwartyl górny-jest wartością zmiennej która w uporządkowanym szeregu zajmuje pozycję 3N/4

Kwartyl dolny- jest wartością zmiennej która w uporządkowanym szeregu zajmuje pozycję N/4

Poziom istotności- jest to maksymalne dopuszczalne prawdopodobieństwo popełnienia błędu pierwszego rodzaju ( oznaczane symbolem α). Określa tym samym maksymalne ryzyko błędu, jakie badacz jest skłonny zaakceptować.

Współczynnik ufności- Prawdopodobieństwo z którym chcemy poznać prawdziwe położenie wybranych parametrów statystycznych. Zaznacza się je jako (1-α) i określa jako 100(1-α)- procentowy przedział ufności.