Zestaw I
Na podstawie próbki wstępnej pobranej z węgla klasy 70-80 mm uzyskano zawartości popiołu w ziarnach: 10,1; 9,0; 11,3; 10,7; 11,4; 8,7; 11,0; 9,8. Wyznacz potrzebną do pobrania liczbę ziaren aby ocena średniej zawartości popiołu była podana z dokładnością 1%, skalkuluj masę dodatkowej próbki, jeżeli średnia gęstość ziarna badanej klasy wynosi 1450 g/m3.
Z tablicy nr 6 dla
tα=3,499
Podstawiamy do wzoru na wyznaczanie minimalnej wartości próby z małej próbki (model II)
Gdzie d - błąd pomiarów u nas 0,01; s - odchylenie kwadratowe s2 = 1,05
s2 = ![]()
- dla małej próbki max. 30
Xi |
xi-xśr |
(xi-xśr)^2 |
Xśr |
s2 |
n |
10,1 |
-0,15 |
0,0225 |
10,25 |
1,05428571 |
129076,2 |
9 |
-1,25 |
1,5625 |
|
|
|
11,3 |
1,05 |
1,1025 |
|
|
|
10,7 |
0,45 |
0,2025 |
|
|
|
11,4 |
1,15 |
1,3225 |
|
|
|
8,7 |
-1,55 |
2,4025 |
|
|
|
11 |
0,75 |
0,5625 |
|
|
|
9,8 |
-0,45 |
0,2025 |
|
|
|
|
|
|
|
|
|
Co najmniej potrzeba n=129077, czyli potrzebujemy jeszcze y=n-8 pomiarów.
Nie wiem jak wygląda wzór z normy bo nie umie jej nigdzie dostać
Masa dodatkowej próby
0 [kg]
Gdzie V - objętość średniej próbki (należy przyjąć, że próbka ma kształt np. kuli V=4/3πr3)
Opróbowano dwa strumienie koncentratów węgla (z dwóch zakładów). Uzyskano następujące wyniki zawartości popiołu w węglu:
Zakład I : 10,8; 11,9; 16,2; 15,3; 14,7; 12,8; 11,9.
Zakład II: 12,1; 14,5; 17,0; 13,3; 12,9; 13,8; 15,1; 16,0; 13,1.
Zweryfikować hipotezę, że zakłady produkują koncentraty o jednakowych zawartościach (test serii, poziom istotności = 0,05).
H0: zakłady produkują koncentraty o jednakowych zawartościach popiołu w węglu
H1: zakłady produkują koncentraty o różnych zawartościach popiołu w węglu
Układamy liczby w jeden ciąg od najmniejszej do największej ( liczbą z zakładu I przypisujemy A, liczbą z zakładu II przypisujemy B (test serii, model II)
A |
A |
A |
B |
A |
B |
B |
B |
B |
B |
A |
B |
A |
B |
A |
B |
10,8 |
11,9 |
11,9 |
12,1 |
12,8 |
12,9 |
13,1 |
13,3 |
13,8 |
14,5 |
14,7 |
15,1 |
15,3 |
16,0 |
16,2 |
17,0 |
Otrzymaliśmy k=10 serii: AAA B A BBBBB A B A B A B nA=7 i nB=9
Poziom istotności α = 0,05
kα odczytujemy z tablicy 15 dla nA=7, nB=9, α = 0,05 kα =5
k > kα→ H0 przyjmujemy
Mając krzywą składu ziarnowego (dystrybuantę) zadaną tabelą, podaj przybliżone wartości wychodów:
klasy (0; 0,5);
klasy (0,8; 1,5);
klasy powyżej 2 mm.
Wyznaczając liniowe równanie regresji y=ax+b otrzymano wartość a=1,75 oraz sx=3,35 i sy=5,5, n=27. Oceń istotność równania i przyjmując b=3 wyznacz wartość y dla x=3.
Stosując test mediany odpowiedz na pytanie czy badane węgle pochodzą z tego samego pokładu
Podaj własne przykłady zastosowania statystyki w życiu lub w naukach górniczych.
Zdefiniuj pojęcia: moda, mediana, współczynnik ufności, kwartyl dolny.
Klasy [mm] |
Φ(d) |
(0; 0,1) (0,1; 0,5) (0,5; 1) (1; 2) (2; 3) (3; 5) |
8 15 25 36 61 75 |
Narysuj krzywe składu ziarnowego o przewadze ziaren drobnych; grubych; o braku wybranej klasy.
Wyznaczenie wsp korelacji 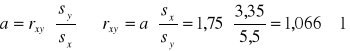
korelacja nie może być wyższa niż 1! ( współczynnik korelacji liniowej Pearsona ma zawierać się: rxyϵ<-1,1>)
i
to jest test zgodności dla współczynnika korelacji t = obliczone porównujemy z t z tablic t-studenta dla s=27-2=25
i szukamy takiej liczby ts w tablicach dla której t wyliczone jest mniejsze
dla t=0,477 ts= 5,31 z tego wynika że prosta jest przyporządkowana w istotności równej 0,6 ale to sa domysły druga część jest prosta
y=1,75*3+3
y=8,25
Wyniki |
Próba I |
Próba II |
>me |
38 |
12 |
<me |
15 |
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
próba 1 |
|
|
próba 2 |
|
ni |
pi |
|
|
|
|
|
29,44444 |
|
|
20,55556 |
|
|
|
|
>me |
|
38 |
|
|
12 |
|
50 |
0,555556 |
|
|
|
0,32716 |
|
|
0,228395 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23,55556 |
|
|
16,44444 |
|
|
|
|
<me |
|
15 |
|
|
25 |
|
40 |
0,444444 |
|
|
|
0,261728 |
|
|
0,182716 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Nj |
|
53 |
|
|
37 |
|
90 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pj |
|
0,588889 |
|
|
0,411111 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pij |
|
npij |
|
nij-npij |
|
(nij-npij)2 |
|
(nij-npij)2/npij |
||
|
|
|
|
|
|
|
|
|
|
|
0,32716 |
|
29,44444 |
|
8,555556 |
|
73,19753 |
|
2,485954 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,228395 |
|
20,55556 |
|
-8,55556 |
|
73,19753 |
|
3,560961 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,261728 |
|
23,55556 |
|
-8,55556 |
|
73,19753 |
|
3,107442 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,182716 |
|
16,44444 |
|
8,555556 |
|
73,19753 |
|
4,451201 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Σ= |
13,60556 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
chi2 = |
13,60556 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
chi2 alfa = 10,827 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
13,605 > 10,827 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Ho odrzucamy. Węgle nie pochodzą z tego samego pokładu. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
Oszacowanie wydajności na danych zmianach roboczych + j/w
Przykładów można znaleźć tysiące tylko jest pytanie czy mamy podać jakiś konkretny przykład np. wymyślony z tokiem rozwiązania?
Moda- to taka wartość zmiennej która w całej zbiorowości powtarza się najczęściej.
Mediana- w celu jej wyznaczenia należy uporządkować rosnąco wartości zmiennej i ustalić która z nich zajmuje miejsce centralne - wartość tej zmiennej będzie wartością mediany. Mediana jest tą wartością zmiennej której odpowiada liczebność skumulowana do jednostki o numerze N/2 włącznie.
Kwartyl górny-jest wartością zmiennej która w uporządkowanym szeregu zajmuje pozycję 3N/4
Kwartyl dolny- jest wartością zmiennej która w uporządkowanym szeregu zajmuje pozycję N/4
Poziom istotności- jest to maksymalne dopuszczalne prawdopodobieństwo popełnienia błędu pierwszego rodzaju ( oznaczane symbolem α). Określa tym samym maksymalne ryzyko błędu, jakie badacz jest skłonny zaakceptować.
Współczynnik ufności- Prawdopodobieństwo z którym chcemy poznać prawdziwe położenie wybranych parametrów statystycznych. Zaznacza się je jako (1-α) i określa jako 100(1-α)- procentowy przedział ufności.
Wyszukiwarka
Podobne podstrony:
Strona tytułowa - Word 2003, Prywatne, Studia
Liszka, materiały medycyna SUM, patomorfologia, pytania
kolokwium rok II 20070117, Prywatne, 1 SUM, infa, Matlab kurs pl (bd4ty3), matlab
Strona tytułowa - Word 2003, Prywatne, Studia
Statystyka SUM w4
ściąga statystyka, MEDYCYNA - ŚUM Katowice, I ROK, Biofizyka
zestaw zadań statystyka SUM GiG (1)
Przykładowe pytania ze statystyki (1), ochrona środowiska UJ, I semestr SUM, statystyka
1-14, ochrona środowiska UJ, I semestr SUM, statystyka
Zaliczenie dzienne statystyka 2 marca 2003 zadania, ZAD
2003.05.17 prawdopodobie stwo i statystyka
2003.12.06 prawdopodobie stwo i statystyka
2003 12 06 prawdopodobie stwo i statystykaid 21710
2003 05 17 prawdopodobie stwo i statystykaid 21698
Dane z policyjnego systemy statystyk TEMIDA (Przestępstwa seksualne) 2003 2009
statystyka word 2003, statystyka
dynamika word 2003, statystyka
swd 2003 all, wisisz, wydzial informatyki, studia zaoczne inzynierskie, statystyczne metody wspomaga
więcej podobnych podstron