Piotr Brzyski
Nr.127547
WPROWADZENIE DO SYSTEMÓW TELEKOMUNIKACYJNYCH
SEMINARIUM
I. Zadanie Z-2 / 15
Zaproponować układ który przekształci sygnał y(t) w falę zmodulowaną DSB-SC o pulsacji nośnej ϖo. Znaleźć amplitudę A o zmodulowanej fali nośnej na wyjściu układu. Narysować widmo S(ϖ).
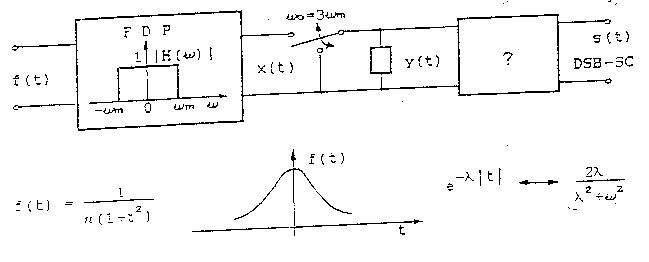
Wprowadzenie
Przy dwuwstęgowej modulacji amplitudy bez fali nośnej (DCB-SC Double SieBand- Suppressed Carrier) funkcja nośna ma postać fali harmonicznej cos(ω0t) , funkcjonał modulacji natomiast jest wprost sygnałem modulującym f(t). Zgodnie z wyrażeniem :
s(t)=c(t)⋅m[f(t)] sygnał zmodulowany jest iloczynem fali nośnej i sygnału modulującego:
s(t)=f(t) cos(ω0t)
W wyniku tej operacji widmo sygnału modulującego ulega przesunięciu ( zachowując swój kształt) o ±ω0 wzdłuż osi częstotliwości.
Rozwiązanie
Patrząc od końca układu otrzymamy sygnał modulujący s(t) , któremu odpowiada widmo
s(t)=f(t)⋅ cos(ω0t) ↔ ½⋅[ F(ω - ω0) + F(ω + ω0) ]
co odpowiada warunkom zadania
s(t) ↔ ½⋅[ Y(ω - 3⋅ωn) + Y(ω + 3⋅ωn) ]
gdzie Y(ω) - jest widmem amplitudowym sygnału y(t).
Sam sygnał x(t) jest sygnałem uzyskanym przez przepuszczenie sygnału f(t) przez filtr dolnoprzepustowy (FDP).
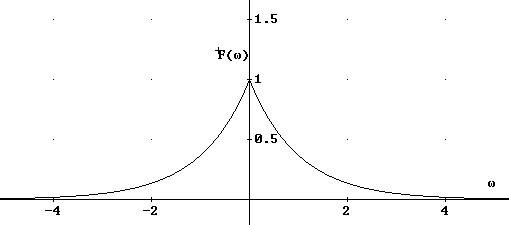
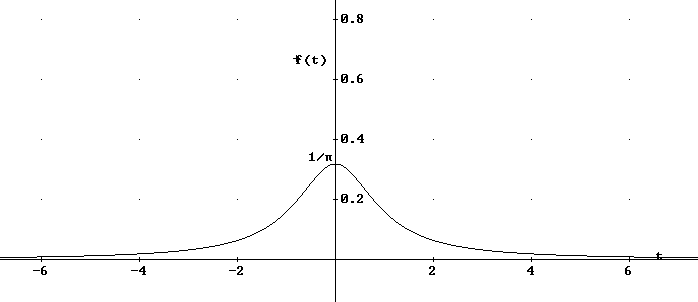
Korzystam z własności przekształcenia : f(t)⇔F(ω) to F(t)⇔2π⋅f(ω)
![]()
Ponieważ ![]()
, tak więc dla λ=1 mamy :
![]()
![]()
Idąc dalej
Zamieniając dziedziny
![]()
![]()
Czyli
Następnie wyznaczamy czasową i częstotliwościową postać h(t) i H(ω)
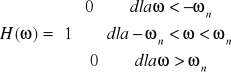
Natomiast h(t)= Sa(ωo⋅t) Sa(ωo⋅t)⇔![]()
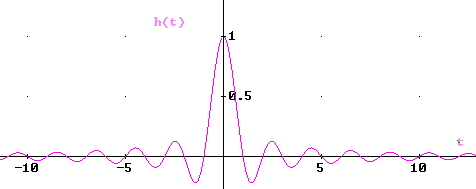
Po przejściu sygnału „ f ” przez filtr otrzymujemy :
![]()
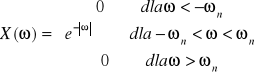
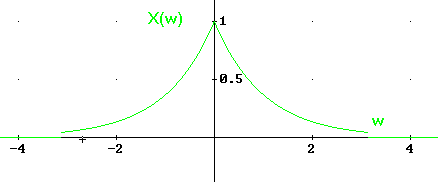
Co można przedstawić na wykresach w dwóch dziedzinach : czasu i częstotliwości
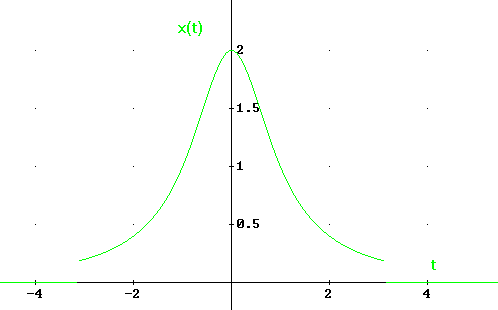
Następnie sygnał ten jest kluczowany przez q(t)
![]()
Co zgodnie z treścią zadania wynosi:
![]()
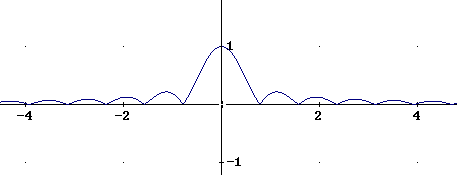
Rozpisując x(t) na nieskończony przebieg składowych sinusoidalnych otrzymujemy
![]()
co przedstawia się graficznie :
Transformatę natomiast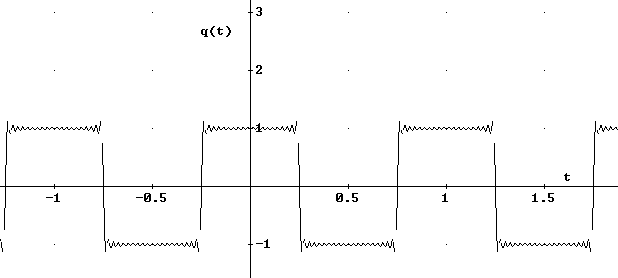
wyliczamy :
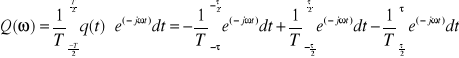
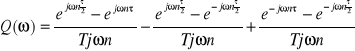
![]()
![]()
co ogólnie można zapisać
![]()
Tak więc y(t) jest kluczowanym sygnałem x(t) przez q(t) :
Mając postać czasową sygnału x(t) poddajemy go kluczowaniu , otrzymujemy sygnał y(t) , który przechodząc przez filtr dolnoprzepustowy o częstotliwości ω0=3ωn obcina wyższe częstotliwości które pojawiają się jak 3ω0=9ωn , 5ω0=15ωn , 7ω0=21ωn .....
![]()
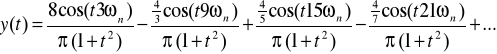
W tym miejscu potrzebny jest filtr który odfiltruje składowe o wyższej częstotliwości niż 3ωn w skutek czego na wyjściu otrzymamy sygnał
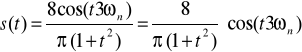
Sygnał s(t) złożyć można z fali nośnej c(t)=cos(t⋅3ωn) i sygnału modulującego y(t)'=m[f(t)]=![]()
Wnioski
Jak widać modulacja dwuwstęgowa ze stłumioną wstęgą boczną DSB-SC jest realizowalna przez układ z kluczowaniem ( możliwa też jest modulacja z modulatorem pierścieniowym ). Natomiast samo rozwiązanie okazuje się kłopotliwe , pojawiają się skomplikowane całki. Wyliczony sygnał s(t) jest sygnałem który pojawi się na wyjściu układu gdy zastosujemy filtr dolnoprzepustowy o częstotliwości ω0=3ωn. Przykładem takiego filtru może być filtr pokazany na rysunku z zastosowaniem wzmacniacza operacyjnego nie odwracającego fazy :
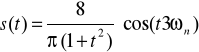
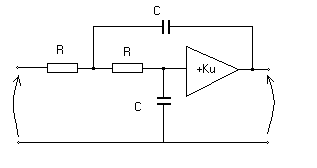
Wykres s(t) 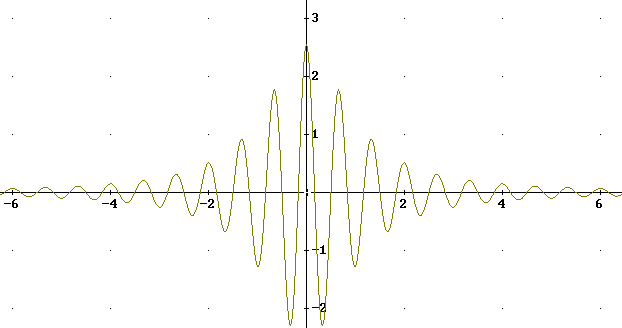
S(w) wyliczamy :
s(t) ↔ ½⋅[ Y(ω - 3⋅ωn) + Y(ω + 3⋅ωn) ]
![]()
gdzie Y(ω) - jest widmem amplitudowym sygnału y(t)'=m[f(t)]=![]()
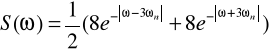
więc
wykres S(ω)
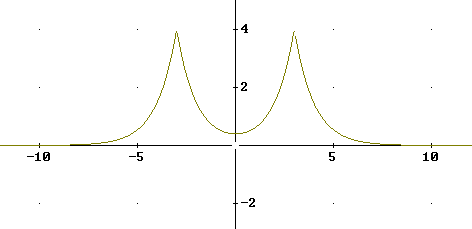
1
1
![]()
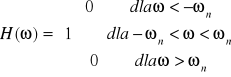
![]()
![]()
![]()
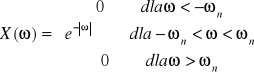
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
Z2 08, SPRAWOZDANIA czyjeś
z2 05, SPRAWOZDANIA czyjeś
z1 15, SPRAWOZDANIA czyjeś
z2 02, SPRAWOZDANIA czyjeś
z2 03, SPRAWOZDANIA czyjeś
Z2 11a, SPRAWOZDANIA czyjeś
z2 12, SPRAWOZDANIA czyjeś
z2 11, SPRAWOZDANIA czyjeś
Z2 04, SPRAWOZDANIA czyjeś
Z2 01a, SPRAWOZDANIA czyjeś
z 1 15 b, SPRAWOZDANIA czyjeś
15!, SPRAWOZDANIA czyjeś
z2 09, SPRAWOZDANIA czyjeś
pomoc2cd(1), SPRAWOZDANIA czyjeś
Budowa kontenera C, SPRAWOZDANIA czyjeś
Zalety systemów SDH, SPRAWOZDANIA czyjeś
Hartowanie i odpuszczanie, SPRAWOZDANIA czyjeś
z3 06, SPRAWOZDANIA czyjeś
więcej podobnych podstron