Uniwersytet Śląski WYDZIAŁ TECHNIKI Sosnowiec	SPRAWOZDANIE Z ZAJĘĆ LABORATORYJNYCH	Kierunek WT	Semestr II	Sprawdził
					Data wyk. Ćwiczenia 7.0.0r.
INSTYTUT PROBLEMÓW TECHNIKI		Temat: Teoria błędów	Nazwisko i imię Josiek		Ocena:
ZAKŁAD FIZYKI

1. Pomiary Fizyczne

Istotą pomiaru fizycznego jest porównanie wielkości mierzonej z ustalonym wzorcem, czyli jednostką - liczbowe ujęcie tej wielkości w ustalonych jednostkach. Wielkości występujące w doświadczeniach mogą być dostępne pomiarom bezpośrednim, np.: pomiar masy ciała za pomocą wagi, jak i pośrednim, np.: badanie przyśpieszenia ziemskiego za pomocą wahadła . w większości pomiarów fizycznych mamy do czynienia z trzema następującymi po sobie operacjami: 1. ustawienie przyrządów, 2. obserwacja zjawiska, 3. odczyt mierzonych wielkości.

2. Źródła błędów

Błędy występujące przy pomiarach fizycznych dzielimy na trzy grupy: błędy systematyczne, błędy przypadkowe i błędy grube.

a) błędy systematyczne - wynikające z niedokładności przyrządów, z błędnej metody pomiaru lub z działania czynników zewnętrznych. oczywistą jest rzeczą, że wyniki otrzymane z takich pomiarów będą częściej przesunięte w jedną lub drugą stronę, będą albo za małe, albo za duże. Poznanie błędu systematycznego pozwala na wprowadzenie do końcowych wyników stałej poprawki, która ten błąd skompresuje.

b)błędy grube - powstają w skutek fałszywego odczytania przyrządów lub nieprawidłowego zapisania. Jaskrawym przykładem takiego typu błędu jest np.: zapisanie odczytań długości w centymetrach a nie w milimetrach. Błędy grube przewyższają zwykle kilkakrotnie błędy reszty pomiarów i można je dzięki temu łatwo zauważyć. przyjęto odrzucać wyniki obarczone grubymi błędami i jeśli to możliwe, powtarzać pomiary.

c) błędy przypadkowe - występowanie tego rodzaju błędów nie jest zjawiskiem chaotycznym, lecz podlega pewnej prawidłowości, której matematyczne sformułowanie stanowi zagadnienie węzłowe teorii błędów.

Do przypadkowych wydarzeń statystycznych, jakimi są pojawiające się przypadkowo błędy pomiarów, stosuje się teorię prawdopodobieństwa. Matematycznie określamy ją jako stosunek liczby n danych przypadków do ogólnej liczby zachodzących wydarzeń N.

Nie wszystkie błędy są jednakowo prawdopodobne: błędy małe pojawiają się w większej liczbie, błędy duże pojawiają się rzadziej. Na drodze matematycznych rozważań można znaleźć zależność prawdopodobieństwa występowania błędu od jego wartości, którą oznaczamy przez x.

Zależność tą przedstawia równanie:

gdzie x jest wartością błędu, y(x)-częstotliwością błędu, h - liczbą stałą.

Równanie to, zwane PRAWEM GAUSSA, jest podstawowym prawem teorii błędów.

Występująca w równaniu Gaussa stała doświadczalna h decyduje o tym czy krzywa jest więcej czy mniej stroma. Jest ona tym większa im dokładniejszy jest przyrząd.

3. Rodzaje błędów

Wszystkie przybliżone wartości wielkości fizycznych obarczone są pewnym błędem, który określamy jako:

a) błąd bezwzględny, albo absolutny

b) błąd względny

ad. a) Błędem bezwzględnym nazywamy różnicę między dokładną wartością rzeczywistą a jej wartością przybliżoną, czyli:

gdzie
jest to bezwzględny błąd pomiaru, X - prawdziwa dokładna wartość mierzonej wielkości, A - wartość przybliżona otrzymana z pomiaru.

Błędy bezwzględne są wartościami mianowanymi, tak jak i wielkości, do których się odnoszą.

ad. b) Błędem względnym danej wielkości nazywamy stosunek błędu bezwzględnego do dokładnej wartości mierzonej wielkości.

gdzie:

δ błąd względny

Wielkość „X” w powyższych jest nam nie znana; stąd wniosek, że dokładnej wartości , jak i δ określić nie możemy. Jednak, jeżeli założymy, że błąd bezwzględny  jest wielkością małą w porównaniu z „X” czy „A”, czyli

<<X i δ<<A

To można przyjąć, że obie wielkości „X” i „A” są bardzo zbliżone i we wzorze na błąd względny możemy zastąpić „X” wielkością „A” stąd wzór przyjmie postać

przy powyższych założeniach

δ 

Błąd względny wyrażamy w procentach, więc

δ=100 x δ%

Przekształcając powyższy wzór otrzymujemy wartość błędu bezwzględnego

   x δ

Chociaż doprowadziliśmy do wyeliminowania nieznanej wartości „X” , nadal pozostała nieznana wartość  tj. dokładna wartość błędu bezwzględnego.

Z konieczności musimy przyjąć wartość przybliżoną błędu bezwzględnego. Przy dokładnie wykonywanych pomiarach błędy bezwzględne nie powinny przekraczać tzw. Dokładności pomiarów, to jest najmniejszej wielkości jaką możemy odczytać posługując się danym przyrządem. Przykładowo pomiar śruba mikrometryczną można wykonać z dokładnością do 0,01mm, więc

  ,mm

Błędy względne są wielkościami niemianowanymi. Dzięki temu można porównać dokładności pomiarów wielkości różnorodnych, np. pomiary mas, czasu, długości.

4. Znak błędów wielkości przybliżonych

Dokonując pomiarów nigdy nie możemy określić czy popełniamy błąd w kierunku powiększenia mierzonej wielkości „-”, czy też w kierunku jej zmniejszenia „+”. Zatem błędy wartości przybliżonych są albo dodatnie albo ujemne.

W następstwie tej okoliczności otrzymujemy wzory :

X=A ± 



δ ±

A

  ±  x δ

Dla przybliżonych wartości stałych takich jak: e, , itp. możemy określić nie tylko przybliżoną wartość błędów bezwzględnych ale i ich znak, gdyż zawsze wiemy, czy są one wzięte z tablic z nadmiarem czy też z niedomiarem.

5. Postulat średniej arytmetycznej pomiarów.

Przy pomiarach jednakowej dokładności najbardziej prawdopodobną, najlepszą wartością mierzonej wielkości okazuje się średnia arytmetyczna otrzymanych wyników pomiarów.

Jest ona określana wyrażeniem:

6. Wskaźniki dokładności dla pojedynczych pomiarów.

1. błąd średni kwadratowy

2. błąd prawdopodobny

3. błąd przeciętny

ad. a) Błąd średni kwadratowy określa się przez szukanie tej miary współczynnika h, przy którym równoczesne pojawienie się błędów
,
,...,
, jest najbardziej prawdopodobne.

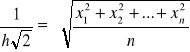
Prawa strona - błąd średni kwadratowy.

ad. b) Błąd prawdopodobny - ma taką wartość, że prawdopodobieństwo błędu większego lub mniejszego od niego jest równa połowie. Na podstawie rachunku opartego na krzywej Gaussa otrzymujemy:

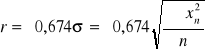
ad. c) błąd przeciętny
definiujemy jako średnią arytmetyczną wszystkich błędów indywidualnych.

7. Metoda różniczki zupełnej

Jeśli przyjąć, że szukana wielkość jest funkcją kilku zmiennych:

y = f(x₁ , x₂ , . . . , x_n)

to różniczka zupełna przyjmuje postać:

Po zastąpieniu różniczek przyrostami skończonymi otrzymamy:

Przyrostom skończonym można przypisać sens fizyczny błędów (systematycznych, maksymalnych). Uwzględniając regułę dodawania błędów otrzymamy ostatecznie:

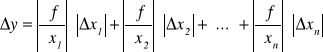
lub inaczej

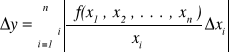
Jeśli poszczególne wielkości wchodzące do naszej złożonej funkcji mierzymy wielokrotnie a następnie obliczamy odchylenia standardowe średniej, to wyrażenie na odchylenie standardowe średniej arytmetycznej wielkości złożonej przyjmuje postać:

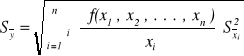
8. Metoda pochodnej logarytmicznej

Jeżeli analizowane złożone wyrażenie jest iloczynem dowolnych potęg wielkości prostych,

to po zlogarytmowaniu otrzymamy:

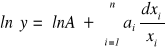
Różniczkując równanie otrzymujemy:

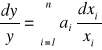
Jeśli poszczególne różniczki występujące w powyższym wyrażeniu potraktujemy jako błędy maksymalne i uwzględnimy najbardziej niekorzystną sytuację oraz zsumujemy błędy biorąc ich bezwzględne wartości, to błąd względny wyznaczania wielkości złożonej można wyliczyć za pomocą następującej zależności:

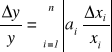
Jeśli poszczególne wielkości proste mierzyliśmy wielokrotnie i obliczaliśmy odchylenia standartowe wartości średnich, to błąd względny w takim przypadku należy obliczyć wg wzoru:

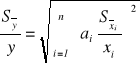
9. Graficzna analiza błędów

Prezentacja błędów pomiarowych na wykresie polega na wykreśleniu prostokąta błędu z środkiem w punkcie pomiarowym. wysokość prostokąta odpowiada 2 ⋅ ΔY, a jego szerokość 2 ⋅ ΔX, gdzie ΔX i ΔY są błędami maksymalnymi lub odchylenia standardowymi. Jeśli wartość błędu jednej wielkości jest zbyt mała by narysować prostokąt, lub też nie znamy jego wartości to ograniczamy się do narysowania słupka błędu, czyli odcinka o długości odpowiadającej podwojonemu błędowi drugiej wielkości. W skali logarytmicznej lub półlogarytmicznej na wykresach biegunowych itp. prostokąty błędów będą odpowiednio zdeformowane. Prostokąty błędów nanosimy na kilka punktów pomiarowych (skrajne i środkowe) oraz te, które odbiegają od przewidywanej krzywej.

Po otoczeniu punktów pomiarowych prostokątami błędów rysujemy linią przerywaną dwie krzywe po obu stronach wykresu, przechodzące przez narożniki prostokątów. Jest to tzw. obwiednia błędów. Założona wartość wielkości i jest obarczona błędem Δi. Rysujemy pas o szerokości odpowiadającej 2⋅Δi, który przecina obwiednię. Bierzemy najbardziej niekorzystne punkty przecięcia tych pasów i znajdujemy przedział wielkości X: X₁<X_x<X₂ . W niektórych przypadkach interesująca wielkość fizyczna jest wyznaczana jako nachylenie wykresu (np. z charakterystyk tranzystora znajdujemy jego parametry. Omawiany tutaj sposób jest zalecany wtedy, gdy interesujący nas odcinek wykresu nie jest idealną linią prostą. Skrajne punkty pomiarowe odcinka charakterystyki otaczamy prostokątami błędów. Przez te prostokąty można poprowadzić wiele prostych. Nas interesują przypadki ekstremalne. Skrajne proste przechodzą przez przeciwległe rogi prostokątów. Nachylenie charakterystyki obliczamy jako średnią arytmetyczną nachyleń skrajnych prostych:

Błąd maksymalny nachylenia oblicza się w następujący sposób:

Narzędzia pomiarowe

Suwmiarka:

-Pozwalają na mierzenie długości. Suwmiarkę stanowią dwie metalowe skale. Skala nieruchoma posiada zwykle podziałkę milimetrową. Skala ruchoma, zwana noniuszem posiada dziesięć podziałek na odcinku równym 9mm.

Nazwa przyrządu pomiarowego	Zakres pomiarowy	Dokładność przyrządu
Suwmiarka	140 200 315 400	0,1 0,05 0,02

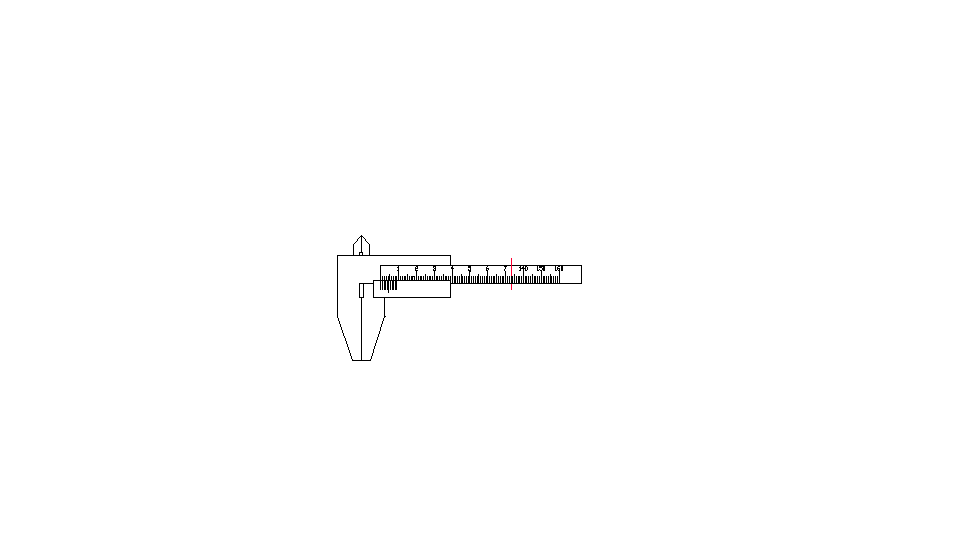
Pomiar suwmiarką - zasada noniusza

10 działek noniusza = 9 działek podziałki głównej

1 działka noniusza = 0,9 działek podziałki głównej

Każda działka noniusza jest mniejsza o 0,1 mm od działki podziałki głównej.

Szczęka nieruchoma

z podziałką główną

Noniusz

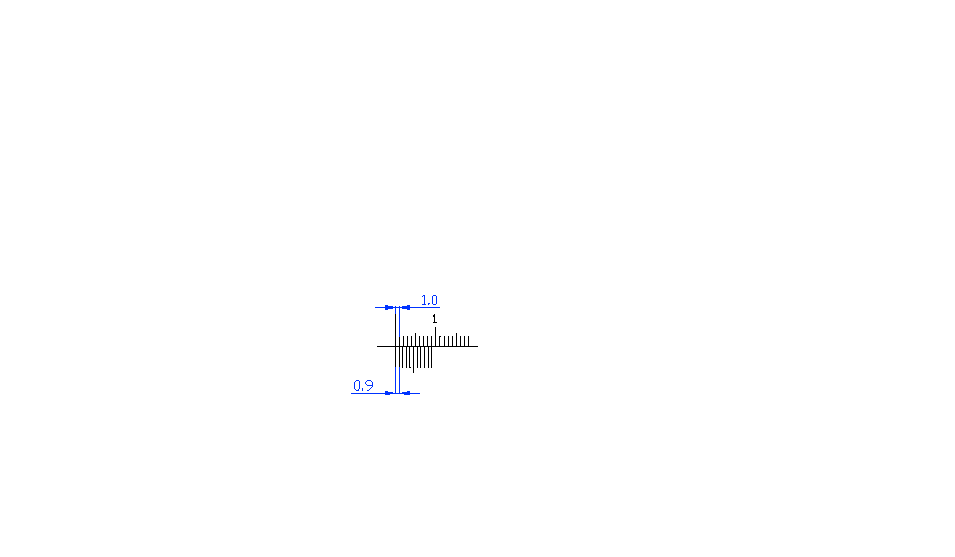
Śruba mikrometryczna

- pozwala mierzyć wymiary liniowe.

Nazwa przyrządu pomiarowego	Zakres pomiarowy	Dokładność przyrządu
Mikrometr (śruba mikronometryczna)	0-25 25-50 75-100 100-125 125-150 150-175 175-200	0,01mm

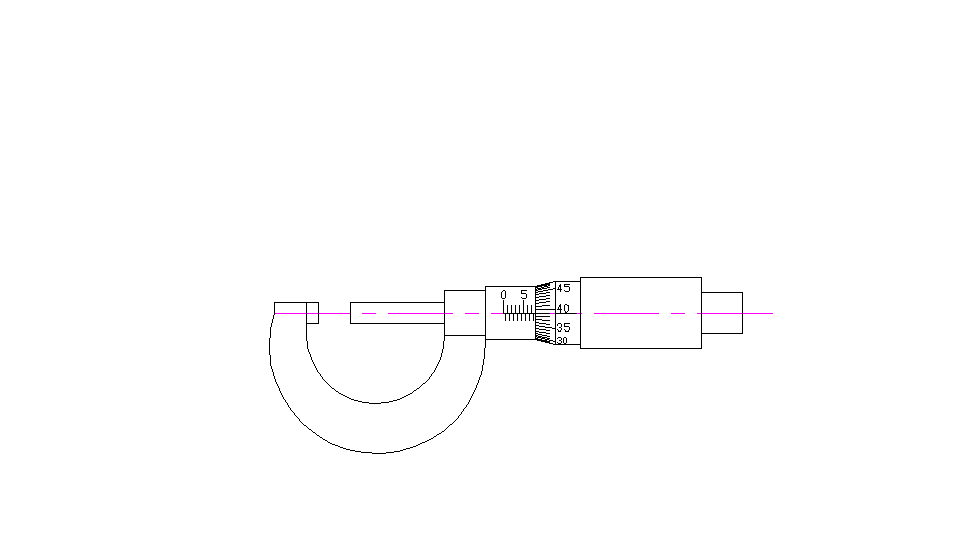
Pomiar mikrometrem

Nad kreską wskaźnikową naniesiona jest podziałka milimetrowa. Pod kreską wskaźnikową naniesione są kreski, które dzielą na połowy podziałkę milimetrową (górna).

Skok śruby mikrometrycznej równa się 0,5 mm. Pełny obrót bębna powoduje przesunięcie wrzeciona o 0,5 mm.

Obrócenie bębna o 1 działkę skali poprzecznej powoduje przesunięcie się wrzeciona o

Skok śruby 0,5

= = 0,01mm

• 50

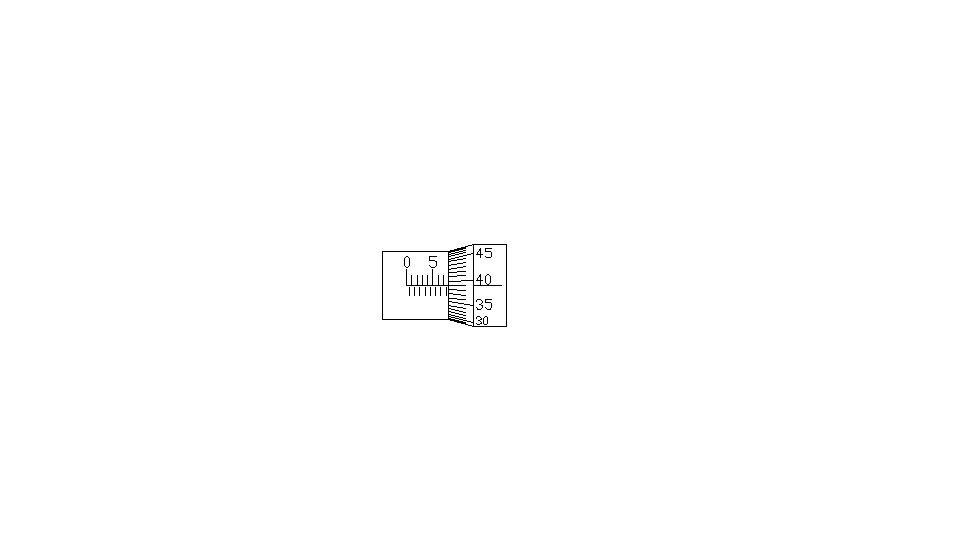
Odczyt:

1. Krawędź bębna odsłania 7,5mm

2. 39 kreska nakrywa się z kreską wskaźnikową 39 x 0,01 = 0.39

3. Odczyt całkowity 7,89mm

---