POLITECHNIKA ŚLĄSKA

WYDZIAŁ ELEKTRYCZNY

Gr.2 1997/98

SPRAWOZDANIE

TEMAT: Polaryzacja światła.

SEKCJA 5:

Pastuła Marcin

Krzyżowski Marek

1.Podstawy teoretyczne.

Polaryzacja jest zjawiskiem charakterystycznym dla fal poprzecznych i polega na uporządkowaniu kierunków drgań. Polaryzacja fal może wystąpić w wielu przypadkach, np. przy braku symetrii osiowej w źródle, podczas przechodzenia przez ośrodek anizotropowy, przy załamaniu i odbiciu dwóch ośrodków itp. W celu stwierdzenia polaryzacji należałoby zmierzyć wielkości przesunięć w różnych kierunkach prostopadłych do kierunku rozchodzenia się fali. W przypadku granicznym asymetrii kierunek tego przesunięcia leży zawsze w pewnej określonej płaszczyźnie, zaś w innych kierunkach przesunięcie to jest równe zero. Taka fala jest spolaryzowana liniowo. Źródła fal poprzecznych emitują zwykle w ośrodkach izotropowych taką falę.

Ciekawa sytuacja zachodzi w przypadku superpozycji dwóch fal spolaryzowanych liniowo i rozchodzących się w tym samym kierunku. Można wówczas wyróżnić trzy szczególne przypadki dla: fal spójnych, częściowo spójnych, niespójnych. Jeśli dwa źródła emitują fale spójne a ich wektory przesunięć są prostopadłe względem siebie, to w wyniku superpozycji otrzymamy falę spolaryzowaną eliptycznie. W przypadku fali elektromagnetycznej koniec wektora natężenia pola elektrycznego będzie zataczał elipsę z określoną częstotliwością. Jeżeli fazy obu fal składowych są takie same, to fala wypadkowa będzie spolaryzowana liniowo. Zaś w przypadku jednakowych amplitud różnicy faz spełniających warunek:

elipsa przekształca się w okrąg, a fala jest spolaryzowana kołowo.

Polaryzacja częściowa występuje, gdy tylko część źródeł wysyła fale spójne. Miarą stopnia polaryzacji jest stosunek gęstości strumienia energii składowej spolaryzowanej do gęstości strumienia całej fali. W przypadku fal niespójnych w wyniku nałożenia otrzymamy falę niespolaryzowaną. W źródłach rzeczywistych, np. żarówkach, w 1s zachodzi olbrzymia liczba emisji fal, a wszystkie efekty polaryzacyjne uśredniają się w czasie i obserwacja polaryzacji jest niemożliwa. A więc światło jest nie spolaryzowane tylko w tedy, gdy nie możemy stwierdzić, czy jest spolaryzowane, czy też nie. Jednym ze sposobów polaryzacji światła jest polaryzacja przez odbicie.

Pierwszą osobą która stwierdziła, że światło odbite od szkła jest spolaryzowane był E.L.Malus. Nieco później zostały podane wzory określające te zjawisko. Dla przypadku, gdy składowa natężenia pola elektrycznego E jest prostopadła do płaszczyzny padania, w świetle odbitym zachodzi warunek:

a dla światła załamanego:

Analogiczne związki zachodzą dla składowej równoległej:

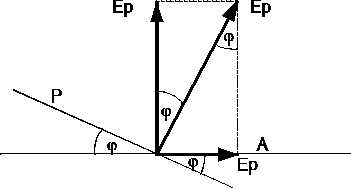
Rys.1 Składowe wektora świetlnego.

Gdy wiązka światła spolaryzowana w płaszczyźnie prostopadłej do płaszczyzny padania ulega odbiciu pod kątem α = 90⁰ - β, zwanym kątem Brewstera, to natężenie wiązki odbitej z równoległą płaszczyzną drgań staje się równe zeru:

ponieważ

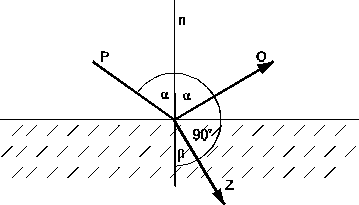
tg(α + β) = ∝

Rys.2 Polaryzacja światła przez odbicie.

W świetle odbitym pozostaje więc wiązka światła spolaryzowanego w płaszczyźnie padania. Można wykazać, że z powyższego warunku wynika:

tgα_B = n

Gdzie n - współczynnik załamania materiału. Jeśli płaszczyzna polaryzacji światła padającego tworzy kąt ϕ z płaszczyzną padania, to płaszczyzna polaryzacji ulegnie skręceniu o kąt ψ:

Drugim sposobem dwójłomność kryształów. Kryształy anizotropowe wykazują tzw. anomalne załamanie, polegające na rozdzieleniu wiązki w świetle załamanym. Jest to szczególny przypadek dwójłomności światła. Jeśli oś optyczna kryształu nie jest równoległa do powierzchni kryształu, to wiązka spolaryzowana w płaszczyźnie prostopadłej do płaszczyzny padania przechodzi przez kryształ nie ulegając załamaniu. Jest to tzw. promień zwyczajny. Dla drugiej płaszczyzny polaryzacji wystąpi zjawisko załamania światła, a promień nazywamy nadzwyczajnym. Jeśli będziemy obracać płytkę wokół kierunku padającej wiązki, to na ekranie zobaczymy plamkę promieniowania nadzwyczajnego obracającą się wokół plamki promieniowania zwyczajnego. Zjawisko dwójłomności wskazuje na różne wartości światła dla różnych płaszczyzn polaryzacji w stosunku do osi optycznej.

Z bardziej złożonymi zjawiskami dwójłomności mamy do czynienia w przypadku przejścia światła przez kryształy dwuosiowe. Do grupy takich kryształów należą kryształy trójskośne, jednoskośne i rombowe. W takich kryształach w świetle załamanym mamy dwa promienie nadzwyczajne spolaryzowane w płaszczyźnie padania oraz w płaszczyźnie do niej prostopadłej.

Dwójłomność wymuszona to kolejny sposób polaryzacji światła. Można ją wywołać w przezroczystych cieczach izotropowych poprzez wytworzenie w nich naprężeń albo wprowadzając je do pola elektrycznego lub magnetycznego. Pierwsza z metod może być wykorzystywana do wizualizacji naprężeń w modelach części maszyn. Różnica współczynników załamania promieni zwyczajnego i nadzwyczajnego zależy od naprężenia p w materiale:

gdzie λ - długość fali, k - stała materiałowa.

Zjawisko dwójłomności można również wywołać umieszczając ciecze organiczne w poprzecznym polu magnetycznym.

Przytoczone przykłady nie wyczerpują wszystkich możliwych sposobów otrzymania światła spolaryzowanego. Wspomnijmy jeszcze o selektywnym pochłanianiu, obiciu od powierzchni metalicznych, polaryzacji przy całkowitym wewnętrznym odbici, polaryzacji chromatycznej itp.

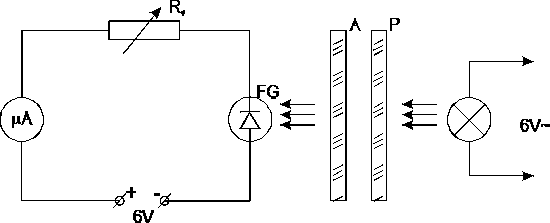
2.Układ pomiarowy.

Rys.3 Schemat obwodu do sprawdzania prawa Malusa.

Rys.4 Schemat obwodu zasilania solenoidu.

3.Przebieg ćwiczenia.

Ćwiczenie to składało się z dwóch części. W pierwszej z nich sprawdzaliśmy prawo Malusa. Należało:

1. Połączyć obwód według schematu pokazanego na rys.3.

2. Ustalić taką wartość oporu R_d, aby przy kącie ϕ = 0⁰ wychylenie miernika nie przekraczało zakresu pomiarowego.

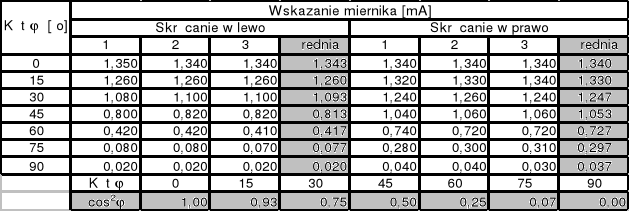
3. Zmieniając kąt skręcania filtrów polaryzacyjnych w przedziale -90⁰ ± +90⁰ co 15⁰ notujemy wskazania miliamperomierza.

4. Dla każdego kąta notujemy po 3 pomiary.

5. Rysujemy wykres (we współrzędnych biegunowych) zależności wskazań miernika od kąta skręcenia filtrów polaryzacyjnych.

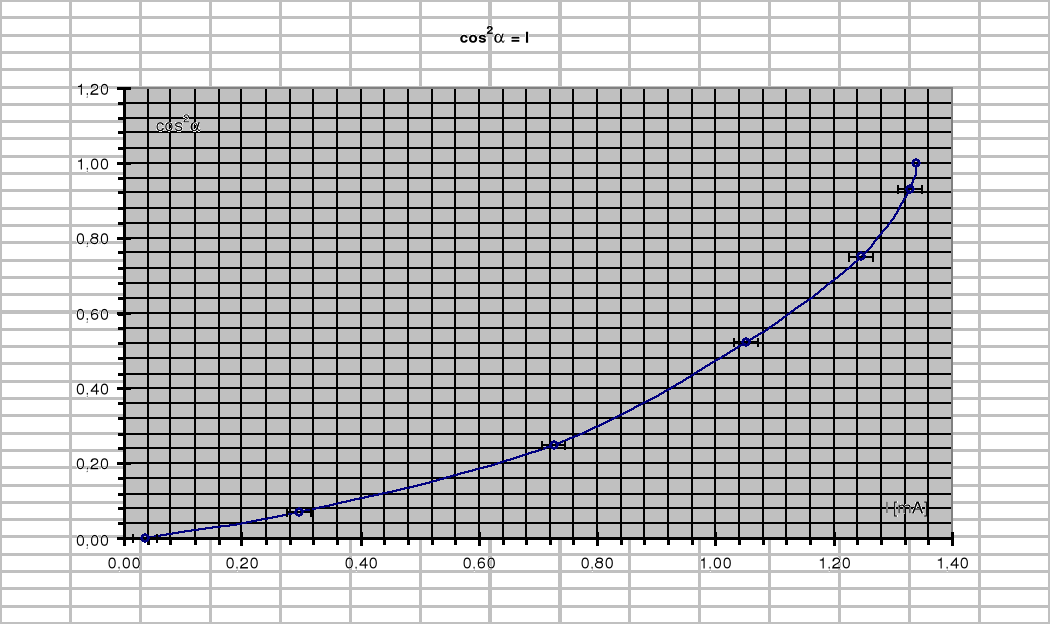
6. Rysujemy wykres zależności wskazań miernika od cos²ϕ.

7. Przeprowadzamy graficzną analizę błędów.

W drugiej części zatytułowanej „Wyznaczanie stałej Verdeta” należało:

1. Połączyć cewkę jak na rys.4.

2. Zmieniając natężenie prądu płynącego przez cewkę w zakresie od 14 [A] do 0 co 1 [A] mierzymy (trzykrotnie) kąt skręcenia płaszczyzny polaryzacji.

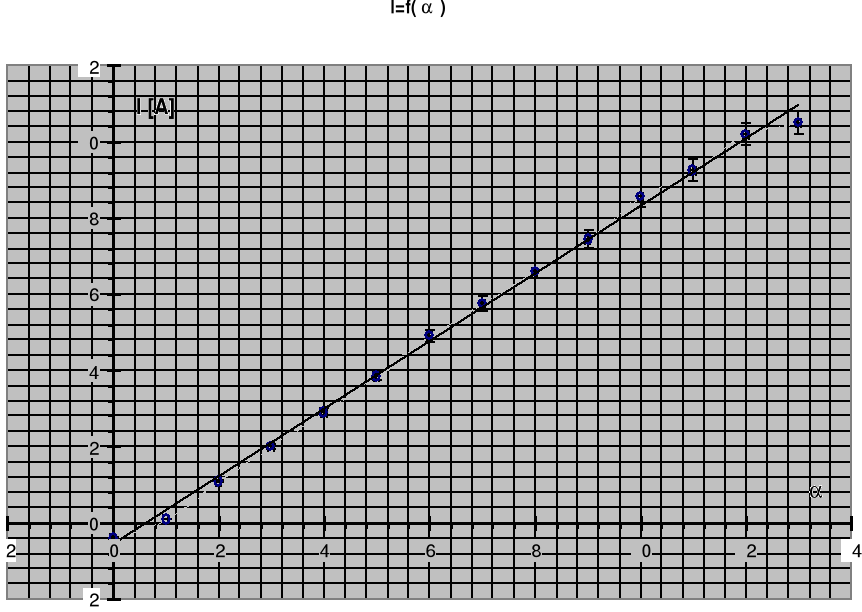
3. Rysujemy wykres zależności kąta skręcenia płaszczyzny polaryzacji od natężenia prądu

α =k∗I

gdzie l = 20 cm -długość kuwety, a

k = μ₀ωbnl

jest współczynnikiem proporcjonalności obliczonym metodą regresji liniowej

4. Metodą regresji liniowej obliczamy współczynnik k a następnie stałą Verdeta:

5. Przeprowadzamy rachunek błędów.

4.Obliczenia.

PAWO MALUSA

STAŁA VERDETA:

Metodą regresji liniowej obliczamy współczynnik proporcjonalności:

k = (8,82 ± 0,16)∗10^-1 a następnie podstawiamy k do wzoru na stałą Verdeta:

gdzie:

l = 20 [cm] = 0.2 [m] - długość kuwety,

n = 60 [m^-1] - liczba zwojów na jednostkę długości cewki,

b = 116 - stała aparaturowa,

μ₀ = 4∗Π∗10^-7 [H/m] - przenikalność magnetyczna próżni.

Jak podstawimy te wartości do wzoru na stałą Verdeta to trzymamy:

ω = 514,219 [st/T⋅m]

Metodą pochodnej logarytmicznej obliczamy błąd stałej:

w efekcie otrzymujemy wynik:

ω = (514,3 ± 9,1) [ts/Tm],

Wartość ta jest zbliżona do wartości tablicowej, której wartość dla jodku potasu wynosi:

ω = 568,3 [st/Tm].

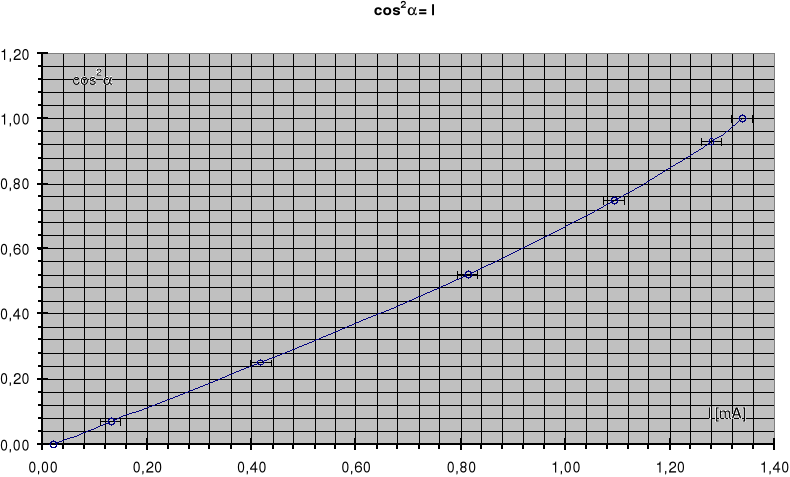
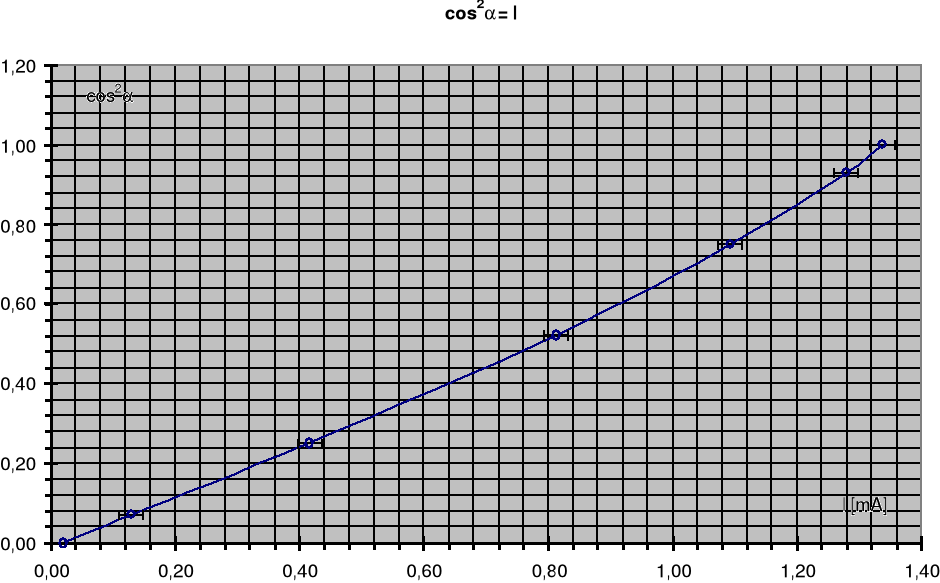
5.Wykresy.

Wyk.1 Zależność cos² od prądu I przy skręcie w lewo.

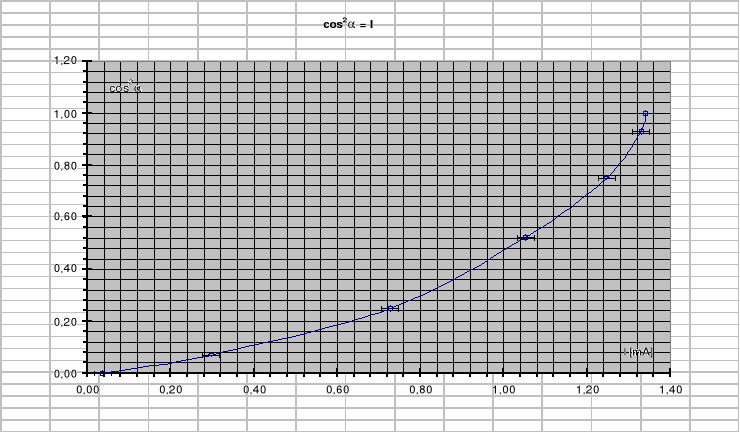
Wyk.2 Zależność cos² od prądu I przy sręcie w prawwo.

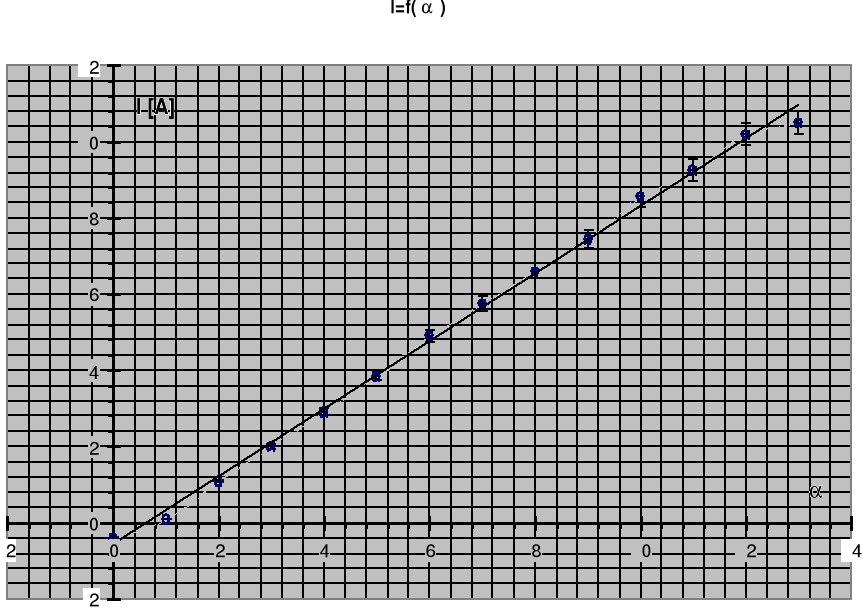
Wyk.3 Zleżność kąta skręcania płaszczyzny polaryzacji od natężenia prądu.

1

1

---