Nieliniowe modele ekonometryczne

W ekonometrii często wykorzystujemy modele liniowe gdyż:

• mają prostą interpretację ekonomiczną

• są łatwe w estymacji

• łatwa jest ich statystyczna weryfikacja

• często są wystarczająco dobrym przybliżeniem rzeczywistości ekonomicznej

• wiele modeli nieliniowych daje się sprowadzić do postaci liniowej (linearyzować).

Najprostszym przykładem jest model liniowy jednorównaniowy:

Y = a₀ + a₁X₁ + a₂X₂ + … + a_nX_n +  (1)

gdzie: Y - zmienna objaśniania,

X­_i ­- zmienne objaśniające, i = 1, 2, … n

a_i - nieznane parametry strukturalne modelu, i = 0, 1, … n

 - składnik losowy.

Naszym celem jest oszacowanie parametrów modelu a_i , i = 0, 1, … n.

W równaniu (1) zarówno zmienne objaśniające X­_i ­jak i parametry strukturalne a_i , pojawiają się w sposób liniowy. Jeśli model opisujący zależność między zmienną objaśnianą i zmiennymi objaśniającymi nie jest postaci (1), to jest to model nieliniowy, trudniejszy do analizy. Ponieważ jednak naszym celem jest oszacowanie parametrów strukturalnych, więc uznamy, ze model jest prosty jeśli będzie liniowy ze względu na parametry (nie musi być liniowy ze względu na zmienne). W dalszych rozważaniach będziemy klasyfikowali modele na liniowe ze względu na parametry strukturalne i nieliniowe ze względu na te parametry.

Przykład 1.

1. Y = a + bX + cZ +  ; model liniowy ze względu na parametry i zmienne,

2. Y = a + bX + cX² +  ; model liniowy ze względu na parametry i nieliniowy ze względu na zmienne,

3. Y = a + bX + b²Z +  ; model nieliniowy ze względu na parametry i liniowy ze względu na zmienne,

4. Y² = a + bX + b²X² +  ; model nieliniowy ze względu na parametry i zmienne.

Ogólna postać modelu liniowego ze względu na parametry ma postać:

g(Y) = a₀ + a₁f₁(X) + a₂f₂(X) + … + a_nf_n(X) +  (2)

gdzie: Y - zmienna objaśniania,

X = (X­₁, X­₂,… X­_n) ­- wektor zmiennych objaśniających

a_i - nieznane parametry strukturalne modelu, i = 0, 1, … n

 - składnik losowy.

Jeśli g(Y) = Y, to mówimy, że (2) jest modelem bezpośrednio liniowym. Jeśli g jest funkcja odwracalną to (2) jest linearyzcją (sprowadzeniem do postaci liniowej) modelu (2a).

Y = g^-1{a₀ + a₁f₁(X) + a₂f₂(X) + … + a_nf_n(X) +  (2a)

Model (2a) nazwiemy modelem linearyzowanym.

Przykład 2.

Badamy model (wykładniczo hiperboliczny) postaci:

; gdzie d, h > 0 (3a)

Model (3a) jest modelem linearyzowalnym. Logarytmując obustronnie równanie (3a) przechodzimy do modelu (3b) postaci:

ln (Y) = ln(d) + b/X + ln(h) (3b)

Przyjmując oznaczenia: a = ln(d),  = ln(h) sprowadzamy równanie (3b) do postaci liniowej ze względu na parametry:

ln(Y) = a + b/X +  (

Używając metody wyznaczania parametrów w modelu liniowym, możemy obliczyć â estymator parametru a. Powstaje jednak pytanie czy exp(â) jest dobrym estymatorem parametru d. Przy odpowiednich założeniach (klasycznych założeniach stochastycznych) exp(â) jest zgodnym estymatorem parametru d. Jest to jednak estymator obciążony.

Jak widać na podstawie przykładu 2, możemy wyznaczać parametry strukturalne modelu linearyzowanego. Podobnie możemy postępować w ogólnym przypadku równania (2). Zagadnienie wyznaczania oryginalnych parametrów modelu przed linearyzacją, na podstawie estymatorów a_i parametrów modelu linearyzowanego, nazywamy zagadnieniem identyfikacji parametrów oryginalnych.

Model liniowy czy nieliniowy? Jaki model powinniśmy zastosować dla opisu badanego zjawiska, zbioru zaobserwowanych danych? Nie istnieją jednolite reguły postępowania. Musimy posłużyć naszą wiedzą ekonomiczną, doświadczeniem związanym z budową modeli ekonometrycznych, testami statystycznymi.

Przyrost krańcowy i elastyczność.

Przyrost krańcowy zmiennej objaśnianej Y względem zmiennej objaśniającej X_i to pochodna cząstkowa:

Przyrost krańcowy interpretujemy jako proporcję: przyrostu wielkości Y do przyrostu wielkości X_i, przy małym przyroście X_i i niezmienionych pozostałych wielkościach zmiennych objaśnianych. W przypadku, gdy przyrost krańcowy jest stałą niezależną od wszystkich zmiennych objaśniających to zmienna X_i w modelu pojawia się w sposób liniowy, zaś współczynnik przy X_i jest równy przyrostowi krańcowemu. Jeśli przyrost krańcowy nie jest wielkością stałą, to X_i w modelu występuje w sposób nieliniowy.

Elastyczność cząstkowa jest również miarą określającą zmienność zmiennej objaśnianej w zależności od zmienności zmiennej objaśniającej X_i. Elastyczność to iloczyn przyrostu krańcowego i proporcji X_i do Y:

W modelu liniowym E_Y|Xi = a_i · (X_i / Y).

Przykład 3

Model potęgowy: Y = a · X^b · 

Linearyzujemy logarytmując obie strony równania:

ln(Y) = ln(a) + b·ln(X) + ln()

Przyrost krańcowy dla modelu potęgowego wynosi: a · b · X^b-1 · 

Elastyczność Y względem X wynosi: b

Przykład 4

Rozważmy model postaci: Y = a + b·ln(X) +  , przy założeniu , że X>0.

Przyrost krańcowy Y względem X: dY/dX = b/X

Obliczmy elastyczność Y względem X:

dY/dX · X/Y = b/X · X/Y = b/Y

Przykład A

Na podstawie naszej wiedzy o badanych zależnościach wiemy, że przyrosty zmiennej objaśnianej Y względem zmiennych objaśnianych X₁, X₂, … X_n są stałe. Stałe przyrosty sugerują liniową postać modelu:

Y = a₀ + a₁X₁ + a₂X₂ + … + a_nX_n + 

Przykład B

Na podstawie naszej wiedzy o badanych zależnościach wiemy, że przyrosty krańcowe zmiennej objaśnianej Y względem zmiennych objaśnianych X₁, X₂, … X_n są stałe. Stałe przyrosty krańcowe sugerują liniową postać modelu:

Y = a₀ + a₁X₁ + a₂X₂ + … + a_nX_n + 

Przykład C

Na podstawie naszej wiedzy o badanych zależnościach wiemy, że elastyczności zmiennej objaśnianej Y względem zmiennych objaśnianych X₁, X₂, … X_n są stałe. Stałe elastyczności sugerują potęgową postać modelu:

Y = a₀ · X₁^a1 · X₂^a2 ·…· X_n^an · 

Zadanie (Nowak, 4.1)

Zaproponować postać analityczną modelu ekonometrycznego opisującego wartość produkcji P przedsiębiorstwa od mocy zainstalowanych maszyn M, zatrudnienia robotników Z oraz zużycia surowca S, jeśli wiadomo, że elastyczność produkcji względem zmiennych M, Z i S są stałe.

Rozwiązanie

P = a₀ · M^a1 · Z^a2 · S^a3 · 

Zadanie (Nowak, 4.3)

Zaproponować postać analityczną modelu ekonometrycznego opisującego zależność poziomu produkcji Y przedsiębiorstwa od wartości trwałego majątku produkcyjnego X₁ i zatrudnienia robotników produkcyjnych X₂ przy założeniu, krańcowe wartości majątku trwałego i zatrudnienia są stałe.

Rozwiązanie

Y = a₀ + a₁ X₁ + a₂ X₂ + 

Wybór postaci analitycznej modelu na podstawie wykresu rozrzutu punktów z próby

Metoda stosowana głównie dla modeli z jedną zmienną objaśniającą: Y = f(X,). Wykonujemy wykres rozrzutu punktów z próby (x₁, y₁), (x₂, y₂), … , (x_m, y_m). Wzrokowo staramy się ocenić wzdłuż wykresu jakiej znanej nam funkcji układają się te punkty.

(rysunek)

Typowe modele liniowe ze względu na parametry - przykłady

W modelach liniowych ze względy na parametry, szacowanie parametrów weryfikacja modeli i prognozowanie dokonywana jest tak jak w modelach liniowych przy odpowiednim przedefiniowaniu zmiennych. Zmienne przedefiniowane nazywamy zmiennymi pomocniczymi.

Model wielomianowy

Zmienna Y objaśniana jest za pomocą wyrażenia wielomianowego względem zmiennej X. W praktyce n=1,2,3. Dla n=2 model funkcji kwadratowej:

Y = a₀ + a₁X + a₂X² (4)

Równanie (4) może reprezentować funkcję przeciętnego kosztu w zależności od X wielkości produkcji. W tym wypadku zakładamy, że: a₀ > 0, a₂ > 0.

Model logarytmiczny (półlogarytmiczny): Y = a₀ + a₁ln(X) + a₂ln(Z) + 

Model hiperboliczny: Y = a₀ + a₁/X + a₂*Z + 

Modele logarytmiczny i hiperboliczny, są wykorzystywane w analizie konsumpcji jako modele o wykresach będących krzywymi Engla, gdzie Y to konsumpcja, X - dochód, Z - inny parametr.

Model z interakcjami: Y = a₀ + a₁·X + a₂·Z + a₃·X·Z + 

Ogólnie modele z interakcjami uwzględniają to, że wpływ zmiany jednej zmiennej objaśniającej zależy od wartości przyjmowanej przez inne zmienne objaśniające. Uwzględnienie w modelu iloczynu zmiennych objaśniających jest jednym z najprostszych modelu tego typu.

Pochodna cząstkowa Y po X: dY/dX = a₁ + a₃·Z , czyli jest liniową funkcją Z. Jeśli Z będzie interpretowane jako czas Z = t, to krańcowy przyrost M_Y|X = a₁ + a₃·t, będzie liniową funkcją czasu.

Modele linearyzowalne ze względu na parametry strukturalne:

Model potęgowy (podwójnie logarytmiczny, logarytmiczno-liniowy).

Y = a · X^b · Z^c · exp() lub ln(Y) = ln(a) + b*ln(X) + c*ln(Z) + 

Jest to jeden z bardziej popularnych w ekonometrii modeli nieliniowych. Stosowany jest między innymi jako ekonometryczna funkcja produkcji Cobba-Douglasa lub jako ekonometryczna funkcja popytu.

Model wykładniczy (półlogarytmiczny)

Y = exp(a + b·X + ) lub ln(Y) = a + b·X + 

Model wykładniczy stosuje się zwykle do ilustracji wykładniczego wzrostu zmiennej Y względem zmiennej X.

Model S-krzywej (wykładniczo-hiperboliczny)

Y = exp(a + b/X + ) lub ln(Y) = a + b/X + 

Jeśli X jest interpretowane jako czas X=t, to model stosuje się jako model trendu o wykresie zbliżonym do krzywej logistycznej.

Składniki losowe i estymacja modelu

Modele liniowe względem parametrów szacujemy klasyczną metodą najmniejszych kwadratów (KMNK). Jeżeli model podlegał linearyzacji, to przekształceniu podlega również losowe zaburzenie. Możemy stosować metodę najmniejszych kwadratów jeśli przekształcone zaburzenie losowe spełnia wymagania KMNK.

Np. badając model: Y = exp(b·X) · ,

sprowadzamy go do postaci liniowej przekształceniem logarytmicznym: ln(Y) = b*X +ln()

Założenia KMNK wymagają by zmienna ln() miała rozkład normalny o wartości oczekiwanej zero. Oznacza to, że sama zmienna losowa  ma rozkład logarytmiczno-normalny i że w modelu jest zaburzeniem multyplikatywnym, a nie addytywnym.

Funkcja logistyczna i model logitowy

Klasyczna postać modelu krzywej logistycznej to:

; gdzie a>0, b>1, g>0.

Funkcja logistyczna ma następujące własności:

1. 
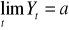
   , czyli a - to parametr określający poziom nasycenia, maksymalny poziom wartości Y

2. dla t = 0 zachodzi
   

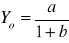
3. Y_t ma punkt przegięcia dla t = ln(b)/g

Funkcja logistyczna ma zastosowanie przy modelowaniu długookresowego wzrostu liczby ludności, reprezentacji wielkości sprzedaży nowego produktu na rynku. Popularność modelu logistycznego zaowocowała powstaniem specyficznych metod estymacji parametrów modelu. Funkcja logistyczna ma zastosowanie przy modelowaniu zmiennych jakościowych tj. przyjmujących wartości z przedziału [0,1]. Jeden z możliwych modeli dla tego typu zmiennej ma postać:

ta postać to pewien typ funkcji logistycznej. Na przykład P może oznaczać procent gospodarstw domowych posiadających jakieś dobro w danej grupie dochodowej, zaś zmienna X to średnia dochodu w dane grupie dochodowej. Ten model wygodnie jest linearyzować przez posługiwanie się zmienną: ln(P/(1-P))

zachodzi bowiem ln( P / (1-P) ) = a + b·X +  oraz należy ona do całego przedziału (-∞, +∞).

Model ten nazywa się modelem logitowym. Logitem nazywa się wielkość ln( P / (1-P) ).

X nazywa się wielkością objaśniającą logit.

Funkcje Törnquista

Funkcje Törnquista należą do rodziny funkcji o wykresie należącej do rodziny krzywych Engla. Przedstawiają wydatki w funkcji dochodów konsumenta. Wyróżniamy cztery typy funkcji Törnquista w zależności od rodzaju potrzeb zaspokajanych konsumpcją określonych dóbr.

1. 
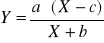
   ; a>0; c>0; b<-c; 0<X≤c lub X>-b;

dobra i usługi niższego rzędu.

2. 
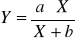
   ; a>0; b>0; X>0;

dobra podstawowe (pierwszej potrzeby.

3. 
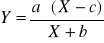
   ; a>0; b>0; c>0; X≥c ;

dobra wyższego rzędu (dalszej potrzeby).

4. 
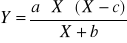
   ; a>0; b>0; c>0; X≥c ;

dobra i usługi luksusowe.

Modele segmentowe

Jeżeli w analizie szeregów czasowych możemy wyodrębnić podokresy, w których zbiory obserwacji łatwo opisują się różnymi modelami ekonometrycznymi, to tworzymy model segmentowy, inny model (segment) na każdym podokresie. Element szeregu czasowego kończący jeden segment i jednocześnie zaczynający następny nazywamy punktem zwrotnym.

Najprostszym przypadkiem jest model kawałkami liniowy, każdy segment to model trendu liniowego.

Przykład 5

Dane tworzą szereg czasowy: Y₁, Y₂,…Y_n. Rozpoznajemy (np. obserwując wykres szeregu czasowego) dwa punkty zwrotne t₁ , t₂ . Na trzech przedziałach czasowych budujemy trzy segmenty trendu liniowego:

Y_t = a₀ + a₁·t +  ; dla t < t₁ ,

Y_t = b₀ + b₁·t +  ; dla t₁ ≤ t < t₂ ,

Y_t = c₀ + c₁·t +  ; dla t₂ ≤ t ,

Funkcja produkcji

Funkcja produkcji wyraża zależność jaka zachodzi między wielkością wytworzonego produktu Y, a czynnikami mającymi wpływ na produkcję X₁, X₂,…X_n oraz zaburzeniem losowym .

Y = f(X₁, X₂,…X_n, )

W dalszych rozważaniach ograniczymy się do dwóch czynników: L - nakładów pracy oraz K - kapitału.

Własności funkcji produkcji

Funkcja produkcji zwykle jest funkcją nieliniową. W dalszym opisie dla uproszczenia opisu pominiemy zaburzenie losowe  oraz przyjmiemy zależność:

Y = f(K,L), gdzie Y>0, K>0, L>0.

Wykres funkcji produkcji tworzy powierzchnię w R³, a dokładnie mówiąc w dodatniej oktancie R³. Może na powierzchni wykresu rozpatrywać warstwice, dla każdej ustalonej wielkości produkcji Y=Y₀. Te linie warstwic będziemy nazywać liniami stałej produkcji (izokwantami produkcji).

Równanie izokwanty ma postać: f(K,L) = Y₀.

W dalszych rozważaniach zakładamy, że funkcja produkcji jest odpowiednio gładka, a mianowicie, że jest dwukrotnie różniczkowalna oraz, że wykres izokwanty jest wypukły (tak, jak wypukły jest wykres funkcji -x²). Wypukłość izokwanty oznacza, że jeśli (K₁,L₁) oraz (K₂,L₂) dają taką samą wielkość produkcji:

czyli f(K₁,L₁) = f(K₂,L₂) = Y₀ oraz 0<a<1

to a·f(K₁,L₁) + (1-a)·f(K₂,L₂) = Y₀ ≤ f(aK₁+(1-a)K₂ , aK₁+(1-a)K₂ )

Założenia, które powinna spełniać funkcja produkcji:

1. Produkcyjność krańcowa czynnika produkcji jest dodatnia, czyli pochodne cząstkowe spełniają: f_K>0, f_L>0.

Warunek 1. oznacza, że nakłady produkcyjne są efektywne, zwiększenie danego czynnika powoduje wzrost produkcji.

2. Produkcyjność krańcowa jest malejąca względem nakładów danego czynnika, czyli pochodne cząstkowe spełniają: f_KK<0, f_LL<0.

Warunek 2. oznacza, że krańcowe przyrosty maleją w miarę wzrostu danego nakładu, przy nie zmieniającym się drugim nakładzie.

3. Krańcowa produkcyjność jednego czynnika wzrasta przy wzroście drugiego czynnika, czyli pochodne mieszane f_KL = f_LK > 0.

Warunek 3. oznacza, że krańcowe przyrosty rosną przy wzroście obu nakładów.

4. Funkcja f jest jednorodna, czyli: f(aK,al.) = a^r·f(K,L), dla a>0.

Jednorodność funkcji produkcji oznacza można określi, jak zareaguje produkcja na zwiększenie wielkości nakładów. Dla r=1 jest to wzrost proporcjonalny. Dla r>1, jest rosnąca skala produkcji. Dla r<1, malejąca skala produkcji.

5. Czynniki produkcji są wzajemnie zastępowalne (zachodzi substytucja czynników produkcji).

Miarą stopnia substytucji jest krańcowa stopa substytucji czyli pochodna dK/dL lub pochodna dL/dK. Zakładamy, że te wielkości są ujemne.

Jako krańcową stopę wzajemnej substytucji (KSS) między K i L określamy współczynnik nachylenia izokwanty względem osi L:

KSS = dK/dL = -( f_L/f_K )

Współczynnik nachylenia izokwanty względem osi K wynosi:

1/KSS = dL/dK = -( f_K/f_L)

Na podstawie KSS możemy określi o ile powinien się zmienić nakład jednego czynnika, gdy drugi ulegnie zmianie o małą wielkość tak, by produkcję utrzymać na tym samym poziomie.

Jeśli KSS = -0,2 to przy spadku (L) nakładu pracy o jednostkę, należy zwiększyć nakład (K) kapitału o 0,2 jednostki, zaś przy spadku (K) nakładu kapitału o jednostkę, należy zwiększyć nakład (L) pracy o 5 jednostek.

Przykład 6

Dana jest funkcja produkcji Y = 2·(KL)^0,5. Zbadać czy spełnia ona warunki nałożone na funkcję produkcji? Obliczyć f_K , f_L , KSS dla K = 1, L = 4.

Znaczącą rolę w ekonometrii odgrywa funkcja produkcji Cobba-Douglasa postaci:

Y = a₀·X₁^a1· X₁^a2·… X₁^an· ;

gdzie a_i > 0 dla 0 ≤ i ≤ n. Jest to przykład potęgowego modelu ekonometrycznego.

Zbadamy funkcję produkcji Cobba-Douglasa dla przypadki dwuwymiarowego:

Y = a·K^b·L^c· ; dla a>0 ; 0 < b, c < 1.

Do estymacji parametrów strukturalnych wykonujemy transformację logarytmiczną i dostajemy:

ln(Y) = ln(a) + b·ln(K) + c·ln(L) +  ;

Czy spełnia ona wymogi nakładane na funkcję produkcji?

1. f_K = a·b·K^b-1·L^c > 0 ; f_L = a·c·K^b·L^c-1 > 0 ; produkcyjności krańcowe są dodatnie

2. f_KK = a·b·(b-1)·K^b-2·L^c < 0 ; f_LL = a·c·(c-1)·K^b·L^c-2 < 0 ; produkcyjności krańcowe są malejące

3. f_KL = f_LK = a·b·c·K^b-1·L^c-1 > 0; produkcyjność jednego czynnika rośnie przy zwiększeniu nakładów drugiego;

4. f(d·K, d·L) = d^b+c ·f(K,L); czyli jest jednorodna stopnia (b+c);

5. KSS = -(f_L/f_K) = -(cK/bL) = -(c/b)·U ; gdzie U = K/L to współczynnik technicznego uzbrojenia pracy,

W3 aa nieliniowe.doc W3

3/7

---