KLASYCZNY MODEL REGRESJI LINIOWEJ
A SFORMUŁOWANIE MODELU
Wartości oczekiwane warunkowych rozkładów zmiennej losowej Y są liniową funkcją ustalonych wartości zmiennej losowej X:
![]()
przy czym wariancja zmiennej losowej Y w jej warunkowych rozkładach jest stała (niezależna od x):
![]()
Klasyczny model normalnej regresji liniowej
Warunkowe rozkłady zmiennej losowej Y są normalne:
Y dla X=x ma rozkład ![]()
B SFORMUŁOWANIE MODELUZałożenie
Ciąg par ![]()
jest n-elementową próbą losową z populacji dwuwymiarowej, stanowiącą podstawę estymacji parametrów zależności zmiennej Y od z góry ustalonych wartości zmiennej X.
Postać klasycznego modelu regresji liniowej
![]()
![]()
gdzie:1. ![]()
2. ![]()
3. ![]()
dla ![]()
Klasyczny model normalnej regresji liniowej
4. ![]()
![]()
WNIOSKI Z ZAŁOŻEŃ DOTYCZĄCYCH ROZKŁADU ZMIENNYCH LOSOWYCH ![]()
a)
- ![]()
![]()
funkcja regresji I rodzaju Y względem X jest
liniowa
- wartości zmiennej
X są niezależne
Dowód:
![]()
b)![]()
wariancje w warunkowych rozkładach zmiennej Y są takie same
Dowód:![]()
c)- ![]()
dla ![]()
składniki losowe są nieskorelowane
d)
- ![]()
![]()
warunkowe rozkłady zmiennej losowej Y są normalne
B ESTYMACJA PARAMETRÓW KLASYCZNEGO MODELU REGRESJI LINIOWEJ
B 1 ESTYMACJA PARAMETRÓW STRUKTURALNYCH MODELU:
i
z populacji dwuwymiarowej ![]()
pobieramy n-elementową próbę losową ![]()
wynikom próby (zbiorowi par wartości ![]()
), przyporządkowujemy zbiór n-punktów na płaszczyźnie o współrzędnych równym obserwowanym wartościom obu cech,
do danych z próby (do zbioru n-punktów na płaszczyźnie) tak dobieramy równanie linii prostej, aby jej wykres możliwie dobrze "pasował" do punktów reprezentujących na wykresie poszczególne obserwacje z próby:
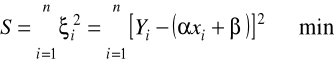
różniczkujemy wyrażenie S względem i , otrzymując:
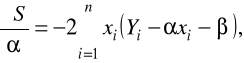
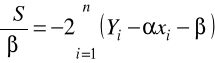
przyrównujemy pochodne do zera, zastępując jednocześnie przez ![]()
i przez ![]()
, otrzymując układ równań:
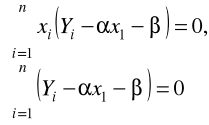
przekształcamy układ równań uzyskując tzw. układ równań normalnych:
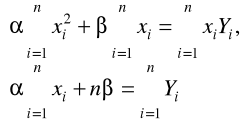
rozwiązujemy układ równań względem ![]()
i ![]()
otrzymując:
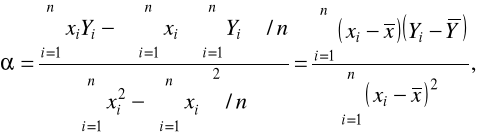
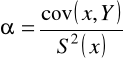
,
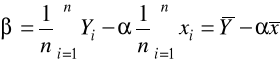
B 2 ESTYMACJA PARAMETRÓW STOCHASTYCZNYCH MODELU: ![]()
i ![]()
1. Estymacja wariancji składników losowych ![]()
wariancja reszt:
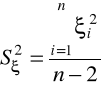
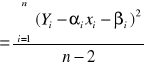
odchylenie standardowe reszt:
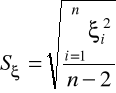
2. Estymacja standardowych błędów oceny parametrów i
estymator standardowego błędu oceny parametru :
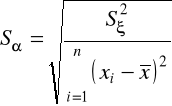
estymator standardowego błędu oceny parametru :
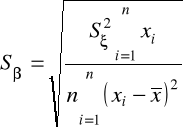
LINIOWA FUNKCJA REGRESJI WYZNACZANA
Z PRÓBY LOSOWEJ
Postać liniowej funkcji regresji wyznaczanej z próby losowej:
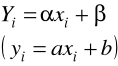
Reszty modelu regresji: 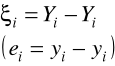
WŁASNOŚCI LINIOWEJ FUNKCJI REGRESJI
WYZNACZONEJ ZA POMOCĄ MNK
suma wartości teoretycznych zmiennej zależnej jest równa sumie empirycznych wartości tej zmiennej
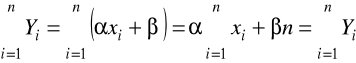
suma reszt równa jest zeru
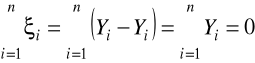
wykres funkcji regresji z próby przechodzi zawsze przez punkt o współrzędnych ![]()
![]()
DOKŁADNOŚĆ DOPASOWANIA PROSTEJ MNK
Równość wariancyjna
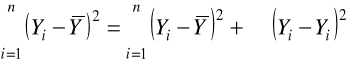
Współczynnik determinacji ( w tym przypadku - kwadrat współczynnika korelacji)
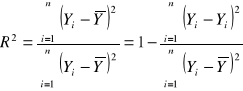
R2= r2 (tylko w regresji liniowej)
![]()
Współczynnik indeterminacji
![]()
WNIOSKOWANIE W KLASYCZNYM MODELU NORMALNEJ REGRESJI LINIOWEJ
stawiamy hipotezę, że współczynnik regresji ![]()
przyjmuje określoną wartość liczbową ![]()
:
![]()
stawiamy hipotezę alternatywną:
![]()
jeżeli ![]()
jest prawdziwa, to statystyka: ≠
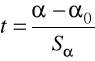
ma rozkład t-Studenta z n-2 stopniami swobody,
przy danym z góry poziomie istotności ![]()
obszar krytyczny tej statystyki określony jest wzorem:
![]()
jeżeli wartość statystyki t oszacowana na podstawie próby losowej:
- należy do obszaru krytycznego ![]()
to ![]()
odrzucamy na korzyść ![]()
,
- nie należy do obszaru krytycznego ![]()
to stwierdzamy, że nie ma podstaw do odrzucenia ![]()
.
ESTYMACJA NA PODSTAWIE KLASYCZNEGO MODELU REGRESJI LINIOWEJ
dokonujemy estymacji, opierając się na klasycznym modelu regresji liniowej, warunkowej wartości oczekiwanej zmiennej losowej Y przy warunku, że X=x, tzn. estymacji ![]()
:
![]()
najlepszym nieobciążonym estymatorem liniowym warunkowej wartości oczekiwanej ![]()
jest zmienna losowa ![]()
o postaci:
![]()
,
wariancja estymatora ![]()
wyraża się wzorem:
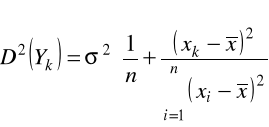
estymatorem wariancji ![]()
jest ![]()
określona wzorem:
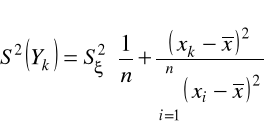
PREDYKCJA NA PODSTAWIE KLASYCZNEGO MODELU REGRESJI LINIOWEJ
dokonujemy estymacji, opierając się na klasycznym modelu regresji liniowej, pojedynczej wartości zmiennej losowej Y przy ustalonej wartości ![]()
:
![]()
,
najlepszym nieobciążonym estymatorem pojedynczej wartości zmiennej losowej ![]()
jest statystyka o postaci:
![]()
błąd predykcji pojedynczej realizacji zmiennej losowej ![]()
jest sumą dwóch nieskorelowanych błędów:
- błędu estymacji warunkowej wartości oczekiwanej zmiennej losowej Y,
- odchyleń pojedynczych realizacji zmiennej w rozkładzie warunkowym od średniej tego rozkładu,
błąd predykcji (wariancja) wyraża się wzorem:
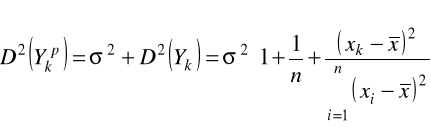
estymator (średniego) błędu predykcji (odchylenia standardowego) określamy jako:
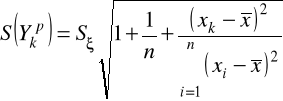
Wyszukiwarka
Podobne podstrony:
Zarządzanie konfliktami w organizacji i ich rozwiązywanie, EKONOMIA, Zarządzanie, Zarządzanie(1)
Ściąga mikroekonomia, Studia - Administracja Samorządowa, Ekonomia i Zarządzane
Motywowanie - demotywacja pracownika, Sopocka Szkoła Wyższa, Ekonomia, Zarządzanie, dodatek, zagadni
Podmioty gospodarcze, Ekonomia i zarządzanie
Psychologia ekonomiczna(2), Zarządzanie i marketing
Obowiązki pracodawcy, Różne Dokumenty, MARKETING EKONOMIA ZARZĄDZANIE
Reformat-Marketing-ŚCIĄGA IV sem, biznes, ekonomia + marketing i zarządzanie
ZAWIERANIE I ROZWIĄZYW NIE UMÓW O PRACĘ. RODZAJE UMÓW O PRACĘ, Różne Dokumenty, MARKETING EKONOMIA Z
FiR2009-2, Informatyka i Ekonometria SGGW, Semestr 5, Zarządzanie, Kolos
Rozwój funkcji personalnej i geneza zarządzania zasobami ludzkimi, Ekonomia, Zarządzanie kadrami
Spółka partnerska - przepisy, Różne Dokumenty, MARKETING EKONOMIA ZARZĄDZANIE
Ekonomia i Zarządzanie materialy
Fib2008-3, Informatyka i Ekonometria SGGW, Semestr 5, Zarządzanie, Kolos
MAKROEKONOMIA ZAGADNIENIA, Studia - Administracja Samorządowa, Ekonomia i Zarządzane
Cel działalności przedsiębiorstw, Różne Dokumenty, MARKETING EKONOMIA ZARZĄDZANIE
więcej podobnych podstron