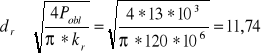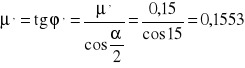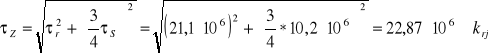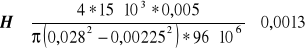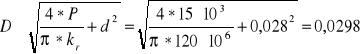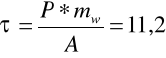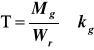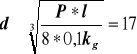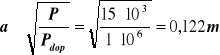PODNOŚNIK ŚRUBOWY TYPU „D” O UDŹWIGU Q =10KN I WYSOKOŚCI PODNOSZENIA WYNOSZĄCEJ H = 0,6 m.

DANE	OBLICZENIA	WYNIKI
Q=10KN H=0,6 m. H=400mm Materiał: stal St4 kr = kc = =120 MPa P = 10 kN ds= 0,0252mm ks=85 MPa kr=120MPa krj=70MPa bmax = 241,9 mm St4 kc=120MPa dr=22,5mm d=28mm Po=0,005m P=10kN d=28mm kr=120MPa mat. St4 St4 R=235MPa μ=1 L=245,2 λp=107	Wyznaczanie wielkości gabarytowych podnośnika Górne maksymalne Dolne minimalne położenie podnośnika położenie podnośnika trapezowego trapezowego H = 600 mm H = 2 L = L = Zakładamy że: amin = 40 mm bmin = 50 mm Obliczam amax 340 mm Stąd: L = = 340^2 + 60^2 = 345,2 mm bmax = = mm 2. Obliczanie sił w poszczególnych prętach kratownicy podnośnika trapezowego. Pręty kratownicy są położone przegubowo jedynie na końcach .Po uwolnieniu ich z więzów na końcach każdego pręta będą działały siły reakcji odpowiednich przegubów. Każdy z prętów kratownicy będzie poddany działaniu sił osiowych, rozciągających bądź ściskających. W celu określenia wartości tych sił rozpatrujemy równowagę sworzni w przegubie A,B. Z racji symetrii układu, równoważne wnioski otrzymaliśmy odpowiednio dla sworzni przegubów C i D. Równanie równowagi sworznia A ∑Pix = S1- sinα - S2 * sinα = 0 S1= S2 ∑Pis = -Q1+ S1 * cosα + S2 * cosα = 0 Q = 2 S1 * cosα Po przekształceniu otrzymujemy ; Siły ściskające działające w zewnętrznych prętach podnośnika są identyczne co wynika z symetrii podnośnika . Obliczenie sił działających w przegubie B ∑Pix = -2 S1sinα + R = 0 R = 2 S1 sinα Jedną siłą nieznaną była siła R stanowiąca reakcję śruby rzymskiej. Zupełnie wystarczające jest jedno równanie równowagi. W celu wyznaczenia obciążeń największych następujących w prętach, oraz śrubie rzymskiej podnośnika obliczamy wszystkie siły w położeniu maksymalnym i minimalnym podnośnika. Obliczam siły w prętach, oraz śrubie rzymskiej podnośnika w położeniu maksymalnym. kN kN Obliczam siły w prętach oraz śrubie rzymskiej podnośnika w położeniu minimalnym. kN kN Obliczam średnicę śruby z warunku na nacisk powierzchniowy Pobl = 1,3 P = 1,3 •10 • 10^3 = 13 kN Przyjmuję materiał śruby stal St4 kr = 120 MPa mm Przyjmuję gwint trapezowy symetryczny dr = 22,5 Tr = 28•5 P = 5 Sprawdzam samohamowność gwintu * = 2,54^o pozorny współczynnik tarcia *' = 0,15 * = 8,82^o* * ** gwint jest samohamowny. Sprawdzam obliczoną średnicę śruby z warunku na ściskanie. MS = 44,3 Nm 21,1 MPa * 120 MPa 10,2 MPa * 85 MPa 22,87 MPa * 70 MPa Obliczam długość śruby. Lśr = 2 * bmax = 2 * 241,9 = 483,8 mm Obliczam wysokość nakrętki z warunku na nacisk Powierzchniowy. Przyjmuję materiał nakrętki stal St4 kc = 120 MPa ko = 0,8 * kc = 0,8 * 120 * 10^6 = 96 MPa m H ≥ 13 mm przyjmuję H = 36 mm Sprawdzam liczbę zwojów 9. Obliczam średnicę zewnętrzną nakrętki z warunku na rozciąganie m D ≥ 30mm przyjmuję D = 48mm Obliczam ramiona podnośnika z warunku na wyboczenie, przyjmujemy pręt stalowy (płaskownik) s=40mm=h g=12mm dla R=253MPa λp=107 obliczam smukłość m dla tego stosunku przyjmuje mw=107 Pole pręta wynosi A=2 * b * h=0,00096m^2 MPa warunek na wyboczenie jest spełniony 11.Obliczam średnicę sworznia z warunku na zginanie mm przyjmuję d=20mm 12.Obliczam średnicę sworznia na nacisk powierzchniowy a) w uchu k0=0,8kc=96MPa MPa * 96MPa b) w piastach widełek k0=0,8kc=96MPa P=21MPa * 96MPa warunek jest spełniony 13.Dobieram podkładkę i zawleczkę do sworznia sworzeń PN-90/M-83002 mat. St4 d=20 D=30 d1=5 k=5 l2=8 R=1 cmax=4 e≅2 b) zawleczki PN-90/M-82004 do=5 d=4,6 D=4,2 l1=10 l2=4 l=28 podkładki PN-90/M-82004 do=20 D=30 g=4 14.Obliczam długość sworznia L = L1 + L2 + g + d0 + f0 L = 48 + 0,5 + 4 + 7 = 60 mm Przyjmuję długość sworznia L = 60 mm 15.Obliczam długość boku podstawy podnośnika przyjmując Pdop = 1 MPa a≥122mm Przyjmuję a = 125 mm	amax = 340mm L = 245,2 bmax = 342,8mm S1a = 5,1kN Ra = 10,13 kN S1b = 65,2 kN Rb = 129,5 kN Pobl = 13 KN dr= 11,74 mm dr = 22,5 mm Tr = 28•5 P = 5 γ = 2,54^o *^'= 8,82 Tr * kr τS * kS τZ * krj Lśr = 483,8 mm H=36mm Z=7 D=48mm d=20mm L=60mm a=125mm

g

g

b_max

f₀

L₁

s

x

A

Q

D

Q

L₂

R

S₁

S₁

x

y

y

A

b_min

B

C

Q

a_min

a_max

Q

Q

Q

Q

L

---