POLITECHNIKA WROCŁAWSKA INSTYTUT FIZYKI		Sprawozdanie z ćwiczenia nr 57
Piotr Wilczewski		Badanie efektu Halla
BLiW rok 2	Data: 17.11.1998		Ocena:

1. Wstęp teoretyczny

W roku 1879 na Uniwersytecie Harward E. H. Hall zaprezentował doświadczenie, które pozwala określić znak ładunku płynącego w przewodniku. Polegało ono na umieszczeniu paska miedzi, w którym płynie prąd o natężeniu i (w określonym kierunku), w polu magnetycznym o indukcji magnetycznej B. Pasek umieszczony był tak między biegunami elektromagnesu, aby linie natężenia pola były prostopadłe do płaszczyzny paska. Pole to działa na pasek z siła F (równą il × B). Ponieważ siła działająca na pasek jest wynikiem sił (równych qv × B), działających na ładunki przenoszące prąd; ładunki te, niezależnie od tego czy są dodatnie, czy ujemne, będą odchylane w jedną stronę, powodując powstanie między przeciwległymi brzegami paska poprzecznej różnicy potencjałów Halla (napięcie Halla). Znak płynących ładunków jest określony przez znak wytworzonej różnicy potencjałów.

Załóżmy, że nośnikami prądu są elektrony. Jeżeli przez płytkę płynie prąd o natężeniu I_s, a pola magnetycznego nie ma, to wówczas elektrony poruszać się będą w kierunku przeciwnym do kierunku prądu ze średnią prędkością v. Jeżeli teraz pojawi się pole magnetyczne o indukcji B, to na elektrony poruszające się w tym polu z prędkością v będzie działać siła Lorentza F_L= -e(v × B). W skutek zakrzywienia torów elektrony gromadzą się na jednej krawędzi płytki, natomiast na drugiej wytwarza się niedobór elektronów. Dzięki temu w płytce powstaje poprzeczne, w przybliżeniu jednorodne pole elektryczne o natężeniu E. Pole to działa na elektrony siłą F_E = -eE. Dla warunków równowagi możemy zapiać F_L= F_E i wówczas napięcie Halla określa równanie:

gdzie , przy czym n oznacza koncentrację elektronów swobodnych, d zaś jest grubością płytki, e to ładunek elemnetarny.

2. Część pomiarowa

2.1. Pomiar napięcia Halla dla stałej wartości natężenia I_S prądu płynącego przez cewkę, równego 5 mA.

Tabela pomiarowa

Im [mA]	30	44	59	74	89	103	118	132	148
ΔIm [mA]	1.0	1.0	1.0	1.0	5.0	5.0	5.0	5.0	5.0
UH [mV]	53.54	77.71	103.9	130.7	157.6	184.4	212.4	239.7	267.4
ΔUH [mV]	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1
IS [mA]	5.0	5.0	5.0	5.0	5.0	5.0	5.0	5.0	5.0
B [T]	0.1	0.15	0.2	0.25	0.3	0.35	0.4	0.45	0.5
ΔB [T]	0.002	0.003	0.004	0.005	0.006	0.007	0.008	0.009	0.010
γ [V/AT]	107.08	103.61	103.90	104.56	105.07	105.37	106.20	106.53	106.96
Δγ [V/AT]	3.198	3.035	3.009	3.008	3.009	3.008	3.024	3.027	3.035

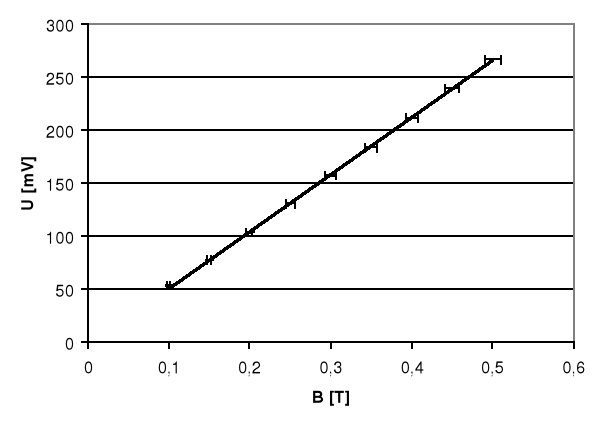
2.2. Wykres zależności U_H = f(B), dla I_S = 5 mA

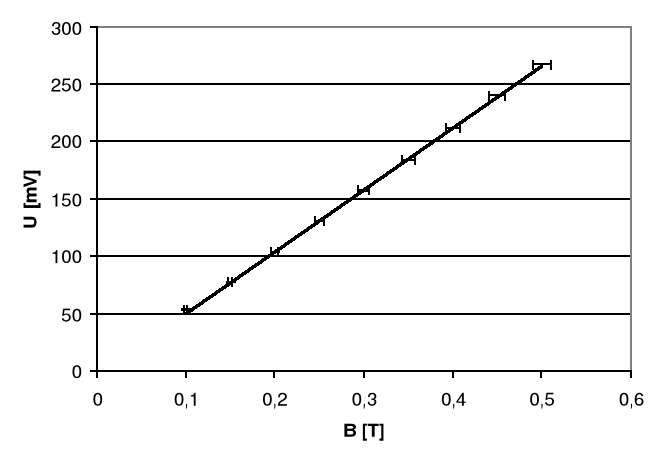
2.3. Przykładowe obliczenia.

a) błąd cechowania elektromagnesu B, gdzie B/B = 2% :

B = B 2% = 0,1×0,02 = 0,002 T

b) błąd prądu magnesującego Im:

Im = ( klasa × zakres) / 100 = ( 0,5 200 ) / 100 = 1 mA

c) błąd napięcia Halla UH:

UH = ( klasa × zakres ) / 100 = 0,1 mV

d) czułość hallotronu :

= UH / IS B = 0,0535 / ( 0,0050,1 ) = 107,08 V/AT

e) błąd czułości hallotronu wyznaczony metodą różniczki logarytmcznej:

= UH / IS B

ln = ln UH - ln IS - ln B

d/ = dUH/UH + dIS/IS + dB/B

/ = UH/UH + IS/IS + B/B = ,

gdzie - błąd względny

= = ( 0,1/53,4 + 0,04/5 + 0,002/0,1 )107,08 = 3,198 V/AT 3,20 V/AT

4. Pomiar napięcia Halla dla stałej wartości B = 0,5 T i zmiennego natężenia prądu płynącego przez cewkę

Im [mA]	148	148	148	148	148	148	148	148	148
ΔIm [mA]	5.0	5.0	5.0	5.0	5.0	5.0	5.0	5.0	5.0
UH [mV]	51.01	77.75	103.7	129.6	155.7	181.6	207.0	241.0	267.4
ΔUH [mV]	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1
IS [mA]	1.0	1.5	2.0	2.5	3.0	3.5	4.0	4.5	5.0
B [T]	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5
ΔB [T]	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010
γ [V/AT]	20.40	31.10	41.48	51.84	62.28	72.64	82.80	96.40	106.96
Δγ [V/AT]	1.264	1.491	1.699	1.906	2.116	2.323	2.524	2.825	3.035

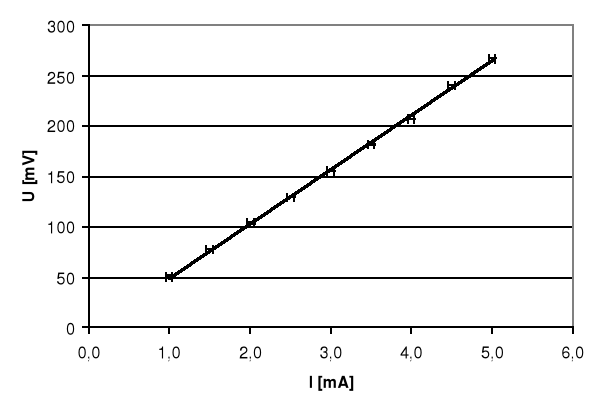
2.5 Wykres zależności U_H = f(I_S)

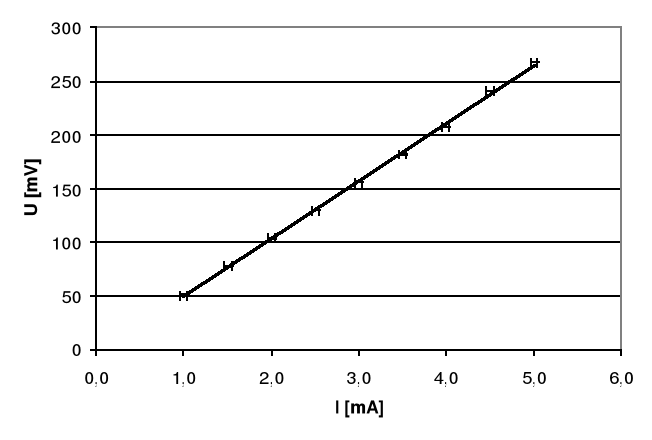
3. Obliczenie koncentracji elektronów swobodnych

Korzystając z otrzymanych danych obliczono koncentrację elektronów swobodnych ze wzoru :

n = 1 / e d ,

gdzie: e = 1,6 10-19 C;

d = 0,1 mm ( grubość płytki );

= 105,48 V/AT

= 3,04 V/AT

d/d = 1%

n = 1 / ( 1,6×10-19 × 105,48 × 0,1×10-3 ) = 2,70×1021

Obliczanie wartości błędu bezwzględnego n metodą różniczki logarytmicznej:

n/n = ( / + d/d ) = - błąd względny

n = ( / + d/d ) n = 1,05 1020

4. Wnioski

Efekt Halla zachodzi w metalach i półprzewodnikach. W metalach i półprzewodnikach typu n nośnikami są elektrony, one są więc odpowiedzialne za powstanie napięci Halla. W półprzewodnikach typu p nośnikami są dziury (ładunki dodatnie). W takim przypadku zmieni się polaryzacja napięcia Halla, ze względu na przeciwnie skierowaną siłę Lorentza i równoważącą ją siłą wynikłą z pola poprzecznego (napięcia Halla).

W przypadku płytki metalowej i wykonanej z półprzewodnika typu n różnice z zachowaniu się układu będą spowodowane różną ilością elektronów swobodnych w tych materiałach.

Ze wzoru na czułość hallotronu wynika, iż przy wzroście koncentracji elektronów czułość maleje, w rezultacie mamy do czynienia z mniejszym poziomen napięć Halla.

4

---