POLITECHNIKA RZESZOWSKA Im. Ignacego Łukasiewicza WYDZIAŁ BUDOWY MASZYN I LOTNICTWA KATEDRA PRZERÓBKI PLASTYCZNEJ |
TOMCZYK WOJCIECH
Wydz.BMiL Spec.PDF Gr.lab.1411 Sem.czwarty Rok akad.2002/2003
|
||
Ćwiczenie odrobiono dn. ……………………….. |
Sprawozdanie przyjęto dn. ……………. |
Podpis …………………… |
Uwagi …………………….. |
LABORATORIUM OBROBKI PLASTYCZNEJ
LABORATORIUM
Sprawozdanie z ćwiczenia nr 1
Temat: Wyznaczanie krzywych umocnienia metali w próbie
jednoosiowego rozciągania.
RZESZÓW 2003-03-02
1.)Cel ćwiczenia
Celem ćwiczenia jest poznanie odkształceń podczas jednoosiowego
rozciągania próbek wykonanych z różnych materiałów oraz wyznaczenie równania opisującego umacnianie materiału.
2.)Rozciąganie próbki trójstopniowej (metoda Heyera).
Wartość stałych C i n oblicza się na podstawie wyznaczonych doświadczalnie współrzędnych dwóch punktów krzywej umocnienia , przy czym zadaniem próby rozciągania jest określenie współrzędnych tylko tych punktów.
Kształt i wymiary próbki stosowanej w metodzie Heyera przedstawiono na rys.1.
Część środkowa próbki składa się z trzech odcinków A,B,C, różnej szerokości bo:boB.=1.01 boA ,boC = 1.1 boA .Aby umożliwiać dokładne określenie odkształceń eB i ec , nanosimy na odcinkach B i C bazy pomiarowe l0B i l0C . Po rozciągnięciu próbki aż do momentu wyraźnego przewężenia lub zerwania w części A odczytujemy wartość siły maksymalnej i mierzymy długość odcinków lB i lC . Szukane wartości odkształceń obliczamy jako:
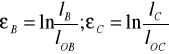
![]()
Naprężenia uplastyczniające , odpowiadające obliczonym odkształceniom , są równe naprężeniom rozciągającym , które występują w tych częściach próbki w fazie końcowej rozciągania :
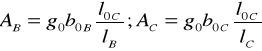
gdzie AB i AC oznaczają pola odpowiednich przekrojów poprzecznych próbki , które można określić z warunków stałej objętości odcinków pomiarowych :
Korzystając przyjętego równania krzywej umocnienia dla materiałów wyżarzonych , obliczamy odpowiednie wartości naprężeń :
![]()
Wykorzystując dane zależności oraz fakt , że wartość siły maksymalnej rozciągającej część B i C próbki była taka sama , obliczamy wartości stałych materiałowych n i C :
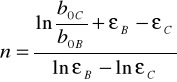
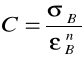
3.)Wyniki pomiarów :
Lp. |
Materiał |
Wymiary próbki przed zerwaniem [mm] |
Maksymalna siła zrywająca [kN] |
Wymiary próbki po zerwaniu [mm] |
|||||
|
|
go |
boB |
boC |
loB |
loC |
Pmax |
lB |
lC |
1 |
Stal Niskowęglowa
|
1 |
15,57 |
17,0 |
20,2 |
20,45 |
5,5 |
23,15 |
21,75 |
2 |
Aluminium
|
1 |
14,8 |
16,45 |
20,1 |
20,25 |
3,9 |
22,35 |
20,95 |
3 |
Miedź
|
1 |
15,0 |
16,55 |
20,3 |
20,25 |
1,05 |
23,0 |
22,0 |
Dla Fe
![]()
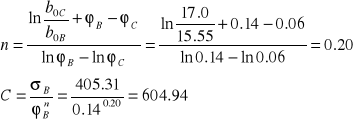
![]()
Dla Cu:
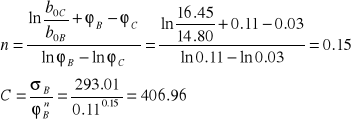
Dla Al.:
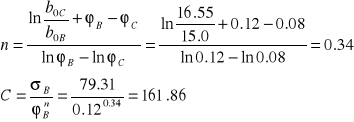
4.)Zestawienie wyników.
|
sFe [MPa] |
sCu [MPa] |
sAl [MPa] |
0.1 |
381.69 |
288.11 |
73.98 |
0.2 |
438.45 |
319.67 |
93.65 |
0.3 |
475.48 |
339.72 |
107.49 |
0.4 |
503.64 |
354.70 |
118.53 |
0.5 |
526.63 |
366.77 |
127.88 |
0.6 |
546.19 |
376.94 |
136.05 |
0.7 |
563.29 |
385.76 |
143.37 |
0.8 |
578.54 |
392.56 |
150.03 |
0.9 |
592.33 |
400.58 |
156.16 |
1 |
604.94 |
406.86 |
161.86 |
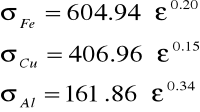
5.)Wykres:
6.) Wnioski:
Krzywa umocnienia dla miedzi wydaje się być bardziej stroma niż żelaza czy aluminium czyli dla tych samych odkształceń występowały dużo większe przyrosty naprężeń. Spowodowane to było większą plastycznością materiału , a co za tym idzie dużo szybciej się umacniał.
Legenda:
![]()
naprężenie uplastyczniające,
![]()
C - stała materiałowa,
![]()
odkształcenie rzeczywiste,
n - wykładnik krzywej umocnienia wyznaczony doświadczalnie,
A - pole powierzchni przekroju poprzecznego próbki .
![]()
![]()
![]()
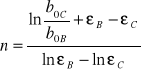
![]()
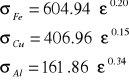
Wyszukiwarka
Podobne podstrony:
Wyznaczanie krzywej umocnienia materiału - sprawko, Uczelnia, Techniki wytwarzania
Cel wyznaczania krzywej umacniania, Uczelnia, Techniki wytwarzania
Materiałoznawstwo i Techniki Wytwarzania Struktury
Materiałoznawstwo i Techniki Wytwarzania Plan Laboratoriów
żelazo węgiel, techniki wytwarzania z materiałoznawstwem
obróbka rezcna, WIEDZA, BHP, techniki wytwarzania
cichosz,podstawy technik wytwarzania, Przepisy BHP przy spawaniu gazowym
techniki wytwarzania 4 03 13
Praca semestralna techniki wytwarzania sem II
Materiałoznawstwo i Techniki Wytwarzania Sprawozdanie 5D
Techniki wytwarzania-drewno, Ukw, II Lic, Drewno, Wyk�?ady
Materiałoznastwo- odpowiedzi, PG inżynierka, Semestr 1, Materiałoznawstwo i techniki wytwarzania
Specjalne metody tloczenia, Studia, Techniki wytwarzania
Materiał2, Politechnika, Sprawozdania, projekty, wyklady, Techniki wytwarzania
Materiałoznawstwo i Techniki Wytwarzania Sprawozdanie 5A
Materiałoznawstwo i Techniki Wytwarzania Sprawozdanie 3B
Materiałoznawstwo i Techniki Wytwarzania Sprawozdanie 6B
cichosz,techniki wytwarzania,Obróbka elektrochemiczna?M
więcej podobnych podstron