1.Pojęcie zbioru wypukłego, funkcji wypukłej, otoczki wypukłej zbioru.

X rzeczywista przestrzeń liniowa. Mówimy, że zbiór C
X jest zbiorem wypukłym

x,y
C odcinek [x,y]
C

[x,y] odcinek domknięty o końcach x i y

[x,y] : = {z
X ׀ z =
_x + (1-
y) }

0

<1

Zbiór pusty z definicji jest zbiorem wypukłym.

Stwierdzenie:

(At) _t€T dowolna indeksowana rodzina zbiorów wypukłych przestrzeni X,Ť dowolny zbiór skończony lub nieskończony
A_t wypukły podzbiór X

wtedy
A_t jest wypukłym zbiorem w X

x€A_t

ω (X)rodzina wszystkich wypukłych podzbiorów przestrzeni X

C
X, coC lub conrC czytamy: otoczka wypukła zbioru C.

coC:=
A A€ ω (X)

coC- otoczka wypukła zbioru C jest to przecięcie (część wspólna, iloczyn) wszystkich zbiorów wypukłych zawierających zbiór C. Jest to najmniejszy zbiór wypukły zawierający zbiór C.

Pojęcie funkcji wypukłej.

X - rzeczywista przestrzeń liniowa

f: X →¯R= R
{
,
}

z funkcją f są związane dwa zbiory:

dom f - efektywny zbiór funkcji f

dom f:= {x € X | f(x) <
}

epi f - epigraf funkcji f (nadwykres funkcji f)

epi f:= {(x,
) € X
R|

Niech f: X → ¯R

Mówimy, że funkcja f jest funkcją wypukłą, jeżeli epif jest zbiorem wypukłym

Mówimy, że funkcja f: X → ¯R jest funkcją właściwą, jeżeli Vx € X f(x)>-∞ oraz domf ≠Ø (to oznacza że f
+∞ (nie jest tożsamościowo równa +∞)

TWIERDZENIE:

Niech f: X → ¯R właściwa funkcja, gdzie X rzeczywista przestrzeń liniowa wtedy są równoważne następujące warunki:

1)
n € N

,
…
€ domf

,
,……

zachodzi nierówność Jensena

f (
)≤
f(x_i)

2)

,
€ domf

zachodzi nierówność Jensena

f(
)≤
-warunek 2 geometrycznie oznacza że wykres funkcji y = f(x) leżące pomiędzy prostymi pionowymi o równaniach x =
i x =
leży poniżej odcinka łączącego punkty (
,f(
) i (
,f(
)

3) epif jest zbiorem wypukłym

STWIERDZENIE

a) (f _t ) _t€T dowolna indeksowana rodzina właściwych funkcji wypukłych określonych na przestrzeni liniowej X o wartościach w ¯R, T - dowolny zbiór skończony lub nieskończony wtedy funkcja f =
jest funkcją wypukłą

f =
(x) jest funkcją wypukłą (f =
(x)
x€X)

b)
,..,
wypukłe właściwe funkcje określone na X o wartościach w ¯R wtedy funkcja
jest właściwą funkcją wypukłą tzn. suma skończonej liczby funkcji wypukłych jest funkcją wypukłą.

: X → ¯R wypukłe właściwe funkcji

f = max{
}

x € X f(x) = max {
(x),
(x)} wtedy f jest właściwą wypukłą funkcją

epif = epi
∩ epi

epif = ∩ epif_t

2.Zadanie programowania wypukłego i sformułuj twierdzenie KUNATUCKERA.

Zadanie programowania wypukłego

X- rzeczywista przestrzeń liniowa

A- nie pusty zbiór wypukły w X

fi: X → ¯R i = 0,1,…..m

Zadaniem programowania wypukłego nazywamy następujące ekstremalne zadania:

(P) f_o (x)
min,

f_i (x)
0, i=1,2,…,m x
A

Dp - zbiór elementów dopuszczalnych z zadania P

Dp: {x
X │f_i (x)
0, i=1,2,…,m }

x
А}

Punkt
- punkt
jest absolutnym minimum z zadania P

α
gdzie

R ^m+1

Funkcja α (x,
) nazywamy funkcją Lagrange^'a zadania (P).

Liczby
i,i = 0,1,…,m nazywamy mnożnikami Lagrange^'a.

Wektor
= (
o,
1,….,
m) nazywamy wektorem mnożników Lagrange^'a.

Uwaga - ograniczenie x
А nie wchodzi do funkcji Lagrange^'a.

Twierdzenie KUHNA-TUCKERA

1.Niech
będzie absolutnym minimum w zadaniu (P), gdzie P to zadanie programowania wypukłego wtedy istnieje
^m+1

taki, że dla funkcji Lagrange^'а zadania (P) zachodzą następujące warunki:

а) min α(x,
) = α

x
А

Zasada minimum funkcji Lagrange^'а

b) warunki komplementarności
in

c) warunki nieujemności
in

2. Jeżeli
(jest elementem dopuszczalnym zadania(P))i są spełnione warunki а) - c) z

3. Jeżeli
i są spełnione warunki а) - c) oraz zachodzi warunek SLATERA

to

Uwaga. Dla zadania wypukłego programowania idea Lagrange^'а uzyskała najbardziej doskonałą postać. Punkt
będący rozwiązaniem wypukłego zadania jest punktem minimum funkcji Lagrange^'а (dotyczy warunku а)). Warunki b) i c) są charakterystyczne dla zadań z ograniczeniami nierównościowymi. Warunek konieczny na absolutne minimum w zadaniu programowania wypukłego jest bliski warunkowi dostatecznemu. Warunek konieczny pokrywa się z warunkiem dostatecznym, jeśli
jest różna od 0(
).

3. Sformułuj gładkie skończenie wymiarowe zadania ekstremalne z ograniczeniami równościowymi oraz dla tego zadania sformułuj zasadę nośników Lagrang'ea.

Niech f_i:Rⁿ→R, i=0,1,2…m Funkcja n zmiennych rzeczywistych o wartościach rzeczywistych. Zakładam, że funkcja f_i; i=0,1,2…n₁ spełnia pewien warunek gładkości tzn. są różniczkowane w określonym sensie. Gładkie skończenie wymiarowe zadanie ekstremalne z ograniczeniami równościowymi nazywamy następujące zadanie(P):

f₀(x)→extr f_i(x)=0 , i=1,2…m
Przez rozwiązanie pełne zadania P nazywamy: znalezienie lokalnych ekstremum zadania tj. lokalnych minimów i lokalnych maksimów, znalezienie absolutnego min. i maks., oraz określenie wartości minimalnej i maksymalnej zadania. Dp- zbiór elementów dopuszczalnych zadania P
Dp=
ⁿ
f_i(x)=
i=1,2…m
x=(x₁,x₂...x_n)
Rⁿ
||x||- norma wektora X
||x||=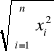

Norma określa odległość (metryka)
x=(x₁,x₂…x_n)
y=(y₁,y₂…y_n)
d(x,y)=||x-y||=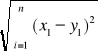


є locmin(P) - punkt
jest lokalnym minimum w zadaniu (P)

єDp


f₀(x)
₀(
)
K(
,
- kula otwarta o środku
i promieniu

K(
,
ⁿI||x-
||

locmax (P)


_^
f₀(x)
f₀ (
)
Lokalne minima i lokalne maksima z zadnia (P) nazywamy lokalnymi ekstremalnymi zadaniami (P)


absmin (P)
f₀(0)
f₀(
)


absmax(P)


f₀(x)
f₀(
)

Funkcja Lagrang'ea z zadania (P)
Funkcja
₀,λ_1,…λ_m)
<sup>m+1

n</sup>_i=oλ_if_i(x)
Funkcje
(x,λ) określoną powyżej nazywamy funkcją Lagrang'ea zadania (P)
wektor λ=(λ₀,λ₁…λ_m)
^m+1nazywamy wektorem mnożników Lagrang'ea liczbę λ_i, i=0,1…m nazywamy mnożnikami Lagrang'ea.
Warunek konieczny pierwszego rzędu na lokalne ekstremum dla gładkiego zadania z ograniczeniami równościowymi - zasada Lagrang'ea.
Niech

locextr(P) a funkcje f_i, i=0,1…m są ciągle różniczkowane w pewnym otwartym otoczeniu punktu
(warunek gładkości) wtedy istnieje niezerowy wektor nośników Lagrang'ea. Λ=(λ_0,λ₁…λ_n)
R^m+1 , λ
0 taki że dla funkcji Lagrang'ea z zadania (P)
(x,λ) = ∑^m_i=0 λ_if_i(x) zachodzi warunek stacjonarności tzn.
1≤ j ≤ n
x_j(
,λ)=0

x_j (
,λ)- pochodna cząstkowa funkcji Lagrang'ea po x_j w punkcie (
,λ)

4. Sformułuj gładkie skończenie wymiarowe zadanie ekstremalne z ograniczeniami równościowymi i nierównościowymi i dla tego zadania sformułuj zasadę mnożników Lagrangea.

Niech f₁:Rⁿ→R , i=0,1,2....m funkcji n zmiennych nieistniejących odwzorowujących Rⁿ w R. Założenie że funkcje f_i, i=0,1,2…n spełniają warunek gładkości. Gładkim skończenie wymiarowym zadaniem ekstremalnym z ograniczeniami równościowymi i nierównościowymi nazywamy następujące zadanie (P)szukamy ekstr. f₀(x)→min
f_i(x)≤0 , i =1,2…m'
f_i(x)=0 , i = m'+1,…m

Warunek konieczny I rzędu na lokalne ekstremum w gładkim skończenie wymiarowym zadaniu ekstremalnym z ograniczeniami równościowymi i nierównościowymi - zasada Lagrangea.

Niech

loc min (P) - punkt lokalnego minimum w zadaniu (P), a funkcje f_i, i= 0,1,...,m są ciągle różniczkowalne w pewnym otoczeniu punktu
(warunek gładkości).Wtedy istnieje niezerowy wektor mnożników Lagrangea

λ= λ₀, λ₁, ...,λ_m
R ^m+1 λ ≠ 0 taki, że dla funkcji lagrangea zad. (P)

λ= λ₀, λ₁, ...,λ_m
R ^m+1 λ ≠ 0 taki, że dla funkcji lagrangea zad. (P)

(x, λ) = ^ (x₁,...,x_n), (λ₀,...,λ_n) = ∑^m_i=0 λ_i f_i (x) = ∑^m_i=0 λ_i f_i (x₁, x₂,...,x_m)

zachodzą następujące warunki

a)warunki stacjonarności

_xj (
, λ) = 0
1≤ j ≤ n

b)warunki komplementarności

λ^_i* f_i (
)= 0 i= 1,2...,m'

c) warunki nieujemności

λ^_i ≥ 0 i= 0,1,...,m'

5.Pojęcie słabej relacji preferencji, silnej relacji preferencji i relacje obojętności Libiparenza.

W zbiorze X jest określona relacja słabej preferencji, oznaczona symbolem ≥.

≥ nazywamy relacją słabej preferencji X jeśli spełnia ona następujące warunki:

1. dla każdego x, y, z € x ( x ≥ y ^ y ≥ z ) wtedy ( x ≥ z) - przechodność

2. dla każdego x, y, z € x ( x ≥ y ) v ( y ≥ z ) - spójność

3. dla każdego x € x, x ≥ x - zwrotność.

(X,≥), gdzie x to zbiór dopuszczalnych koszyków, a ≥ to relacja słabej preferencji.

Relacja słabej preferencji ≥ określa:

a ) relacje silnej preferencji >

x > y wtedy, gdy ( x ≥ y ) ^ nie jest prawdą, że( y ≥ x ) - koszyk x jest silnie preferowany nad koszyk y, ( koszyk x jest lepszy niż koszyk y) wtedy i tylko wtedy, gdy koszyk x jest słabo preferowany nad y i nieprawdą jest, że koszyk y jest preferowany nad koszyk x.

b ) relacja ~ oboistotności (identyczności)x

x ~ y - koszyki x i y są jednakowo dobre

x ~ y wtedy i tylko wtedy, gdy ( x ≥ y ) ^ ( y ≥ x )

c ) relacja obojętności „~” w X jest relacją równoważności tzn. jest zwrotna dla każdego x € X x ~ x :

1. syntetyczna dla każdego x, y € X x ~ y wtedy y ~ x

2. przechodna dla każdego x, y, z € X ( x ~ y ^ y ~ z ) wtedy ( x ~ z )

x € X

zbiór k _x:={y € x / y ~ x } nazywamy obszarem obojętności w przestrzeni towarów X.

6.Pojecie funkcji użyteczności.

Def. (X,≥) - pole preferencji.

Funkcję U:X→R nazywamy funkcją użyteczności odpowiadającą relacji preferencji ≥,jeśli dla każdego x, y € X (x ≥ y)wtedy i tylko wtedy, gdy( u(x) ≥ u(y) ).

Bezpośrednio z powyższej definicji f. użyteczności wynika następujące twierdzenie:

U:X→R

1.Dla każdego x, y € X u(x)=u(y) wtedy i tylko wtedy, gdy x ~ y

2.Dla każdego x, y € X u(x)>u(y) wtedy i tylko wtedy, gdy x > y

Jeżeli U:X→R jest f. użyteczności odpowiadającą relacji preferencji ≥, to funkcja U:X→R określone wzorem:

1) u(x)=au(x)+(0;a,b)> 0

2 u(x)=(1+a)^bn(x) a, b> 0 są funkcjami użyteczności odpowiadającymi relacji preferencji.

(X, Y, Z) - dowolne zbiory f:X→Y , g:Y→Z , h:X→Z

Dla każdego x € X h(x) =g( f(x) ) h=g*f - złożenie funkcji g i f

Twierdzenie jeżeli u : X → R jest funkcją użyteczności odpowiadającą relacji preferencji ≥ a funkcja g : R → R jest rosnąca to funkcja niemalejąca funkcja złożona, że u=g*u jest funkcją użyteczności odpowiadającą relacji preferencji ≥.

7. Zdefiniuj pojęcie ciągłej relacji preferencji, monotonicznej i ściśle wypukłej relacji preferencji.

Dla każdego 1 ≤ i ≤ m relacja preferencji ≥ _i jest ciągła, monotoniczna i ściśle wypukła.

Mówimy, że relacja preferencji ≤ _i jest ciągła, jeśli dla każdego x € R ₊

zbiory {x € R}

{y ≥ x} {z {x > y} są domknięte w lR₊

Mówimy, że relacja preferencji ≥ ( w lR₊) jest monotoniczna wtedy i tylko wtedy, gdy x, z € lR₊ x + z ≥ x .

Mówimy, że relacja preferencji ≤ lR₊ jest ścisle wypukła jeśli dla każdego ƛ € ( 0;1) dla każdego x € lR₊^l ( y ≥ x ^ y ≠ x ) wtedy ( ƛ _y + ( 1- ƛ ) x >

8. Sformułuj twierdzenie Arowa o dyktaturze i wyjaśnij wszystkie pojęcia występujące w sformułowaniu tego twierdzenia.

„m” praw dyktatora odpowiadające „m” uczestnikom to jedyne prawa określające grupowy wybór spełniające aksjomat niezależności i jednomyślności. Jedyną relacją grupowej preferencji spełniającą aksjomat jednomyślności i aksj. Niezależności jest dyktatura. Przyjmiemy następujące założenia odnoszące się do prawa określającego grupowy wybór P.

Tw. Arowa można sformułować następująco: 6 warunków:

1.relacja spójna, tzn. że dla każdego x, y € R (x ≥_s y ) v (y ≥_s x )

2. relacja przechodnia, tzn. że dla każdego x, y, z € R (x ≥_s y)^( y ≥_s z) wtedy (x ≥_s z)

3. ≥_s=P (≥_1, ≥_2, …≥_m) wtedy mówimy, że P jest prawem określającym grupowy wybór. Istnieje kilka naturalnych warunków nakładanych na P:

4.Aksjomat jednomyślności-jeżeli wszyscy uczestnicy preferują x nad y, to grupa preferuje x nad y.

(dla każdego 1≤ i ≤ m X ≥_i Y) wtedy (X ≥_s Y)

5.Aksjomat niezależności-przy porównaniu alokacji x i y grupa zapomina o istnieniu wszystkich pozostałych alokacji. Ważne jest tylko to kto z uczestników preferuje x a kto y. Aksjomat ten formalizujemy następująco: niech (≥_i) i (→_i) to dwie rodziny indywidualnych preferencji, 1≤ i ≤ n₁; połóżmy ≥_s =P (≥ _1, ≥_2, …≥_m) oraz →_s = P (→_1, →_{2 ,}→_m), niech x i y to są dowolne dwie dopuszczalne alokacje ”R” wtedy (x ≥_i y dla każdego i wtedy i tylko wtedy, gdy x →_i y) wtedy i tylko wtedy, gdy ( x ≥_s y wtedy i tylko wtedy, gdy x →_s y)

6. P nie jest prawem dyktatora

Warunki 1,2,3,4,5 i 6 nie mogą zachodzić jednocześnie tzn. zajście dowolnych 5 z nich implikuje, że pozostały warunek nie zachodzi. Powyższe implikacje oznaczają twierdzenie - jeśli dana relacja grupowej preferencji spełniająca aksjomat jednomyślności i niezależności to jest ona dyktaturą tzn. pokrywa się z relacją preferencji któregoś z uczestników klubu.

9. Sformułuj twierdzenie o istnieniu wektora cen równowagi Debrewn i wyjaśnij pojęcia występujące w tym stwierdzeniu.

Założenia:

P = (P_1,P_2,….P_i) € R^l - wektor cen

∏ - obszar cen

H1 - dla każdego 1 ≤ i ≤ m funkcja użyteczności n_i zależy tylko od x^l € R

H2 - Ω = Ω¹ + Ω² +…. Ω^m (całkowite zasoby towarów)

H3 - dla każdego 1 ≤ i ≤ m relacja preferencji ≥ _i jest ciągła, monotoniczna i ściśle wypukła.

Załóżmy, że są spełnione założenia H1, H2, H3 oraz, że dla każdego 1 ≤ i ≤ l Ω _kⁱ (omega)≠ 0, wtedy istnieje p € ∏ wtedy (P)=0. Prawdziwe jest następujące twierdzenie, jeśli spełnione są założenia H1, H2 i H3 to istnieje wektor cen równowagi.

Założenie, że dla każdego i oraz k Ω _kⁱ jest różne od zera jest założeniem technicznym ułatwiającym dowód twierdzenia. Twierdzenie to jest prawdziwe bez tego założenia.

Równość popytu i podaży na całym rynku wyraża się za pomocą równania wektorowego: z(p)=0.

Alokacja równowagi -,mówimy, że wektor cen p należący do ∏ jest wektorem cen równowagi jeśli z(p) jest równe wektorowi zerowemu z(p)=0.Odpowiadającą mu alokację (d¹(p), d²(p) …d^m(p)) nazywamy alokacją równowagi.

1

---