Wydział Inżynierii Środowiska

Semestr I

Grupa II

Wyznaczanie pojemności kondensatora z krzywej rozładowania

1. Wstęp Teoretyczny

Kondensator - jest to układ dwóch przewodników przedzielonych izolatorem.

Pojemność kondensatora jest to stosunek ładunku zgromadzonego na przewodniku do wywołanego przez ten ładunek potencjału:

Każdy przewodnik ma pewną zdolność gromadzenia ładunków elektrycznych, która jest zależna zarówno od samego przewodnika, jak i od jego otoczenia. Aby móc precyzyjnie ją określić, posługujemy się pojęciem pojemności elektrycznej.

Pojemnością elektryczną przewodnika nazywamy stosunek ładunku zgromadzonego na przewodniku do wywołanego przez ten ładunek potencjału. Pojemność elektryczna jest wielkością informującą nas, ile ładunku należy wprowadzić na przewodnik, aby uzyskać potencjał równy jednostce.

Jednostką pojemności jest farad (1F). Jednostką pojemności elektrycznej w układzie SI jest farad ().

Przewodnik ma pojemność jednego farada, gdy ładunek jednego Culomba wywołuje na nim potencjał jednego wolta. Ponieważ jest to jednostka zbyt duża do celów praktycznych, zwykle posługujemy się jednostkami mniejszymi:

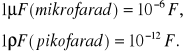
Pojemność przewodnika zależy od rodzaju otaczającego go środowiska.

Taką pojemność posiada przewodnik, którego potencjał wzrasta o 1V przy dostarczaniu mu ładunku 1C. Pojemność przewodnika zależy od jego rozmiarów oraz kształtu i jest taka sama niezależnie od tego, czy jest on naładowany, czy nie.

Definiując pojemność zakładamy, że w pobliżu przewodnika nie ma innych przewodników

i ciał naładowanych. Doświadczenia pokazują, że umieszczając w pobliżu przewodnika drugi przewodnik, uziemiony lub naładowany przeciwnie, zwiększamy jego pojemność. Taki układ przewodników, w którym obecność jednego wpływa na pojemność drugiego przewodnika nazywamy kondensatorem. Tworząc go przewodniki nazywamy okładkami kondensatora.

W najprostszym kondensatorze (kondensator płaski) są to dwie równoległe płyty odsunięte nieco od siebie. Między płytami kondensatora płaskiego, którego okładki naładowane są różnoimiennie istnieje jednorodne pole elektrostatyczne.

Pojemność kondensatora, między płytkami którego znajduje się powietrze, rośnie wraz ze wzrostem powierzchni okładek i maleje ze wzrostem ich odległości.

Prąd rozładowania I kondensatora przez opór R zmienia się według równania:

Z definicji natężenia prądu
, skąd ładunek zgromadzony na okładkach kondensatora można wyznaczyć całką
. W sensie geometrycznym całka ta równa jest polu pod wykresem I(t).

2. Przebieg Ćwiczenia

1. Podłączyć układ według schematu.

2. Wyliczyć wartość oporu, dla ustalonego napięcia.

3. Ustawić opornicę dekadową na R_Z.

4. Zamknąć wyłącznik K i dopasować oporność R opornicy dekadowej do wartości, by uzyskać pełne wychylenie 300μA.

5. Podzielić przedział prądowy.

6. Naładować kondensator C przez zwarcie wyłącznika K. Zmierzyć czas od chwili zwolnienia wyłącznika K do chwili, gdy wskazówka przyrządu mija I_1.

7. Czynność jak wyżej powtórzyć dla kolejnych wartości K. Wyniki wpisać do tabeli.

8. Zapisać dane przyrządów pomiarowych oraz błędy

9. Obliczyć średnie czasy i sporządzić wykres prądu rozładowania jako funkcji czasu.

10. Obliczyć pole powierzchni zawartej pod wykresem.

11. Wyznaczyć stałą wykresu
[C/mm²]

12. Obliczyć ładunek kondensatora
[C]

13. Obliczyć pojemność kondensatora
[F]

14. Obliczyć błędy metodą różniczkowania logarytmu naturalnego

15. Metodą wyrównawczą Gaussa wyznaczyć wykładnik
funkcji oraz błąd tego wykładnika
(za pomocą komputera).

16. Obliczyć pojemność kondensatora

17. Obliczyć błąd pojemności

18. Zestawić wyniki uzyskane obiema metodami

3. Obliczenia:

-Obliczamy średnie czasy:

(wyniki wpisane są w tabeli)

i na papierze milimetrowym sporządzamy wykres prądu rozładowania jako funkcji czasu I(t).

- Wyznaczamy stałą wykresu:

[C/mm
]

dla I

dla t

3. Wyznaczamy pole powierzchni zawartej pod wykresem:

Pole powierzchni zawartej pod wykresem zostało obliczone. Do obliczeń powierzchnię podzielono na prostokąty i trójkąty:

Pole powierzchni zawartej pod wykresem S = 4920 [mm²]

4.Obliczamy pojemność kondensatora:

Aby obliczyć pojemność kondensatora potrzebujemy q(ładunek kondensatora), aby go obliczyć korzystamy z wzoru:

q = S·α

q = 4920 · 1·10^-6

Obliczamy błąd pojemności metodą różniczkowania logarytmu naturalnego:

gdzie:

stąd:

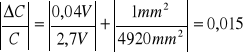
Błąd względny:

Metodą wyrównawczą Gaussa wyznaczamy wykładnik
oraz błąd tego wykładnika(przy pomocy komputera)

• do komputera wprowadzamy następujące dane:

x₁- 1,07 y₁- 280 x₆- 7,4 y₆- 180

x₂- 2,2 y₂- 260 x₇- 9,3 y₇- 160

x₃- 3,33 y₃- 240 x8- 11,2 y₈- 140

x₄- 4,87 y₄- 220 x₉- 13,4 y₉- 120

x₅- 6,0 y₅- 200 x₁₀- 16,2 y₁₀- 100

x₁₁- 19,6 y₁₁- 80

x₁₂- 24,0 y₁₂-60

x₁₃- 29,7 y₁₃- 40

x₁₄- 40,1 y₁₄- 20

otrzymaliśmy następujące parametry:

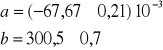
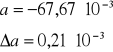
Obliczamy pojemność kondensatora:

Błąd bezwzględny:

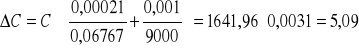
Błąd względny:

Zestawienie wyników:

Metoda całkowania graficznego

Metoda wyrównawcza Gaussa

5.Wnioski

Zadaniem ćwiczenia było wyznaczenie pojemności kondensatora z krzywej rozładowania. Błędy obliczeń wynikają z niedokładności przyrządów pomiarowych, niedokładności obserwatora i błędów wykonanych obliczeń.

Pojemność kondensatora obliczana metodą całkowania graficznego wynosi
, błąd mierzenia pojemności wynosi 1,5%.

Pojemność kondensatora obliczana metodą wyrównawczą Gaussa wynosi
, błąd wynosi 0,31%.

---