MIERNICTWO CYFROWE
ZADANIA: Cyfrowe pomiary częstotliwości i czasu
NAZWISKO:	OCENA:
GRUPA:

Praca zawiera:

1. Podział błędów 2

2. Rachunek błędów 3

3. Cele przeprowadzania ćwiczenia 4

4. Zastosowane przyrządy pomiarowe 4

5. Przebieg ćwiczenia i opracowanie wyników 4

6. Wnioski 12

1. Podział błędów

Wykonanie każdego pomiaru wielkości fizycznej obarczone jest błędem, błędy te wynikać mogą z szeregu przyczyn zarówno powodowanych przez człowieka, przyrząd pomiarowy lub też sam obiekt pomiarowy. W związku czym aby poprawnie opracować wyniki pomiaru konieczne jest określenie jego błędu. W momencie gdy nie potrafimy go określić wyniki naszego pomiaru stają się bezużyteczne gdyż nie wiemy w jakim stopniu są one obarczone błędami. W procesie pomiaru można wyróżnić trzy etapy:

• wyznaczenie szukanej wielkości fizycznej,

• określenie błędu pomiaru,

• podanie przypuszczalnych przyczyn błędów.

Ogólnie błędy pomiarowe podzielić możemy na :

• błędy grube (nadmiarowe) wynikłe z nieuwagi i z pomyłek osoby (grupy osób) przeprowadzającej pomiary ( np. przy odczycie lub w zapisie wyniku). Często są jednorazowe i mogą być bardzo duże.

• błędy systematyczne wynikłe ze złego (mało dokładnego) ustawienia samego przyrządów pomiarowych ich, ze stanu zewnętrznych warunków pomiaru jak i z błędu osoby (grupy osób) przeprowadzającej pomiary (np. znany błąd paralaksy). Błąd systematyczny charakteryzuje się stałą lub zmieniającą się według określonego prawa odchyłką wartości wyznaczanej w doświadczeniu w porównaniu z wielkością rzeczywistą. Przyczyny błędów systematycznych mogą być poznane i usunięte.

• błędy przypadkowe wynikłe z niedokładności odczytu, zmiany warunków pomiaru, z nieokreślenia samej mierzonej wielkości fizycznej itd. Błędy te odznaczają się tym, że w serii pomiarów jednego i tego samego stanu danej wielkości fizycznej wykonywanej w określonych warunkach, wyniki zmieniają się w sposób losowy (przypadkowy). Nie można ich uniknąć (usunąć), gdyż nie znamy ich przyczyn. Nie można więc wykonać bezbłędnego wyznaczenia wielkości fizycznej - pomiaru absolutnie dokładnego.

Błędy pomiarowe podzielić możemy również ze względu na źródła ich powstania, rozróżniamy w takim podziale następujące rodzaje błędów pomiarowych:

• błędy powodowane przez przyrządy pomiarowe, np. bezwładność, próg czułości przyrządów pomiarowych, ich nieliniowiść lub niedoskonałość ich wzorcowania,

• błędy powodowane przez metody pomiarowe,

• błędy powodowane przez mierzącego, np. brak doświadczenia, skłonności, zmęczenie, nawyki,

• błędy powodowane przez obliczenia - błędy przy niewłaściwym zaokrągleniu, niewłaściwe metody wyrównywania błędów,

• błędy powodowane przez wpływ otoczenia na mierzącego, na przyrządy i na mierzoną wielkość.

Czynniki wywołujące te błędy głównie czynniki zewnętrzne działające na układ pomiarowy możemy do nich zaliczyć np. temperaturę, ciśnienie, wilgotność powietrza, zakłócenia

elektromagnetyczne.

2. Rachunek błędów.

Powstałe podczas pomiaru błędy sklasyfikować możemy podczas obliczeń do kilku podstawowych rodzajów różniących się zastosowaniem, sposobem wyliczanie oraz sposobem prezentacji:

• Błąd bezwzględny - jest różnicą między wynikiem pomiaru x a wartością prawdziwą (rzeczywistą) wielkości mierzonej x­_r, czyli:

∆=x-x_r

Błąd bezwzględny, zawsze wyrażony w jednostkach wielkości marzonej, ma konkretny znak: plus (+) lub minus (-).

• Błąd względny - jest to stosunek błędu bezwzględnego pomiaru do wartości rzeczywistej wielkości mierzonej:

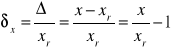
Błąd względny jest zwykle podawany w procentach.

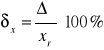
• Poprawka - jest to błąd bezwzględny z przeciwnym znakiem.

Dodając algebraicznie poprawkę p do wartości x uzyskanej z pomiarów, otrzymuje się wynik poprawiony, równy wartości poprawnej.

x_p=x+p

Jednakże praktyczną miarą niedokładności pomiarów są jednak graniczne błędy pomiarów określane jako najmniejszy przedział wokół zmierzonych wartości X, wewnątrz którego znajduje się wartość rzeczywista x_r.

lub

Nierówności te zapisujemy graficznie w postaci:
lub

2. Cele przeprowadzania ćwiczenia

Głównym celem ćwiczenia było zapoznanie się z metodami pomiarów częstotliwości i czasu oraz przyrządami pomiarowymi potrzebnymi do zrealizowania ćwiczenia, ja również z metodami obliczania błędów pomiarów.

4. Zastosowane przyrządy pomiarowe

Do generacji wzorcowego sygnału użyliśmy generatora PF 1641A, przebiegi sygnału mierzyliśmy oscyloskopem cyfrowym OS-310M oraz częstościomierzem cyfrowym PFL-28A.

5. Przebieg ćwiczenia i opracowanie wyników

Naszym pierwszym zadaniem było zapoznanie się instrukcjami obsługi poszczególnych przyrządów potrzebnych do przeprowadzenia zadania.

Kolejnym krokiem było połączenie przyrządów pomiarowych wg następującego schematu:

Po połączeniu urządzeń przystąpiliśmy do przeprowadzania pomiarów. Pomiary przeprowadzaliśmy w 4 etapach:

1. 10 pomiarów częstotliwości od 0 Hz do 10 Hz ze skokiem około 1 Hz

2. 9 pomiarów częstotliwości od 20 Hz do 100 Hz ze skokiem około 10 Hz

3. 9 pomiarów częstotliwości od 200 Hz do 1000 Hz ze skokiem około 100 Hz

4. 9 pomiarów częstotliwości od 1000 Hz do 10 000 Hz ze skokiem około 1 000 Hz

W sumie przeprowadziliśmy 37 pomiarów. Z każdego pomiaru notowaliśmy na kartce wskazania wszystkich 3 przyrządów.

Dzięki możliwościom jakie daje oscyloskop cyfrowy wyniki zanotowaliśmy zarówno okres jak i częstotliwość mierzonego sygnału co ułatwiło nam dalsze obliczenia błędów pomiarowych ponieważ zamieniliśmy na częstotliwość wyłącznie wskazania generowane przez wzorzec.

Podczas przeprowadzania ćwiczenie dbaliśmy o dokładność pomiarów, staraliśmy się ustawiać przyrządy pomiarowe tak aby jak najdokładniej wyznaczyć punkty, w których mieliśmy zanotować wyniki pomiarów.

Podczas opracowywania wyników pomiarów za wzorzec (wartość rzeczywistą) przyjęliśmy wyniki wskazań częstościomierza cyfrowego PFL-28A.

LP	Wzorzec [ms]	oscyloskop	jm	Generator [Hz]	Wzorzec [Hz]	błąd bezwzględny wzorzec -oscyloskop [Hz]	błąd bezwzględny wzorzec -generator [Hz]	błąd względy wzorzec -oscyloskop [%]	błąd względy wzorzec -generator [%]
1	955,680	952,000	ms	1,050	1,0464	0,0036	0,0036	0,34640%	0,3464%
										1,050	Hz
		2	501,600							496,000	ms	2,000	1,9936	0,1064	0,0064	5,33600%	0,3200%
										2,100	Hz
		3	330,880							344,000	ms	3,020	3,0222	-0,1162	-0,0022	-3,84627%	-0,0742%
										2,906	Hz
		4	246,220							244,000	ms	4,050	4,0614	0,0366	-0,0114	0,90096%	-0,2809%
										4,098	Hz
		5	199,520							200,000	ms	5,000	5,0120	-0,0120	-0,0120	-0,24000%	-0,2400%
										5,000	Hz
		6	166,080							168,000	ms	6,010	6,0212	-0,0692	-0,0112	-1,14918%	-0,1859%
										5,952	Hz
		7	143,100							142,400	ms	6,980	6,9881	0,0339	-0,0081	0,48482%	-0,1162%
										7,022	Hz
		8	124,130							124,800	ms	8,050	8,0561	-0,0441	-0,0061	-0,54704%	-0,0753%
										8,012	Hz
		9	111,060							112,000	ms	8,990	9,0041	-0,0761	-0,0141	-0,84563%	-0,1571%
										8,928	Hz
		10	100,060							100,000	ms	9,990	9,9940	0,0060	-0,0040	0,06000%	-0,0401%
										10,000	Hz
		11	48,760							48,790	ms	20,050	20,5086	-0,0186	-0,4586	-0,09076%	-2,2362%
										20,490	Hz
		12	33,050							33,200	ms	30,020	30,2572	-0,1372	-0,2372	-0,45340%	-0,7839%
										30,120	Hz
		13	24,780							24,600	ms	40,030	40,3551	0,2949	-0,3251	0,73070%	-0,8057%
										40,650	Hz
		14	20,000							20,000	ms	49,900	50,0000	0,0000	-0,1000	0,00000%	-0,2000%
										50,000	Hz
LP	Wzorzec [ms]	oscyloskop	jm	Generator [Hz]	Wzorzec [Hz]	błąd bezwzględny wzorzec -oscyloskop [Hz]	błąd bezwzględny wzorzec -generator [Hz]	błąd względy wzorzec -oscyloskop [%]	błąd względy wzorzec -generator [%]
15	16,650	17,000	ms	60,000	60,0601	-1,2401	-0,0601	-2,06470%	-0,1000%
										58,820	Hz
		16	14,290							14,400	ms	69,800	69,9790	-0,5390	-0,1790	-0,77024%	-0,2558%
										69,440	Hz
		17	12,510							12,560	ms	79,700	79,9361	-0,3261	-0,2361	-0,40789%	-0,2953%
										79,610	Hz
		18	11,040							11,120	ms	90,400	90,5797	-0,6597	-0,1797	-0,72832%	-0,1984%
										89,920	Hz
		19	10,030							10,000	ms	99,600	99,7009	0,2991	-0,1009	0,30000%	-0,1012%
										100,000	Hz
		20	5,026							5,000	ms	198,400	198,9654	1,0346	-0,5654	0,52000%	-0,2842%
										200,000	Hz
		21	3,336							3,300	ms	299,700	299,7602	3,2398	-0,0602	1,08080%	-0,0201%
										303,000	Hz
		22	2,503							2,500	ms	399,900	399,5206	0,4794	0,3794	0,12000%	0,0950%
										400,000	Hz
		23	1,999							2,000	ms	499,500	500,2501	-0,2501	-0,7501	-0,05000%	-0,1499%
										500,000	Hz
		24	1,667							1,664	ms	599,900	599,8800	1,0200	0,0200	0,17003%	0,0033%
										600,900	Hz
		25	1,428							1,424	ms	700,300	700,2801	1,9199	0,0199	0,27416%	0,0028%
										702,200	Hz
		26	1,249							1,248	ms	800,900	800,6405	0,5595	0,2595	0,06988%	0,0324%
										801,200	Hz
		27	1,111							1,112	ms	900,900	900,0900	-0,8900	0,8100	-0,09888%	0,0900%
										899,200	Hz
		28	0,998							1,000	ms	1 003,000	1 002,0040	-2,0040	0,9960	-0,20000%	0,0994%
										1 000,000	Hz
LP	Wzorzec [ms]	oscyloskop	jm	Generator [Hz]	Wzorzec [Hz]	błąd bezwzględny wzorzec -oscyloskop [Hz]	błąd bezwzględny wzorzec -generator [Hz]	błąd względy wzorzec -oscyloskop [%]	błąd względy wzorzec -generator [%]
29	0,5018	0,5000	ms	1 999,000	1 992,8258	7,1742	6,1742	0,36000%	0,3098%
										2 000,0000	Hz
		30	0,3337							0,3340	ms	3 007,000	2 996,7036	-2,7036	10,2964	-0,09022%	0,3436%
										2 994,0000	Hz
		31	0,2505							0,2520	ms	4 000,000	3 992,0160	-24,0160	7,9840	-0,60160%	0,2000%
										3 968,0000	Hz
		32	0,2003							0,2000	ms	4 997,000	4 992,5112	7,4888	4,4888	0,15000%	0,0899%
										5 000,0000	Hz
		33	0,1666							0,1664	ms	6 005,000	6 002,4010	6,5990	2,5990	0,10994%	0,0433%
										6 009,0000	Hz
		34	0,1430							0,1440	ms	7 000,000	6 993,0070	-49,0070	6,9930	-0,70080%	0,1000%
										6 944,0000	Hz
		35	0,1251							0,1255	ms	8 000,000	7 993,6051	-32,6051	6,3949	-0,40789%	0,0800%
										7 961,0000	Hz
		36	0,1110							0,1120	ms	9 005,000	9 009,0090	-81,0090	-4,0090	-0,89920%	-0,0445%
										8 928,0000	Hz
		37	0,0996							0,1015	ms	10 040,000	10 040,1606	-198,1606	-0,1606	-1,97368%	-0,0016%
										9 842,0000	Hz

Wykres 1. Wymiar błędu bezwzględnego oscyloskopu cyfrowego

Wykres 2. Wymiar błędu bezwzględnego generatora

Wykres 3. Wymiar błędu względnego oscyloskopu cyfrowego

Wykres 4. Wymiar błędu względnego generatora

Wykres 5. Wymiar wartości bezwzględnej błędu względnego generatora oraz oscyloskopu

Wykres 6. Wymiar wartości bezwzględnej błędu bezwzględnego generatora oraz oscyloskopu

7. Wnioski

Wykresy 1. oraz 2 przedstawiają wartości błędu bezwzględnego w funkcji częstotliwości dla oscyloskopu oraz generatora.

Z wykresów tych możemy stwierdzić iż błąd względny rośnie wraz ze wzrostem częstotliwości dla obu tych przyrządów. Jednakże dokładniejszym przyrządem okazuje tu się generator jego maksymalny błąd wynosi 10,2964 Hz i jest o ponad 19 razy mniejszy od maksymalnego błędu oscyloskopu. Dokładniej wymiary błędu bezwzględnego dla obu przyrządów porównać możemy na wykresie 6. Przedstawione na nim są wartości bezwzględne tegoż błędu w funkcji częstotliwości. Wykres ten daje nam obraz na różnice w dokładności obu przyrządów, wynika z niego jednoznacznie że dokładniejszym przyrządem jest generator.

Wykresy 3 oraz 4 przedstawiają wartości błędu względnego w funkcji częstotliwości zarówno dla oscyloskopu (wykres 3) jak i generatora (wykres 4).

Po przeanalizowaniu wykresów również stwierdziliśmy że mniej dokładnym przyrządem okazał się być oscyloskop. Stworzenie wykresu 5 przedstawiającego wartość bezwzględna tego błędu (wyrażoną w procentach) w funkcji częstotliwości podyktowane było chęcią dokładnego zweryfikowania powyższego twierdzenia, wynika z niego jednoznacznie że oscyloskop przejawiał większe błędy względne niż generator.

Podczas opracowywania wyników stwierdziliśmy że wartości błędów bezwzględnych rosną ze zwiększającą się częstotliwością. Wartości tego błędu zaczynają lawinowo rosnąć po przekroczeniu progu 1 000 Hz. Przy mniejszych częstotliwościach błędy te SA znikome i mieszczą się w granicach 2 Hz. Natomiast po przekroczeniu granicy 1 000 Hz maksymalny błąd bezwzględny jaki odnotowaliśmy to -198,1606 Hz.

Jednakże podczas opracowywania błędów względnych zauważyliśmy że maksymalny błąd względny wyniósł 5,336% dla oscyloskopu a dla generatora -2,2362%. Co świadczy o dokładności przyrządów. Jednakże maksymalny błąd oscyloskopu względny wystąpił dla małej wartości częstotliwości co sugeruje popełnienie błędu podczas przeprowadzania pomiarów. Jednakże z całości przebiegu przedstawionego na wykresie 5 stwierdzić możemy jednoznacznie ze generator jest przyrządem o wiele dokładniejszym od oscyloskopu.

OSCYLOSKOP

---