I EF-ZI 15.01.2012r
Laboratorium z fizyki
Ćw. nr: 2
Wyznaczanie prędkości lotu pocisku na podstawie badania ruchu wahadła balistycznego
XXXX XXXX
L 4
Wstęp teoretyczny.
Ruch obrotowy bryły sztywnej to taki ruch, w którym wszystkie punkty bryły poruszają się po okręgach o środkach leżących na jednej prostej zwanej osią obrotu. Np. ruch Ziemi wokół własnej osi. Jest to ruch złożony z ruchu postępowego środka masy danego ciała oraz ruchu obrotowego względem pewnej osi. Środek masy ciała można uważać za punkt materialny. Do opisania ruchu obrotowego używa się odmiennych pojęć od używanych do opisania ruchu postępowego.
Podstawowym prawem opisującym ruch bryły sztywnej jest druga zasada dynamiki ruchu obrotowego:
gdzie
gdzie M jest momentem siły względem obranego punktu odniesienia, a L - krętem (momentem pędu) względem tego samego punktu odniesienia.
Jeżeli obrót odbywa się względem osi stałej lub sztywnej wówczas druga zasada dynamiki dla ruchu obrotowego może być napisana w następujący sposób:
gdzie M oznacza moment siły a I moment bezwładności względem osi obrotu.
Gdy brak momentu sił zewnętrznych (M = 0), z pierwszego wzoru można otrzymać równanie ilustrujące zasadę zachowania momentu pędu
Gdy oś obrotu jest ustalona, brak momentu sił oznacza stałość prędkości kątowej, ponieważ
co przy stałości I oznacza
b) Drgania harmoniczne proste odbywają się pod wpływem działania siły zwracającej:
F = - k * x
x - wychylenie z położenia równowagi
k - współczynnik proporcjonalności
„ - ” - oznacza, że siła jest skierowana przeciwnie do wychylenia.
Zgodnie z II zasadą dynamiki drgania te opisuje równanie:
![]()
m - masa ciała wykonującego drgania
Wahadło fizyczne.
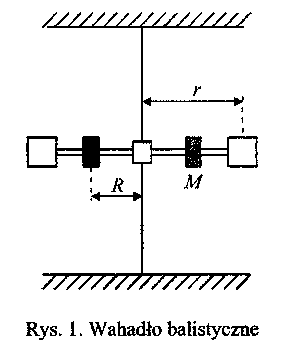
Przykładem oscylatora harmonicznego jest wahadło fizyczne, czyli bryła sztywna mogąca obracać się wokół osi nie przechodzącej przez środek masy.
m - masa wahadła
c - środek ciężkości
![]()
- kąt odchylenia wahadła od pionu![]()
W wyniku odchylenia wahadła z położenia równowagi o kąt ![]()
powstaje moment obrotowy, który stara się zawrócić wahadło do położenia równowagi.
![]()
l - odległość od osi obrotu do środka ciężkości.
Tabela pomiarowa
R1 |
t1 |
R2 |
t2 |
αmax |
r |
m |
M |
D |
I0 |
v |
u(v) |
[m] |
[s] |
[m] |
[s] |
[rad] |
[m] |
[kg] |
[kg] |
[Nm] |
[kgm2] |
[m/s] |
[m/s] |
0.02 |
10.951 |
0.09 |
17.937 |
αmax1= |
0.115 |
0.0064 |
0.194 |
0.019 |
0.0016 |
26.2 |
0.0044 |
|
10.946 |
|
17.943 |
|
|
|
|
|
|
|
|
|
10.942 |
|
17.842 |
|
|
|
|
|
|
|
|
|
10.947 |
|
17.923 |
|
|
|
|
|
|
|
|
|
10.946 |
|
17.931 |
|
|
|
|
|
|
|
|
|
10.937 |
|
17.914 |
αmax2= |
|
|
|
|
|
25.2 |
|
|
10.936 |
|
17.940 |
|
|
|
|
|
|
|
|
|
10.942 |
|
17.890 |
|
|
|
|
|
|
|
|
|
10.942 |
|
17.928 |
|
|
|
|
|
|
|
|
|
10.942 |
|
17.932 |
|
|
|
|
|
|
|
|
Obliczenia
∆m = ![]()
0,001g = ![]()
0,000001 kg
∆αmax = ![]()
10 = ![]()
0,017 rad
∆R1 = ∆R2 = ![]()
1mm = ![]()
0,001m
∆r = ![]()
1mm = ![]()
0,001m
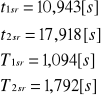
Obliczanie momentu kierującego D sprężyny oraz stałą część momentu bezwładności wahadła I0:
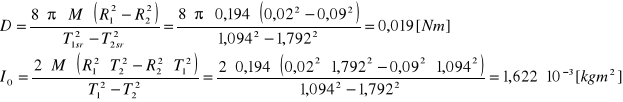
Obliczanie prędkości V pocisku:
![]()
![]()
Obliczanie niepewności standardowych u(t1śr) i u(t2śr) metodą typu A:
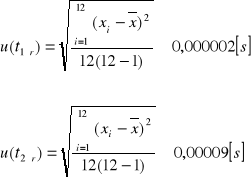
Obliczanie niepewności standardowych u(T1śr) i u(T2śr) z prawa przenoszenia niepewności:
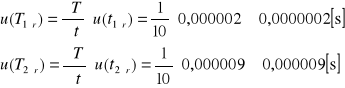
Obliczyć niepewności standardowe u(R1) i u(R2) metodą typu B:
![]()
Obliczanie niepewności standardowych u(D) i u(I0) z prawa przenoszenia niepewności:

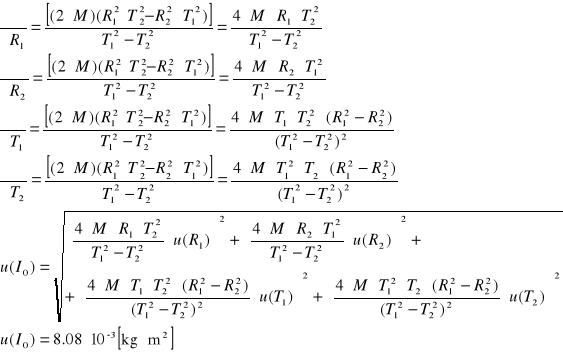
Obliczanie niepewności standardowych u(αmax), u(r) i u(m) metodą typu B:
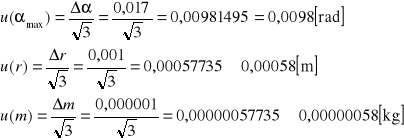
Obliczanie niepewności standardowej prędkości pocisku u(V) z prawa przenoszenia niepewności:
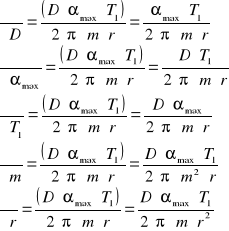
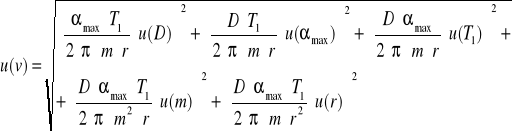
![]()
![]()
Wyniki:
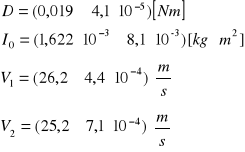
Wnioski:
Można zauważyć, że wraz ze zwiększeniem się prędkości pocisku zwiększa się wychylenie się wahadła. Prędkość pocisku nie zależy od momentu kierującego wahadła, kąta wychylenia lub trwania okresu drgań. Zależy natomiast od masy pocisku.
Wyszukiwarka
Podobne podstrony:
Spr27, Politechnika Rzeszowska, Fizyka Sprawozdania, Cw27
29 sprawozdanie, Politechnika Rzeszowska, Fizyka Sprawozdania, prz inf 2011
9 Cw. II zasady dynamiki Newtona dla ruchu obrotowego bry+é, Politechnika Rzeszowska, Fizyka, Sprawo
cw.27, Politechnika Rzeszowska, Fizyka, Sprawozdania
cw32, Politechnika Rzeszowska, Fizyka Sprawozdania, Cw32
Ćw 4 Fizyka, Politechnika Rzeszowska, Fizyka Sprawozdania, prz inf 2011
SPRAWOZDANIE 45, Politechnika Rzeszowska, Fizyka Sprawozdania, prz inf 2011
Laboratorium fizyka ćw 1A, Budownictwo Politechnika Rzeszowska, Fizyka, Moje zaliczone sprawozdania
W2(1), Politechnika Łódzka, fizyka-sprawozdania
ćw.2 spr2, Politechnika Rzeszowska, Chemia
54+, Politechnika Rzeszowska, Elektrotechnika, semestr 2, Fizyka Lab, Sprawozdania, Fizyka Laborator
sprawozdanie 01 nowe, Politechnika Rzeszowska Budownictwo, IBD, Fizyka
1B+, Politechnika Rzeszowska, Elektrotechnika, semestr 2, Fizyka Lab, Sprawozdania, Fizyka Laborator
pierwsza str fiz, Politechnika Rzeszowska Budownictwo, IBD, Fizyka, sprawozdanie
pierwsza str teczki fiz, Politechnika Rzeszowska Budownictwo, IBD, Fizyka, sprawozdanie
44 sprawozdanie czyjeś, Politechnika Rzeszowska, Elektrotechnika, semestr 2, Fizyka Lab, Sprawozdani
więcej podobnych podstron