I EF-ZI 29.01.2012r

Laboratorium z fizyki

Ćw. nr: 27

Wyznaczanie indukcyjności cewki i pojemności kondensatora
w obwodzie prądu zmiennego

Artur Solarz

L 4

I. Wstęp teoretyczny

Prąd elektryczny jest to zjawisko fizyczne wywołane uporządkowanym ruchem ładunków elektrycznych przez badany przekrój poprzeczny danego ośrodka. Przepływ prądu elektrycznego wywołuje zjawiska: magnetyczne, cieplne, chemiczne, mechaniczne, świetlne i inne za pośrednictwem których poznaje się istnienie prądu elektrycznego.

Rozróżnia się m. in. prąd elektryczny:

• stały - prąd jednokierunkowy , którego natężenie nie ulega zmianie w funkcji czasu

• zmienny - w funkcji czasu zmienia się natężenie lub zwrot.

Jeśli w przypadku prądu zmiennego zmiany zachodzą okresowo , to prąd taki nazywa się przemiennym , a wartość średnia całookresowa natężenia prądu równa się zeru.

i _śr (t) = (1/ T) ∫ i(t )dt = 0

gdzie: T - okres zmian prądu - czas , w którym prąd wykonuje jeden cykl zmian.

Najprostszym i najczęściej spotykanym prądem elektrycznym przemiennym jest prąd sinusoidalny, którego przebieg jest sinusoidalną funkcją czasu.

i(t) = Im sin(ωt + ϕ)

gdzie: i(t) - wartość chwilowa natężenia prądu.

I_m - amplituda wielkości sinusoidalnej (wartość szczytowa prądu).

ω - pulsacja (częstość kątowa) ω = 2πf ; f - częstotliwość

ϕ - faza początkowa (początkowy kąt fazowy) - wielkość ta pozwala określić wartość prądu w chwili początkowej , tj. w chwili od której rozpoczęto rozpatrywać przebieg danej wielkości.

Prąd przemienny charakteryzują również takie wielkości jak wartość średnia prądu oraz wartość skuteczna.

Wartość skuteczną określa poniższy wzór:

I_SK = √ (1/T) ∫ i² (t)dt

Interpretacja fizyczna wartości skutecznej prądu przemiennego jest następująca::

Wartość skuteczna natężenia prądu, jest to wartość liczbowo równa takiej wartości prądu stałego, który w tym samym czasie i na tym samym oporze wydzieli taką samą ilość ciepła.

Wartość średnia całookresowa prądu przemiennego jest równa zero, dlatego podaje się wartość średnią półokresową. Wartość tę można policzyć ze wzoru:

I_ŚR = (1/T) ₀∫^T i(t)dt

Wartość średnia półokresowa prądu przemiennego jest równa takiej ilości prądu stałego który w tym samym czasie (połowie okresu) przeniesie taki sam ładunek co dany prąd przemienny.

Elementy R, L, C. Rozpatrując obwody prądu elektrycznego, możemy wyróżnić następujące elementy tych obwodów : odbiorniki o oporności czynnej (rezystancji) i biernej (reaktancji). Do pierwszej grupy zaliczamy m. in. rezystory (R - rezystancja), do drugiej zaś cewki (L - indukcyjność) i kondensatory (C - pojemność).

Odbiornik o oporności czynnej to takie odbiorniki których indukcyjność oraz pojemność jest znikomo mała i można ją pominąć.

Prąd przepływający przez taki odbiornik wyrazi równanie:

i = I_m sin ωt

Spadek napięcia u na oporności czynnej R przy jej niezmiennej wartości jest tym większy, im większa jest wartość przepływającego prądu, więc chwilowe napięcie jest największe (U_m) w chwili, gdy wartość chwilowa przepływającego prądu i jest szczytowa (I_m). Gdy prąd i = 0 , to napięcie u = 0. Napięcie i prąd na rezystancji są zgodne w fazie, osiągają w tych samych momentach swe wartości szczytowe dodatnie i ujemne oraz zerowe

Gdy przez cewkę lub kondensator płynie prąd przemienny, wtedy część energii magazynowana jest w polu, odpowiednio magnetycznym lub elektrycznym. Wywołuje to spadek napięcia wprost proporcjonalny do iloczynu prądu i reaktancji. W przypadku obwodów prądu stałego nie mówi się o reaktancji, bowiem cewka stanowi zwarcie, zaś kondensator przerwę w obwodzie.

Reaktancja idealnej cewki i kondensatora jest równa co do wartości bezwzględnej ich impedancji. Napięcie i prąd w takich elementach są przesunięte w fazie o 90 stopni względem siebie. Znak liczby zależy od tego, czy prąd wyprzedza napięcie, czy napięcie wyprzedza w fazie prąd.

Reaktancja cewki (opór indukcyjny, induktancja) ma znak dodatni i oblicza się ją ze wzoru:

gdzie L to indukcyjność własna cewki,
- pulsacja.

Reaktancja kondensatora (opór pojemnościowy, kapacytancja) oblicza się ją ze wzoru:

gdzie: C - pojemność kondensatora,
- pulsacja.

We wzorze na reaktancję składowa indukcyjna występuje ze znakiem dodatnim, a pojemnościowa - z ujemnym:

Wykresy wektorowe obwodu

W przypadku analizy obwodów RLC w stanie ustalonym ważnym pojęciem jest wykres wektorowy, zwany również wykresem wskazowym, przedstawiający w sposób orientacyjny zależności między poszczególnymi wektorami prądu i napięcia w obwodzie. Jak wiadomo każdej liczbie zespolonej można przyporządkować reprezentację geometryczną w postaci odpowiedniej zależności wektorowej przedstawionej na płaszczyźnie, w której oś pozioma odpowiada części rzeczywistej a oś pionowa części urojonej liczby zespolonej. Konstruując wykres należy pamiętać, że pomnożenie wektora przez operator
jest równoważne jego obrotowi o kąt 90 stopni przeciwnie do ruchu wskazówek zegara gdyż operator j jest równy
Podobnie pomnożenie wektora przez operator
jest równoważne jego obrotowi o kąt 90 stopni zgodnie z ruchem wskazówek zegara gdyż operator -j jest równy
Pomnożenie wektora przez liczbę rzeczywistą nie zmienia pozycji wektora w przestrzeni o ile jest to liczba dodatnia lub zmienia zwrot wektora o jeśli liczba ta jest ujemna.

Z zależności prądowo-napięciowych dla rezystora jest oczywiste, że

co wobec rzeczywistych, dodatnich wartości R oznacza, że napięcie na rezystorze jest w fazie z prądem tego rezystora.

Przedstawione powyżej zasady konstruowania przesunięć kątowych między wektorami prądu i napięcia umożliwiają podanie ogólnych zasad postępowania przy konstruowaniu wykresu wektorowego dla dowolnego obwodu RLC.

Dla cewki obowiązuje

co oznacza, że napięcie na cewce wyprzedza prąd o kąt
.

Podobnie napięcie na kondensatorze opóźnia się względem swojego prądu o kąt
, gdyż

Wykres wektorowy z definicji uwzględnia przede wszystkim przesunięcia kątowe między poszczególnymi wektorami. Relacje ilościowe (długości) poszczególnych wektorów są mniej istotne i zwykle uwzględniane w sposób jedynie przybliżony.

Wykres rozpoczyna się zwykle od końca obwodu (gałęzi najdalej położonej od źródła). Jeśli gałąź jest połączeniem szeregowym elementów rozpoczynamy od prądu tej gałęzi, a w przypadku połączenia równoległego - od napięcia.

Następnie rysuje się na wykresie na przemian napięcia i prądy kolejnych gałęzi, dochodząc w ten sposób do źródła. Budowę wykresu kończy się w momencie dojścia do prądu i napięcia źródłowego obwodu. Relacja wektora prądu źródłowego względem napięcia decyduje o charakterze obwodu. Jeśli napięcie wypadkowe (źródłowe) wyprzedza prąd wypadkowy lub inaczej mówiąc prąd opóźnia się względem napięcia - obwód ma charakter indukcyjny. Jeśli natomiast napięcie opóźnia się względem prądu lub prąd wyprzedza napięcie - mówimy o charakterze pojemnościowym obwodu. Jeśli nie istnieje przesunięcie fazowe prądu wypadkowego względem napięcia (kąt fazowy równy zeru) mówimy o tzw. stanie rezonansu obwodu, lub po prostu charakterze rezystancyjnym danego obwodu. Charakter rezystancyjny obwodu może powstać nawet przy istnieniu w obwodzie indukcyjności i pojemności w przypadku gdy następuje kompensacja odpowiednich składowych indukcyjnej i pojemnościowej wektorów

Obwód szeregowy RLC

Szeregowy obwód RLC składa się z szeregowo połączonych : rezystancji , indukcyjności i pojemności. Napięcie chwilowe między zaciskami zewnętrznej części takiego układu jest sumą algebraiczną napięć na poszczególnych częściach obwodu

u = u_R + u_L + u_C

Wartość skuteczna napięcia doprowadzonego do zacisków układu jest suma geometryczną napięć składowych U_L , U_R , U_C . Należy pamiętać o tym że napięcia U_L i U_C są przesunięte w fazie względem napięcia U_R odpowiednio o + 90 ⁰ i - 90 ⁰. Poniższy rysunek przedstawia wykres wskazowy dla takiego przypadku:

U² = U_R² + (U_L - U_C)²

U = √ (IR)² + (IX_L - IX_C)² = I √ R² + (X_L - X_C)²

Wyrażenie pod pierwiastkiem nazywa się opornością pozorną (impedancją) i często oznacza się literą Z

Z = √ R² + (X_L -X_C)²

Jest to pierwiastek z sumy kwadratów oporności czynnej i biernej , gdzie oporność bierna jest sumą geometryczną oporności biernej pojemnościowej i oporności biernej indukcyjnej występujących w obwodzie.

Obwody zasilane prądem zmiennym, zawierające elementy czynne i bierne powodują przesunięcia fazowe pomiędzy prądem a napięciem. Kąt przesunięcia fazowego jest określony przez arctg stosunku oporności biernej od oporności czynnej:

ϕ = arctg (X_L - X_C)/R

Wzór wyrażający zależność między natężeniem prądu a napięciem : I = U/Z wyraża w najogólniejszej postaci prawo Ohma dla odcinka lub części zewnętrznej obwodu prądu przemiennego zawierającego oporność czynną i bierną .

II. Tabele pomiarowe

L.p.	[V]	[A]	u(U_)[V]	u(I_)[A]	R[Ω]	R±u(R) [Ω]
1	1	0,06	0,15	3,75x10^-3	16,67	16,18 ± 0,08
2	2	0,12						16,67
3	3	0,185						16,22
4	4	0,24						16,67
5	5	0,35						14,29
6	6	0,365						16,44
7	7	0,432						16,20
8	8	0,49						16,33
9	9	0,542						16,61
10	10	0,605						16,53
11	11	0,655						16,79
12	12	0,715						16,78

L.p.	[V]	[A]	u(U~)[V]	u(I~)[A]	Z[Ω]	Z±u(Z) [Ω]	L±u(L) [H]
1	10	0,18	0,375	7,5x10^-3	58,82	59,18 ± 0,645	181,2 ± 2,2
2	20	0,33							58,82
3	30	0,51							57,69
4	40	0,67							58,33
5	50	0,86							58,82
6	60	1,02							56,82
7	70	1,2							57,69
8	80	1,26							58,33

L.p.	[V]	[A]	u(U~)[V]	u(I~)[A]	[Ω]	XC±u(XC) [Ω]	C±u(C) [µF]
1	10	0,10	0,75	7,5x10^-3	100,0	99,90 ± 0,0158	31,8 ± 0,005
2	20	0,20							100,0
3	30	0,31							100,0
4	40	0,41							100,0
5	49	0,50							100,0
6	60	0,61							100,0
7	70	0,71							100,0
8	100	1,02							99,9

III. Obliczenia

Rezystancja - R = U/I [Ω]

Obliczenie niepewności na podstawie klasy przyrządów pomiarowych:

Wyznaczanie niepewności typu A rezystancji cewki u(R)

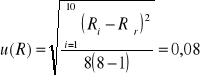
[Ω]

Impedancja Z = U/I [Ω]

Obliczenie niepewności na podstawie klasy przyrządów pomiarowych:

Z_śr = 59,2 [Ω]

Wyznaczanie niepewności typu A oporności pozornej u(Z)

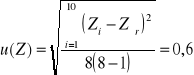
[Ω]

Obliczenie indukcyjności cewki:

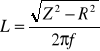
[H] = 0,181 [H] = 181 [mH]

Obliczenie niepewności u(L) metodą różniczki zupełnej:

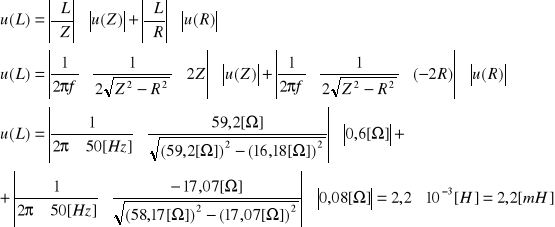
Reaktancja - X_c = U/I [Ω]

Obliczenie niepewności na podstawie klasy przyrządów pomiarowych:

X_cśr = 99,9 [Ω]

Wyznaczanie niepewności typu A oporności biernej kondensatora u(X_c):

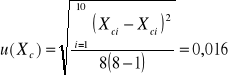
[Ω]

Obliczenie wartości pojemności kondensatora:

[F] = 3,18x10^-5 [F] = 31,8 [µF]

Obliczenie niepewności u(C) metodą różniczki zupełnej:

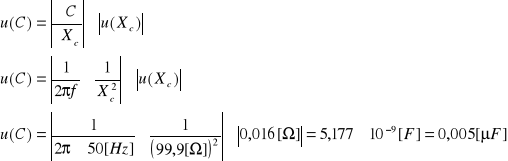
IV. Wnioski

Wartość oporu czynnego dla cewki z prądem stałym wyznaczona w ćwiczeniu wyniosła R=(16,18 ± 0,08)[Ω] .

Wartość impedancji dla cewki z prądem wyznaczona w ćwiczeniu wyniosła Z=(59,2 ± 0,6)[Ω], a jej samoindukcyjność L=(181,2 ± 2,2)[mH].

Wartość oporności biernej dla kondensatora z prądem przemiennym wyznaczona w ćwiczeniu wyniosła X_c(99,9±0,02)[Ω]. Pojemność kondensatora wyniosła C=(31,8±0,005)[μF].

13

U_C

U_L

U_R

U

U_L - U_C

---