Dane: rys

l_AB=1000m.

l_BC=200m.

δ₁=5^o

δ₂=5^o

rodzaj nosiwa: nadkład

wydajność przenośnika: Q=10000[m³/h]

szerokość taśmy: B=2,0[m.]

prędkość taśmy: v=4,0[m./s]

rodzaj taśmy: z linkami stalowymi

1. Wydajność przenośnika

1. nominalna

Q_n=F_N*v*k_A

F_N - przekrój nominalny nosiwa spoczywającego na taśmie

Dla kąta niecki λ=45^o i szerokości taśmy B= 2,0m. F_N=0,5319[m²]

k_n - współczynnik korekcyjny uwzględniający pochylenie trasy przenośnika

k_n=1-
(1-k₁)

k₁=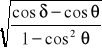

- dynamiczny kąt naturalnego usypu dla nadkładu

k₁=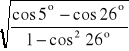
=0,98

k_n=1-
(1-0,98)=0,995

Q_n=0,53*4,0*0,995=2,12m³/s

2. masowa

Q_m.=Q_n*
ρ

ρ -dla nadkładu równe 1600kg/m³

Q_m.=2,21*1600=3392kg/s

2. Wstępny dobór taśmy

Wstępnie dobieram taśmę St 2500 o masie jednostkowej m._t=44,2kg/m²

3. Opory ruchu przenośnika

Do cięgna górnego dobieram zestaw dwukrążnikowy o parametrach:

• masa części obrotowych krążnika dolnego m._go=35,14kg

• masa całego krążnika m._g=41,9kg

• średnica krążnika D_g=0,216m

• moment bezwładności I_g=0,0329kgm²

Do cięgna dolnego dobieram zestaw dwukrążnikowy o parametrach:

• masa części obrotowych krążnika dolnego m._do=33,0kg

• masa całego krążnika m._d=39,0kg

• średnica krążnika D_d=0,194m

• moment bezwładności I_d=0,0108kgm²

Do cięgna górnego w miejscu podawania urobku dobieram zestaw nadawowy trójkrążnikowy o parametrach:

• masa części obrotowych krążnika nadawowego m._eo=66,8kg

• masa całego krążnika m._e=86,6kg

• średnica krążnika D_e=0,25m

• moment bezwładności I_e=0,0442kgm²

1. Cięgno górne

1. Odcinek AB z nosiwem

W_gAB^N=C*f*g*(m._TAB+m._kgAB+ m_NAB)*cosδ₁

C - współczynnik oporów skupionych, dla przenośników dłóższych niż 1000m.C=1,09

f - współczynnik oporów głównych , dla przenośników przesuwnych w kopalniach odkrywkowych f=0,024

g - przyspieszenie ziemskie

m_TAB - masa taśmy na odcinku AB

m_kgAB - masa części obrotowych krążników górnych na odcinku AB

m_NAB - masa nosiwa na odcinku AB

m._TAB=L_AB­*B*m_t=1000*2,0*44,2=88,400kg

m_kgAB=n_gAB*z_g*m_go+n_e*z_e*m_eo

z_g - liczba krążników w zestawie nośnym

z_e - liczba krążników w zestawie nadawowym

n_gAB - liczba zestawów krążnikóew nośnych na odcinku AB

n_e - liczba zestawów krążników nadawowych

n_gAB=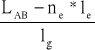

l_e - rozstaw zestawów krążników nadawowych, l_e=0,5m

l_g - rozstaw zestawów krążników nośnych, l­_g=1,2m.

n_gAB=
zestawów

m._kgAB=829*3*35,14+10*3*66,8=89397,18kg

m._NAB=
=

W_gAB^N=1,09*0,024*9,81*(88400+89397,18+848000)cos5^o

W_gAB^N=262248,17N

2. Odcinek AB od nosiwa

W_gAB=C*f*g*(m._TAB+m._kgAB)*cosδ₁

W_gAB=1,09*0,024*9,81*(88400+89397,18)cos5^o

W_gAB=45454,39N

3. Odcinek BC z nosiwem

W_gBC^N=C*f*g*(m._TBC+m._kgBC+m._NBC)*cosδ₂

m._TBC=L_BC*B*m._t=200*2,0*44,2=17680kg

m._kgBC=n_gBC*z_g*m_go

n_gBC=
=
=167 zestawów

m_kgBC=167*3*35,14=17605,14kg

m._NBC=

W_gBC^N=1,09*0,024*9,81*(17680+17605,14+169600)cos5^o

W_gBC^N=52379,51N

4. Odcinek BC bez nosiwa

W_gBC=C*f*g*(m._TBC+m._kgBC)*cosδ₂

W_gBC=1,09*0,024*9,81*(17680+17605,14)*cos5^o

W_gBC=9020,75N

2. Cięgmo dolne

1. Odcinek AB

W_dAB=C*f*g*(m_TAB+m._kdAB)*cosδ₁

m_kdAB - masa części obrotowych krążników w cięgnie dolnym

m._kdAB=n_dAB*z_d*m_do

z_d - liczba krążników w zestawie dolnym, z_d=2,0m.

n_dAB - liczba zestawów krążników dolnych na odcinku AB

n_dAB=

l­_d - rozstaw krążników w cięgnie dolnym, l_d=3,0m.

n_dAB=
=333 zestawy

m_kdAB=333*2*33=21978kg

W_dAB=1,09*0,024*9,81*(88400+21978)cos5^o

W_dAB=28218,47N

2. Odcinek BC

W_dBC=C*f*g*(m_TBC+m_kdBC)cosδ₂

M._kdBC=n_dBC*z_d*m_do

n_dBC=
zestawów

m._kdBC=67*2*33=4422kg

W_dBC=1,09*0,024*9,81*(17680+4422)*cos5^o

W_dBC=5650,44N

3. Opory całkowite ruchu

1. Wariant 1 - obie części przenośnika są obciążone

rys

W_n=W_gAB^N+W_gBC^N+W_dAB+W_dBC

W_n=262248,17+52379,51+28218,47+5650,44

W_n=348496,5

3.3.2.Wariant 2 - obie części przenośnika są nieobciążone

rys

W_n=W_gAB+W_gBC+W_dAB+W_dBC

W_n=45454,39+9020,75+28218,47+5650,44

W_n=88344,05N

3.3.3.Wariant 3 - odcinek AB obciążony, odcinek BC nieobciążony

rys

W_n=W_gAB^N+W_gBC+W_dAB+W­_dBC

W_n=262248,17+9020,75+28218,47+5650,44

W_n=305137,83N

3.3.4. Wariant 4 - odcinek AB nieobciążony, odcinek BC obciążony

rys

W_n=W_gAB+W_gBC^N+W_dAB+W_dBC

W_n=45454,39+52379,51+28218,47+5650,44

W_n=131702,81N

4. Obliczenie mocy napędu

1. Siła obwodowa niezbędna do utrzymania w ruchu taśmy

P_u=W_n*W_h

W_n - opory podnoszenia urobku

W_h=H_p*m._i*g

H_p - wysokość podnoszenia

m._i - masa jednostkowa nosiwa na taśmie

1. Wysokość i opory podnoszenia dla odcinka AB

H_pAB=L_AB*tgδ₁=1000*tg5^o=87,5m.

m._i=

W_hab.=87,5*848*9,81=727902N

2. Wysokość i opory podnoszenia dla odcinka BC

H_pBC=L_BC­­*tgδ₂=200*tg5^o= -17,5m.

W_hBC= -17,5*848*9,81= -145580,4N

Siła obwodowa dla poszczególnych wariantów obciążenia:

1 wariant - P_u=W_n+W_nAB*W_nBC=348496,59+727902-145580,4=930818,19N

2 wariant - P_u=W_n=88344,05N

3 wariant - P_u=W­_n+W­_hab.=305137,83+727902=1033039,83N

4 wariant - P_u=W_n+W_hBC=131702,81-145580,4= -13877,59N

dla wariantu 3 wystąpi największa siłą obwodowa P_u

2. Moc napędu

N_c=

- sprawność mechanizmu napędowego - przyjmuję, że w mechaniźmie napędowym zastosowano sprzęgło podatne - η_m.=0,92

N_c=

Dobieram 4 silniki SzUr 136r o mocy 1000kW każdy i 1 silnik SzUr136s o mocy 630kW

5. Sprzężenie cierne

rys

Siły obwodowe przenoszone na każdym z bębnów potraktowano jako procentowy udział mocy zainstalowanej na bębnie w stosunku do całkowitej mocy napędu przenośnika

P_I=

P_II=P_I=446237,5

P_I+P_II=P_c=892475,0N

P_k=

1. Niezbędne napięcie sił w taśmie - wstępne

S_zumin=
-dla ruchu ustalonego

S_zrmin=
- dla rozruchu

k_u, k_r - współczynniki zabezpieczenia przed poślizgiem w ruchu ustalonym i podczas rozruchu

dla płaszcza bębna wyłożonego okładziną elastyczną k_u=1,2, k_r=1,2

- współczynnik tarcia między taśmą a bębnem zależny od rodzaju okładziny bębna, nosiwa i rodzaju taśmy.

- kąt opasania taśmy na bębnie napędowym

ν_p - współczynnik nadwyżki dynamicznej występującej przy rozruchu

dla silników pierścieniowych i taśmy z linkami stalowymi ν_p=1,2

S_zumin=

S_zrmin=
I i II

przyjęto S_zmin=229400N

2. Wyznaczenie sił w taśmie

S₂=229400N

S₃=S₂+W_dBC+H_pBC*g *B*m._t=229400+5650,4+17,5*9,81*2,0*44,2=250226N

S₄=S₃+W_dAB-H_pAB*g*B*m_t=250226+28218,4-87,5*9,81*2,0*44,2=202564,0N

S₅=S₄-P_k =202564,0-140564,8=61999,2N

S₆=S₅+W_gAB^N+H_pAB*g*(m._n+B*m_t)=61999,2+262248,2+87,5*9,81*(848+2,0*44,2)=1128029,7N

S₇=S₆+W_gBC-H_pBC*g*B*m._t=1128029,7+9020,7-17,5*9,81*2,0*44,2=1121875,0N

S₂=S₁-P_c=1121875,0-892475,0=229400N

3. Sprawdzenie warunku dopuszczalnego zwisu taśmy

Na podstawie badań oporów ruchu i naprężeń w rdzeniu taśmy stwierdzono, że stosunek zwisu taśmy do rozstawu zestawów krążnikowych nie poewinien przekraczać wartości 0,015. Powyżej tej granicy zarówno naprężenia jak i opory ruchu zaczynają przyrastać coraz szybciej. Zaleca się więc, żeby siła w taśmie nie obniżyła się poniżej S_dop

S_dop=k_x*l_k­*(B*m_t+m._n)

k_x - współczynnik zależny od długości przenośnika i stanu pracy

dla L>1000m otrzymamy:

• w ruchu ustalonym k_x=120

• przy hamowaniu k_x=40

l_k - rozstaw zestawów krążnikowych

1. Cięgno górne

• ruch ustalony S_dop=120*1,2(2,0*44,2+848)=134841,6N

• przy hamowaniu S_dop=40*1,2(2,*44,2+848)=44947,2N

2. Cięgno dolne

• ruch ustalony S_dop=120*3*2,0*44,2=31824,0N

• przy hamowaniu S_dop=40*3,2,0*44,2=10608,0N

przyjmuję S_dop=134841,6N

Ponieważ S₅<S_dop należy zwiększyć siłę napinającą o ΔS=S_dop-S₅=134842-61999,2=72850N

Po korekcji sił w taśmie otrzymamy:

S₂=229400+72850=302250N

S₃=323076N

S₄=275414N

S₅=134850N

S₆=1200879,7N

S₇=1194725N

S₂=S₁-P_c=1194725-892475=302250N

6. Dobór taśmy

Sprawdzenie wytrzymałości taśmy

K_N

S_max,v - maksymalna siła w taśmie podczas rozruchu

Dla taśm z linkami stalowymi S_max,v=1,3*S_max,u

S_max,u - maksymalna siła w ruchu ustalonym S­_max,u­=S₆

S_max,v=1,3*1200879,7=1561143,6N

k_e - współczynnik bezpieczeństwa k_e=5,5 dla taśmy St 2500

=4293144,9N/m.=4293,15kN/m.>K_N

Dobrana wstępnie taśma ma za małą wytrzymałość. Należy zastosować taśmę St 4500.

7. Wyznaczenie czasu wybiegu przenośnika

t_z=V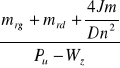

m_rg - masa zredukowana cięgna górnego [kg]

m._rg=m._T+m._n+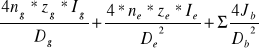

m._rd - m._T+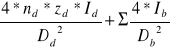

I_g, I_e, I_e, I_b - momenty bezwładności części obrotowych odpowiednio: krążnika nośnego, nadawowego, dolnego, bębna.

D_g, D_e, D_d, D_b - średnice płaszcza odpowiednio: krążnika górnego, nadawowego, dolnego, bębna.

W skład masy cięgna górnego wlicza się wszystkie bębny nie napędowe znajdujące się między bębnem napędowym czołowym, a zwrotnym. Wszystkie pozostałe bębny są wliczane w skład masy cięgna dolnego.

I_m.­ - moment bezwładności mechanizmu napędowego zredukowany na wał bębna napędowego.

I_m.=n(I_w+I_s+I_p)*i²*η_m.+I_n [kg/m²]

n - ilaść zastosowanych zestawów napędowych

I_w, I_s­, I_p­, I_n­ - momenty bezwładności odpowiednio: wirnika silnika, sprzęgła, przekładni, bębna napędowego

i - przełożenie przekładni

Zastosowano następujące bębny:

1. 2 bębny napędowe dwustronne o średnicy 2,0m i I_b=315kg/m²

2. 1 bęben napędowy jednostronny o średnicy 1,25m. i I_b=50,9kg/m²

3. 1 bęben napinający o średnicy 0,63m. i I_b=5,14kg/m²

4. 2 bębny odchylające o średnicy 0,365m. i I_b=1,06kg/m²

m._rg=106080+1017600+

m._rg=1132318,0kgm²

m._rd=106080+

m_rd=107000,0kgm²

Dobór przełożenia przekładni

Dla średnicy bębna napędowego wynoszącej 2,0m., prędkości obrotowej silnika równej 1000obr/min i prędkości taśmy v=4,0m/s przełożenie przekładni wyniesie: i=25.

Zastosuję przekładnię A1-630-25 o parametrach:

i= 25

N=630kW

I_p=0,69kgm²

Do tego zastosowano sprzęgło elastyczne o średnicy tarczy hamulca 0,8m. I_s=2,6kgm²

Silnik SZUr 136r, I_w=14,05kgm²; η_m.=0,93

Silnik SZUr 136s, I_w=12,20kgm²; η_m.=0,91

Dla średnicy bębna napędowego 1,25m., prędkości silnika 1000obr/min, prędkości taśmy v=4,0m/s przełożenie przekładni wyniesie i=16

Zastosuję przekładnię: A1-630-10

i=18

N=630kW

I_p=0,76kgm²

Do tej przekładni zastosowano sprzęgło elastyczne o średnicy tarczy hamulca 0,5m, i_s=0,23kgm²

I_m=[4*(14,05+2,6+0,69)*25²*0,93+2*3,15]+[1(12,2+0,76+0,23)*16²*0,91*54

I_m=44069,2kgm²

t_z=4,0*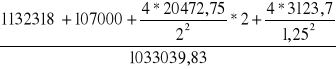

t_z=4,99[s]

Złożono czas hamowania t_h=8s, t_z<t_h - nie ma konieczności stosowania hamulca

Ponieważ przedmiotem projektu jest długi przenośnik nachylony należy sprawdzić, czy urobek znajdujący się na taśmie nie wprawi jej w ruch. Ze względu na bezpieczeństwo zakłada się przy tym, że opory ruchu są dwukrotnie mniejsze od obliczonych przy doborze napędu. W projekcie największe niebezpieczeństwo ruchu taśmy pod wpływem ciężaru urobku zachodzi gdy nosiwo zapełnia odcinek A- B - wariant III.

Jeżeli dla wyszczególnionych warunków jest spełniona poniższa nierówność to należy zastosować hamulec zapadujący po zatrzymaniu przenośnika

W_h'>0,5W_h'

W_hAB>0,5(W_hAB^N+W_hBC)=0,5(W_gAB^N+W_dAB+W_gBC+W_dBC)

727902>0,5*305137,83

727902N152569N

Zostanie zastosowany hamulec zapadający po zatrzymaniu przenośnika.

Wymagany moment hamulca przy dwukrotnym wsp. bezpieczeństwa

M_h=(W_h'+0,5W_h')

M_h=(-727902+0,5*305137,83)

8. Wyznaczenie odcinków przejściowych

1. Minimalna dopuszczalna odległość zestawu krążnikowego od bębna zrzutowego

L_c=C_c*B

C_c=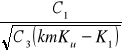

C₁ - współczynnik kształtu - dla kąta niecki
i C₁=150

C₃ - współczynnik uwzględniający własności taśmy - dla taśm St C₃=26,4

K_u - dopuszczalne naprężenie użyteczne taśmy

K_u=0,1*K_n=0,1*4500=450kN/m

K₁ - naprężenie w taśmie nabiegojącej na bęben zrzutowy

K₁=

k_m - współczynnik określający maksymalne lokalne dopuszczalne naprężenie. Dla taśm z linkami stalowymi k_m=2,0

C_c=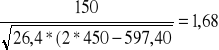

L_c=1,68*2,0=3,36m

2. sprawdzenie stateczności poprzecznej taśmy

k_p^'=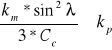

dla taśm z linkami stalowymi k_p=0,09

k_p^'=

Powyższy warunek nie jest spełniony, odległość zestawu oblicza się więc ze wzoru

L_c=C_c'*B

Gdzie współczynnik C_c^' wyznacza się z nierówności

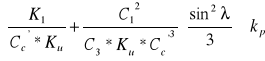
C_c^'=2,9

L_c=2,9*2,0=5,8m

4. Minimalna dopuszczalna odległość zestawu krążnikowego od bębna zwrotnego

L_z=C_z*B

C_z=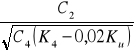

K₄ - naprężenie w taśmie zbiegającej z bębna zwrotnego

K₄=

C₂ - współczynnik kształtu dla λ=45^o C₂=82

C₄ - współczynnik uwzględniający jakość taśmy. Dla taśmy St C₄=70

C_z=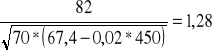

L_z=1,28*2,0=2,56m

5. Sprawdzenie stateczności poprzecznej taśmy

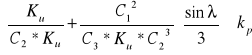
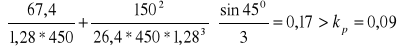
Ponieważ powyższy warunek nie został spełniony z nierówności wyznaczamy wartość C_z^' wstawiając ją zamiast C_z

C_z^'=1,62

L_z=C_z^'*B=1,62*2,0=3,24m

9. Wyznaczenie łuku przejściowego

Poprawne układanie się taśmy na łuku uzyska się gdy promień łuku wewnętrznego nie będzie mniejszy od wartości obliczonych ze wzoru

R_w=

S_i - siła w taśmie na łuku.

Wartość tej siły oblicza się dla najniekorzystniejszych warunków obciążenia przy założeniu, że taśma nie jest obciążona tylko na łuku.

W projekcie najniekorzystniejszy wariant obciążenia ma miejsce dla rozkładu nosiwa jak na schemacie III i I. S_i=S₆. Jeżeli kąt nachylenia przenośnika δ nie przekracza 18^o to krzywą łańcuchową można zastąpić łukiem koła. W projekcie wykorzystano takie rozwiązanie.

R_w=

Rys

OA=OB^'=R_w*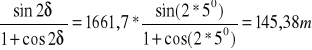

OB=OB^'=145,38m

y=

BB^'=y_max=R_w*

10. Trajektoria spadającego urobku

Urobek leżący na taśmie oddziela się na bębnie zrzutowym pod wpływem działania siły odśrodkowej F_odśr. Oderwanie się urobku od taśmy następuje wówczas gdy siła odśrodkowa F_odśr zrównoważy składową siły ciężkości G skierowaną promieniowo w kierunku osi bębna.

F_odśr=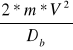
G=m*g

Rys

10.1 . Warunek oderwania się urobku od taśmy

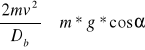
O miejscu oderwania się urobku od taśmy decyduje prędkość taśmy v. W szczególnym przypadku warunek ten może nastąpić w punkcie nabiegania na bęben, jeżeli v=v_gr

V_gr=

V_gr=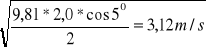

Ponieważ v=4,0m/s>v_gr urobek oderwie się od taśmy w miejscu nabiegania taśmy na bęben.

Ponieważ taśma nabiega na bęben za prostą symetrii bębna więc nie ma możliwości ponownego spadnięcia urobku na taśmę.

10.2. Dolna krzywa zrzutu

y=

y=

X	[m]	0,5	1,0	1,5	2,0	2,5	3,0	3,5
Y	[m]	0,077	0,307	0,690	1,226	1,916	2,759	3,755

10.3. Górna krzywa zrzutu

y^'=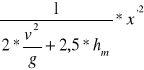

przyjęto h_m=0,4m

y^'=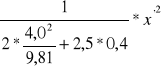
=0,2346*x^'2

X^'	[m]	0,5	1,0	1,5	2,0	2,5	3,0	3,5
Y^'	[m]	0,059	0,235	0,528	0,938	1,466	2,112	2,874

14

---