1. Wstęp Teoretyczny

Niezależny pomiar koncentracji nośników ładunku i charakteryzującej ich ruchliwości jest możliwy dzięki zjawisku Halla. Pomiar napięcia Halla umożliwia wyznaczenie koncentracji i, dodatkowo, także znaku nośników ładunku w danym materiale. Zatem kombinacja napięcia Halla i przewodnictwa właściwego, umożliwia wyznaczenie obu parametrów łącznie charakteryzujących własności elektryczne danego materiału.

Efekt Halla jest zjawiskiem fizycznym polegającym na tym, że w przewodniku z prądem o natężeniu I umieszczonym w polu magnetycznym o indukcji B powstaje poprzeczne do prądu i prostopadłe do pola magnetycznego napięcie elektryczne E_H tzw. napięcie Halla U_H.

Stała Halla zwana także współczynnikiem Halla [dla elektronów; półprzewodników typu n o ładunku nośnika -e]wyrażana jest wzorem:

R_H = -

Dla ładunków dodatnich stała Halla określona jest przez koncentrację dziur p czyli liczbę ładunku dodatniego w jednostce objętości. Wyraża się ona wzorem:

R_H =
.

natomiast napięcie Halla charakteryzuje poniższy wzór:

U_H = R_H

Przy czym :

I - oznacza natężenie prądu płynącego przez próbkę,

S - pole przekroju próbki, przez które przepływa prąd,

n - koncentracja elektronów ( liczbą elektronów w jednostce objętości )

Napięcie Halla jest wprost proporcjonalne zarówno do natężenia I prądu przepływającego przez próbkę, jak i do wielkości wektora indukcji magnetycznej B pola magnetycznego, w którym umieszczono próbkę.

Gdy nośnikami prądu są elektrony, przez próbkę płynie prąd i wytworzone zostaje pole elektryczne E o kierunku zgodnym z kierunkiem płynącego prądu. Elektrony poruszają się natomiast w kierunku przeciwnym polu z prędkością V_x.

Gdy płytkę umieścimy w polu magnetycznym, na poruszające się elektrony dodatkowo działać będzie siła Lorentza F_L, pod której wpływem każdy z płynących elektronów zostanie odchylony od pierwotnego kierunku.

Wskutek zmiany toru ruchu elektrony gromadzić się będą na jednej krawędzi płytki, równocześnie zaś powstanie ich niedobór na drugiej krawędzi. Dzięki temu wytworzone zostaje dodatkowe pole elektryczne E_H. Zjawisko to trwa do momentu, w którym działająca na elektrony siła pochodząca od tego pola zrównoważy F_L.

2. Przebieg pomiarów

Celem niniejszego ćwiczenia jest:

• ustalenie prawidłowości rządzących efektem Halla oraz wyznaczenie stałej Halla,

• wyznaczenie koncentracji i ruchliwości nośników prądu w germanie ( typu p lub n ),

• wyciągnięcie wniosków dotyczących rodzaju przewodnictwa w badanej próbce.

Cel ten osiągnę analizując:

1. zależność napięcia Halla U_H od natężenia prądu I przepływającego przez próbkę, gdy jest ona umieszczona w stałym polu magnetycznym o indukcji B,

2. zależność napięcia Halla U_H od wielkości indukcji B pola magnetycznego, gdy przez próbkę przepływa prąd o stałym natężeniu I.

Maksymalne wartości i parametry badanej próbki:

• natężenia prądu: I_max = 40 mA

• natężenia pola magnetycznego: B_max = 250 mT.

• Opór w temperaturze pokojowej: R₀ = 60 Ω

• Pole przekroju: S = (1,0 ± 0,1) · 10^-5 m²

• Grubość próbki: d = (1,0 ± 0,1) · 10^-3 m

• Długość próbki: l = (0,020 ± 0,01) m

3. Pomiary

U_H = f(I)

B[T]	100
I[mA]	-40	-35	-30	-25	-20	-15	-10	-5
UH[mV]	-34,4	-30,5	-25,2	-21	-16	-11	-6,4	-2,5

B[T]	100
I[mA]	0	5	10	15	20	25	30	35	40
UH[mV]	2,2	8,1	12,4	17,6	21,3	24,6	29	33,2	36,6

B[T]	200
I[mA]	-40	-35	-30	-25	-20	-15	-10	-5
UH[mV]	-72	-61,5	-54	-43,7	-33,6	-25,3	-16,1	-7,1

B[T]	200
I[mA]	0	5	10	15	20	25	30	35	40
UH[mV]	2,2	13	21,9	29,9	38,2	47,4	57,4	63	70,4

U_H=f(B)

I[mA]	10
B[T]	25	50	75	100	125	150	175	200	225	250
UH[mV]	4,3	6,6	9,0	11,5	13,7	16	18,1	20,3	22,2	24,3

I[mA]	20
B[T]	25	50	75	100	125	150	175	200	225	250
UH[mV]	6,3	11,3	16,3	21,4	26,0	30,8	35,4	39,9	44,3	48,8

4. Opracowanie wyników

1. Pomiar U_H= f(I)

• Wykres dla B = 200 mT

• Wykres dla B = 100 [mT]

• Analizując powyższe wykresy dla ustalonych wartości B stwierdzam, że U_H zależy liniowo od I, co jest zgodne z założeniami wynikającymi z równań:

U_H =
oraz U_H = R_H

• Wyznaczamy współczynniki kierunkowe prostych regresji będących wykresami zależności U_H = f ( I ).

Wykorzystując metodę najmniejszych kwadratów, w której współczynnik kierunkowy a prostej jest współczynnikiem nachylenia dla wzoru y= a x + b. Podaję także błąd wyznaczania podanych współczynników. Do obliczeń wykorzystuję program OPRA Wer. 8:

Dla B = 200[mT] : a = 1,81 Δa = 0,01 b= 1,77 Δb= 0,37

Dla B = 100[mT] : a = 0,91 Δa = 0,01 b = 2,23 Δb= 0,23

• Korzystając z równania
  przekształcam je do postaci
  
  

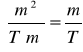
Za jego pomocą określam znak i szacuję stałą Halla, przy ustalanej indukcji B.

Dla B = 200[mT] :
= 0,0905

Dla B = 100[mT] :
= 0,091

Dla dodatnich wartości indukcji pola magnetycznego, stała Halla zmniejsza się wraz ze wzrostem wartości B. Stała Halla jest dodatnia to oznacza, że mamy do czynienia z ładunkami dodatnimi. Dla takich ładunków stała Halla jest określona poprzez koncentrację dziur.

• Poprzez analizę wzoru
  , korzystając z metody różniczki zupełnej, docieramy do wzoru, który pozwala nam na obliczenie ΔR_H

Dla B = 200[mT] :
= 0,0005
R_H = (0,0905 ± 0,0005)

Dla B = 100[mT] :
= 0,001
R_H = (0,091 ± 0,001)

2. Pomiar U_H= f(B)

Wykres dla I = 10[mA]

Wykres dla I = 20[mA]

• Analizując powyższe wykresy dla ustalonych wartości I stwierdzam, że U_H zależy liniowo od B, co jest zgodne z założeniami wynikającymi z równań:

U_H =
oraz U_H = R_H
.

• Wyznaczam współczynniki kierunkowe prostych regresji będących wykresami zależności U_H = f ( I ) .

Wykorzystując metodę najmniejszych kwadratów, w której współczynnik kierunkowy a prostej jest współczynnikiem nachylenia dla wzoru y= a x + b. Podaję także błąd wyznaczania podanych współczynników. Do obliczeń wykorzystuję program OPRA Wer. 8

Dla I = 10[mA] : a = 0,09 Δa = 0,001 b= 2,34 Δb= 0,17

Dla I = 20[mA] : a = 0,18 Δa = 0,001 b = 2,10 Δb= 0,25

• Korzystając z równania
  i przekształcając je do postaci
  
  

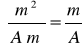
określam znak i szacuję stałą Halla, przy ustalanym prądzie I sterującym próbką:

Dla I = 20[mA] :
= 0,090

Dla I = 10[mA] :
= 0,095

Dla dodatnich wartości natężenia prądu, stała Halla zwiększa się wraz ze wzrostem wartości I.

• Poprzez analizę wzoru
  , korzystając z metody różniczki zupełnej, docieramy do wzoru, który pozwala nam na obliczenie ΔR_H

Dla I = 20[mA] :
= 0,0005
R_H =( 0,0900 ± 0,0005)

Dla I = 10[mA] :
= 0,001
R_H = (0,095 ± 0,001)

3. Obliczanie koncentracji i ruchliwości nośników prądu

Obliczam koncentrację nośników ładunków, którymi są ładunki dodatnie, korzystając ze wzoru:
. Następnie obliczam ruchliwość prądu µ ze wzoru:
gdzie
jest przewodnictwem próbki, zaś l długością próbki.

• Dla B = 100 mT n = 6,83 · 10¹⁹
  µ = 3,91· 10^-36
  

• Dla B = 200 mT n = 6,86 · 10¹⁹
  µ = 3,90· 10^-36
  

• Dla I = 10 mA n = 6,54 · 10¹⁹
  µ = 4,00· 10^-36
  

• Dla I= 20 mA n = 6,90 · 10¹⁹
  µ = 3,89· 10^-36
  

• Błąd wyznaczenia koncentracji, wyznaczony za pomocą metody różniczki zupełnej.

Czyli ostatecznie:

• Dla B = 100 mT n = 7,5 · 10¹⁷
  

• Dla B = 200 mT n = 3,7 · 10¹⁷
  

• Dla I = 10 mA n = 3,44 · 10¹⁷
  

• Dla I= 20 mA n = 7,67 · 10¹⁷
  

5. Wnioski

Na podstawie analizy zależności napięcia Halla U_H od natężenia prądu I przepływającego przez próbkę, gdy jest ona umieszczona w stałym polu magnetycznym o indukcji B, oraz zależności napięcia Halla U_H od wielkości indukcji B pola magnetycznego, gdy przez próbkę przepływa prąd o stałym natężeniu I stwierdzam, że w badanym materiale nośnikami ładunku są ładunki dodatnie. Użyta próbka germanu to półprzewodnik typu p.

Zastosowane przeze mnie wzory użyte do obliczeń stałej Halla nie dają dokładnych wyników wartości obliczanych, ponieważ w przypadku opisu transportu nośników prądu w półprzewodniku należy jeszcze uwzględnić statystyczny rozkład prędkości nośników, a więc wziąć pod uwagę mechanizmy ich rozpraszania. Różnice w zachowaniu się układu są powodowane także różną ilością elektronów swobodnych w materiałach. Dodatkowo na dokładność pomiarów wpływa również dokładność użytych w obliczeniach wielkości, ponieważ każda nich obarczona jest pewnym błędem.

n= (6,83 ±0,075)·10¹⁹

n= (6,86 ±0,037)·10¹⁹

n= (6,54 ±0,034)·10¹⁹

n= (6,90 ±0,077)·10¹⁹

---