MECHANIKA PŁYNÓW

ZADANIA VI

Równanie Bernulliego

1. Wiadomości teoretyczne

Równanie Bernuliego, wzór Torricellego, płaskie przepływy płynów doskonałych.

2. Zadania

1. Swobodna powierzchnia wody w zbiorniku otwartym o bardzo dużej średnicy jest położona na wysokości z₁ = 50 m. Obliczyć prędkość v₂ wody na wylocie dyszy, strumień objętości wody
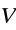
   oraz prędkość v wody w rurociągu, jeżeli średnice rurociągu oraz dyszy wynoszą odpowiednio
   d = 100 mm i d₂ = 40 mm. Wylot dyszy znajduje się na wysokości z₂ = 5 m.

2. Z dużego i otwartego zbiornika prostokątnego o przekroju a x b = 2 x 1.2 m przez przewód wypływa woda do atmosfery. Wysokość wody w zbiorniku h₀ = 1.2 m. Średnice przewodu: d₁ = 100 mm, d₂ = 70 mm, d₃ = 50 mm. Określić objętościowe natężenie przepływu wypływającej wody i prędkości w przewodach. Wysokości h₁ = 0.5 m i h₂ = 2.4 m.

3. Powietrze o temperaturze 20 ^oC płynie rurociągiem. Pierwszy manometr wodny wskazuje różnice poziomów h_s = 16 mm, drugi h_c = 24 mm. Obliczyć prędkość powietrza, traktując go jako gaz nieściśliwy.

4. Do pomiaru prędkości przepływu powietrza użyto sondy Prandla wraz z manometrem spirytusowym. Obliczyć prędkość powietrza, jeżeli spiętrzenie manometru z = 60 mm, temperatura powietrza T = 473 K, ciśnienie powietrza p = 0.15 MPa, gęstość spirytusu ρ_s = 800 kg/m³.

5. Zwężka Venturiego, służąca jako przepływomierz ma średnice: D₁ = 0,24 m, D₂ = 0,08 m. Manometr rtęciowy wskazuje różnicę poziomów h_m = 0,4 m. Obliczyć natężenie przepływu wody.

6. Ze zbiornika wypływa woda przez kanał składający się z dwóch odcinków o średnicy D = 30 mm
   i d = 20 mm Obliczyć prędkość wody w obu odcinkach oraz ciśnienie w odcinku kanału o większej średnicy. Dane do zadania: h = 4 m, p_a = 991 hPa, średnica zbiornika dużo większa od średnic obu odcinków.

7. Tunel aerodynamiczny o średnicy d₁ = 1200 mm ma otwartą część pomiarową, w której średnica strugi wynosi d₂ = 500 mm. Znaleźć prędkość powietrza v₂, jeżeli wskazanie manometru wodnego z = 200 mm. (gęstość powietrza 1,29 kg/m³)

8. Wentylator zasysa powietrze z atmosfery, gdzie panuje ciśnienie p_o = 100 kPa i temperaturę 20 ^oC. Przewód ma średnicę D₂ = 0,3 m, obudowa piasty D₁ = 0,15 m. Podciśnienie na wlocie jest równoważne ciśnieniu hydrostatycznemu słupa wody o wysokości h = 280 mm. Obliczyć strumień masy powietrza w przewodzie.

9. W dużym otwartym zbiorniku znajduje się ciecz doskonała sięgająca wolnym zwierciadłem nad otworem wypływowym na wysokość H = const. Wyznaczyć średnią prędkość c₂ w przekroju 2 oraz wysokość z₃ , na jaką podniesie się strumień cieczy wypływający ze zbiornika.

10. W zbiorniku, w którym jest utrzymywany stały poziom wody, panuje nadciśnienie p = 50 kPa. Obliczyć, na jaką wysokość H₂ wzniesie się strumień wody, jeżeli odległość między poziomem cieczy w zbiorniku a wylotem H₁ = 2 m.

11. Dwa sąsiadujące ze sobą zbiorniki mają w ścianach bocznych otwory o średnicach d₁ i d₂. Wiedząc, że różnica poziomów wody w zbiornikach jest stała i wynosi H = 1 m, a głębokość zanurzenia otworu o średnicy d₂ jest równa H₁ = 2.5 m, obliczyć prędkość wypływu cieczy c₂ i c₃ oraz stosunek średnic d₁/d₂. Straty w otworach pominąć.

12. Przy zamkniętym zaworze nadciśnienie w przewodzie wynosi p = 2060 mmHg, przy otwartym zaś spada do p₁ = 440 mmHg. Określić objętościowe natężenie przepływu przez przewód, jeśli średnica przewodu d = 20 mm

---