Nr ćwicz. 201 |
Data: 05.05.2012r |
Imię i Nazwisko Paweł Nawrocki |
Wydział Elektryczny |
Semestr I |
Grupa E7 nr lab. 1 |
prowadzący
|
Przygotowanie: |
Wykonanie: |
Ocena ostat. : |
||
Temat : Wyznaczanie zależności przewodnictwa od temperatury dla półprzewodników i przewodników .
Wstęp teoretyczny
Prawo Ohma stwierdza , że :
![]()
,
gdzie j - gęstość prądu ,
E - natężenie pola elektrycznego ,
- przewodnictwo elektryczne .
Przewodnictwo elektryczne określone jest wzorem :
![]()
n , p - koncentracje nośników ,
n , p - ruchliwość nośników .
Ponieważ koncentracja i ruchliwość zależą od temperatury i rodzaju materiału , więc przewodnictwo elektryczne także zależy od tych czynników .
O zależności temperaturowej przewodnictwa w metalach decyduje tylko zmniejszanie się ruchliwości wraz ze wzrostem temperatury ( koncentracja nośników - elektronów - jest bardzo duża i nie zależy od temperatury ) . Zależność temperaturową wyraża się poprzez opór (R1/ ) :
![]()
,
R0 - opór w temperaturze T0 ,
- średni współczynnik temperaturowy .
W półprzewodnikach decydujący wpływ na przewodnictwo ma koncentracja nośników. W przypadku półprzewodników samoistnych koncentracja elektronów i dziur jest taka sama i wynosi :
![]()
,
Eg - szerokość pasma zabronionego .
Natomiast w półprzewodnikach domieszkowych koncentracje określone są poprzez poziomy energetyczne (zależnie od typu półprzewodnika ) Ed - donorowy , Ea - akceptorowy , oraz poprzez temperaturę :
![]()
.
Uwzględniając powyższe równania otrzymujemy wzór na temperaturową zależność przewodnictwa dla półprzewodników :
![]()
,
Edom jest jedną z wielkości Ed lub Ea zależnie od typu półprzewodnika .
W odpowiednio niskich temperaturach można zaniedbać w powyższym wzorze pierwszy składnik , natomiast w wysokich temperaturach ( po nasyceniu poziomów domieszkowych ) można zaniedbać składnik drugi . Odpowiednio dla tych dwóch przypadków wzór przyjmie postać :
![]()
.
Logarytmując jeden z powyższych wzorów otrzymamy zależność :
` ![]()
Z wykresu tej zależności wygodnie jest odczytać zależność przewodnictwa od temperatury :
Zasada pomiaru
Pomiarów oporu półprzewodnika i przewodnika dokonuje się w różnych temperaturach . Badane materiały umieszczone są w ultratermostacie , a ich opory mierzy się przy pomocy mostka Wheatstone'a .
Pomiary
Tabela wartości pomiarów dla przewodnika wraz z obliczonym oporem Rx
T |
R |
R1 |
R2 |
Rx |
[oC] |
[] |
[] |
[] |
[] |
25 |
1121 |
1 |
10 |
112,1 |
30 |
1143 |
1 |
10 |
114,3 |
35 |
1162 |
1 |
10 |
116,2 |
40 |
1192 |
1 |
10 |
119,2 |
45 |
1197 |
1 |
10 |
119,7 |
50 |
1216 |
1 |
10 |
121,6 |
55 |
1230 |
1 |
10 |
123 |
60 |
1247 |
1 |
10 |
124,7 |
65 |
1270 |
1 |
10 |
127 |
70 |
1285 |
1 |
10 |
128,5 |
Przykładowe obliczenia:
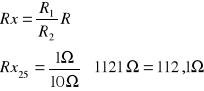
T |
R |
R1 |
R2 |
Rx |
[oC] |
[] |
[] |
[] |
[] |
25 |
2430 |
100 |
1 |
243000 |
30 |
1895 |
100 |
1 |
189500 |
35 |
1596 |
100 |
1 |
159600 |
40 |
1294 |
100 |
1 |
129400 |
45 |
1080 |
100 |
1 |
108000 |
50 |
874 |
100 |
1 |
87400 |
55 |
739 |
100 |
1 |
73900 |
60 |
621 |
100 |
1 |
62100 |
65 |
516 |
100 |
1 |
51600 |
70 |
439 |
100 |
1 |
43900 |
![]()
Analiza pomiarów
Błąd pomiaru rezystancji mostkiem Wheatstone'a : R=0.1
Błąd pomiaru temperatury : T=0.5C
Zamiana wartości temperatur ze stopni Celsjusza na Kelwiny
C |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
65 |
70 |
K |
298,15 |
303,15 |
308,15 |
313,15 |
318,15 |
323,15 |
328,15 |
333,15 |
338,15 |
343,15 |
Wykres zależności R=f(T) dla przewodnika
Wykres zależności R=f(T) dla półprzewodnika
Tabela zależności T, R, z obliczonymi ln(1/R) oraz 1/T dla półprzewodnika:
T [K] |
R [Ω] |
ln(1/R) |
1/T |
298,15 |
243000 |
-5,6976 |
0,003354 |
303,15 |
189500 |
-5,71423 |
0,003299 |
308,15 |
159600 |
-5,73059 |
0,003245 |
313,15 |
129400 |
-5,74668 |
0,003193 |
318,15 |
108000 |
-5,76252 |
0,003143 |
323,15 |
87400 |
-5,77812 |
0,003095 |
328,15 |
73900 |
-5,79347 |
0,003047 |
333,15 |
62100 |
-5,80859 |
0,003002 |
338,15 |
51600 |
-5,82349 |
0,002957 |
343,15 |
43900 |
-5,83817 |
0,002914 |
Przykładowe obliczenia:
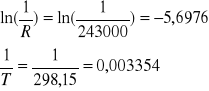
Wykres zależności ln(1/R) do 1/T:
Współczynnik nachylenia prostej ln(1/R)=f(1/T) obliczony metodą regresji wynosi :
a= -3863,61
a= 27.95.
Poziom domieszkowy będzie zatem równy :
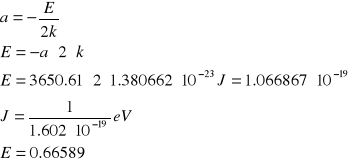
![]()
Błąd wyznaczenia poziomu domieszkowego :
![]()
Wynik:
E=(0.6660.0015)eV
Wyszukiwarka
Podobne podstrony:
sprawko 202, Szkoła, Politechnika 1- 5 sem, politechnika, rok 1, 2 semestr, wszystko 2 sem
sprawka, Szkoła, Politechnika 1- 5 sem, politechnika, rok 1, 2 semestr, wszystko 2 sem
Brudnopis, Szkoła, Politechnika 1- 5 sem, politechnika, rok 1, 2 semestr, wszystko 2 sem
L.Dł.Bez.Strat - zadanie 3, Szkoła, Politechnika 1- 5 sem, politechnika, rok 2, teoria pola
Cw 10, Szkoła, Politechnika 1- 5 sem, politechnika, rok 1, 2 semestr, wszystko 2 sem
wzmacniacz operacyjny - zastosowanie nieliniowe, Szkoła, Politechnika 1- 5 sem, chomikuj, 4 sem (gra
z1-wniosek-o-sp 0, Szkoła, Politechnika 1- 5 sem, politechnika, rok 1, 2 semestr, wszystko 2 sem
zaliczenie TM - E4 2, Szkoła, Politechnika 1- 5 sem, politechnika, 3 rok, technika mikroprocesorowa
POLITECHNIKA POZNAŃSKA, Szkoła, Politechnika 1- 5 sem, politechnika, rok 1
z4-podanie-sp 0, Szkoła, Politechnika 1- 5 sem, politechnika, rok 1, 2 semestr, wszystko 2 sem
POLITECHNIKA POZNAŃSKA1, Szkoła, Politechnika 1- 5 sem, politechnika, rok 1
ogniwo paliwowe1, Szkoła, Politechnika 1- 5 sem, politechnika, rok 2, sem 4
MAro sprawo z fiz, Szkoła, Politechnika 1- 5 sem, politechnika, rok 1
Eleny Paszylk wszystko, Szkoła, Politechnika 1- 5 sem, SEM IV, Elektroenergetyka. Laboratorium, Prze
ćw. 4 Elementy RLC w obwodzie prÄ…du sinusoidalnie zmiennego, Szkoła, Politechnika 1- 5 sem,
Sprawozdanie - renegat nasza wersja ad.2009 v3 (1), Szkoła, Politechnika 1- 5 sem, politechnika, 3 r
brudnopis cw 5121, Szkoła, Politechnika 1- 5 sem, politechnika, rok 1
brudnopis, Szkoła, Politechnika 1- 5 sem, politechnika, rok 1, politechnika
więcej podobnych podstron