AKADEMIA TECHNICZNO - HUMANISTYCZNA

W BIELSKU - BIAŁEJ

INSTYTUT OCHRONY ŚRODOWISKA I INŻYNIERII ŚRODOWISKA

ĆWICZENIE 3

OBLICZANIE PRZEPŁYWÓW MAKSYMALNYCH ROCZNYCH W PRZEKROJU WODOWSKAZOWYM O OKREŚLONYM PRAWDOPODOBIEŃSTWIE PRZEWYŻSZENIA

Marzena Bartniczak

Rok studiów 2

Grupa 1

Bielsko - Biała , 2004

Spis treści

Strona

1. Określenie równania krzywej objętości przepływu (konsumpcyjnej) 3

1. Wyznaczenie stałej „B” 3

1. Określenie stałej „B” metodą Głuszkowa 4

2. Wyznaczenie parametrów „a” i „n” 6

2. Obliczanie przepływów maksymalnych rocznych 9

3. Opracowanie ciągu rozdzielczego przepływów maksymalnych 10

4. Estymacja parametrów rozkładu Persona typ III 11

5. Obliczanie przepływów maksymalnych rocznych o określonym prawdopodobieństwie pojawiania się 12

6. Obliczanie wartości przedziału ufności 13

1. Określenie równania krzywej objętości przepływu (konsumpcyjnej)

Kształt równania krzywej objętości przepływu oddaje krzywa potęgowa n-tego stopnia.

Równanie tej krzywej nosi nazwę równania Harlachera i przyjmuje postać:

(1)

gdzie:

Q - przepływ

H - stan wody cm

a , n - parametry równania

Stan wody H powiązany jest z napełnieniem T zależnością:

T=H+B (2)

Jednakże aby określić stan napełnienia oraz krzywą objętości przepływu musimy wyznaczyć wartość stałej „B” oraz parametry „a” i „n”.

1. Wyznaczenie stałej „B”

Odcięte punktu dennego krzywej przepływu czyli odczyt na wodowskazie przy którym Q=0 można określić kilkoma metodami opierając się na pomiarach lub konstrukcjach graficznych.

Do najczęstszych stosowanych metod należą:

• metoda poprzecznego przekroju cieku

• metoda z profilu podłużnego dna

• metoda Głuszkowa

• metoda prób z wykresu krzywej przepływu w podziałce logarytmicznej

W moim przypadku będę stosowała metodę Głuszkowa.

1. Określenie stałej „B” metodą Głuszkowa

Metoda ta opiera się na odręcznie wyrównanej krzywej przepływu. Na tej krzywej obiera się dwa oddalone od siebie punkty których współrzędne wynoszą odpowiednio Q₁ H₁ i Q₂ H₂ . Staramy się je tak wybrać aby stan H₁ był w przybliżeniu równy najniższemu stanowi a H₂ nie przekroczył punktu zdecydowanej zmiany krzywizny wykresu tzn. punktu przełomu lub punktu brzegowego krzywej przepływu.

Następnie oblicza się średnią geometryczną z obu tych przepływów:

(3)

Z empirycznej krzywej odczytujemy stan H₃ odpowiadający obliczonej wartości przepływu Q₃.

Otrzymujemy wtedy trzeci punkt o współrzędnych : Q₃ H₃

Wprowadzając określenie wartości do równania (1) otrzymujemy układ równań:

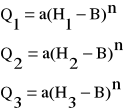
(4)

Podstawiając równanie (4) do (1) otrzymujemy :

(5)

Po podniesieniu równania (5) do kwadratu i wyciągnięciu pierwiastka stopnia n-tego otrzymujemy:

(6)

Stąd otrzymujemy :

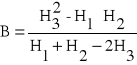
(7)

W moim przypadku:

(H_{1 ;} Q₁) (1,72 ; 0,8 )

(H_{2 ;} Q₂) (0,81 ; 0,5 )

Obliczamy średnią geometryczną Q₃ :

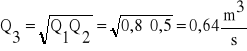
(8)

Po naniesieniu tego punktu na krzywą objętości przepływu możemy odczytać odpowiadający jej stan wody H₃ .

Otrzymujemy punkt (H_{3 ;} Q₃) o współrzędnych ( 1,26 ; 0,64)

Mając te trzy punkty możemy obliczyć wartość stałej „B”

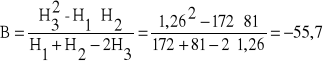
(9)

Wartość stałej „B” oraz krzywą objętości przepływu określono na podstawie tabeli zamieszczonej na stronie tematycznej ćwiczenia oraz na podstawie tabeli nr1 natomiast graficznie przedstawiono omawiane zależności na wykresie nr1 .

Q (m^3/s)	H (m)	B	T (m) T = H+B	log T	log Q
0,360	0,00	-55,70	55,70	1,7459	-0,4437
1,110	88,00	-55,70	143,70	2,1575	0,0453
0,582	146,00	-55,70	201,70	2,3047	-0,2351
0,727	170,00	-55,70	225,70	2,3535	-0,1385
1,581	195,00	-55,70	250,70	2,3992	0,1989
2,388	418,00	-55,70	473,70	2,6755	0,3780

Tabela nr 1

2. Wyznaczenie parametrów „a” i „n”

Wartości parametrów równania Harlachera wyrażające krzywą przepływu można określić graficznie i analitycznie.

W moim przypadku skorzystałam z metody graficzno-analitycznej. Wyniki zostały zamieszczone w tabeli nr2.

Q	H	T	logT	logQ
0,03	-50	5,7	0,75	-1,52
0,04	-45	10,7	1,02	-1,4
0,06	-40	15,7	1,19	-1,22
0,08	-35	20,7	1,31	-1,1
0,09	-30	25,7	1,4	-1,04
0,12	-25	30,7	1,48	-0,93
0,135	-20	35,7	1,55	-0,86
0,17	-10	45,7	1,65	-0,76
0,22	0	55,7	1,74	-0,65
0,24	10	65,7	1,81	-0,61
0,28	20	75,7	1,87	-0,55
0,315	30	85,7	1,93	-0,5
0,35	40	95,7	1,98	-0,45
0,385	50	105,7	2,02	-0,41
0,43	60	115,7	2,06	-0,36
0,46	70	125,7	2,09	-0,33
0,5	80	135,7	2,13	-0,3
0,525	90	145,7	2,16	-0,27
0,56	100	155,7	2,19	-0,25
0,59	110	165,7	2,21	-0,22
0,625	120	175,7	2,24	-0,2
0,66	130	185,7	2,26	-0,18
0,7	140	195,7	2,29	-0,15
0,73	150	205,7	2,31	-0,13
0,77	160	215,7	2,33	-0,11
0,8	170	225,7	2,35	-0,09
0,84	180	235,7	2,37	-0,07
0,885	190	245,7	2,39	-0,05
0,93	200	255,7	2,4	-0,03
0,965	210	265,7	2,42	-0,01
1	220	275,7	2,44	0
1,05	230	285,7	2,45	0,03
1,09	240	295,7	2,47	0,04
1,13	250	305,7	2,48	0,06
1,18	260	315,7	2,49	0,08
1,22	270	325,7	2,51	0,09
1,27	280	335,7	2,52	0,11
1,32	290	345,7	2,53	0,13
1,365	300	355,7	2,55	0,14
1,42	310	365,7	2,56	0,16
1,47	320	375,7	2,57	0,17
1,525	330	385,7	2,58	0,19
1,58	340	395,7	2,59	0,2
1,64	350	405,7	2,6	0,22
1,7	360	415,7	2,61	0,24
1,75	366	421,7	2,62	0,25
1,78	370	425,7	2,62	0,26
1,85	380	435,7	2,63	0,27
1,9	386	441,7	2,64	0,28
1,93	390	445,7	2,64	0,29
1,95	393	448,7	2,65	0,3
2	398	453,7	2,65	0,31
2,05	403	458,7	2,66	0,32
2,1	407	462,7	2,66	0,33
2,145	410	465,7	2,66	0,34
2,2	412	467,7	2,66	0,35
2,25	415	470,7	2,67	0,36
2,3	417	472,7	2,67	0,37
2,35	418	473,7	2,67	0,38
2,4	418	473,7	2,67	0,39

Tabela nr2

Metoda ta polega na wyrównaniu odręcznym punktów pomiarowych naniesionych na wykres w skali logarytmicznej (wykres nr.2) za pomocą linii prostej. Na tej prostej obiera się dwa punkty : początkowy i końcowy .

Logarytmując równanie (1) i podstawiając równanie (2) otrzymujemy :

(10)

Równanie prostej przechodzącej przez dwa punkty o współrzędnych (logT₁;logQ₁) i (logT₂;logQ₂) ma postać:

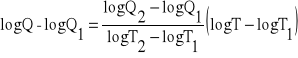
(11)

Po uporządkowaniu mamy:

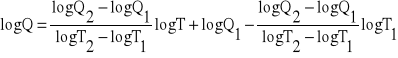
(12)

Porównując równanie (10) i (12) otrzymujemy:

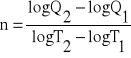
(13)

oraz:

(14)

skąd:

(15)

Podstawiając wartości liczbowe prostej I

(logQ₁;logT₁) (-1,52;0,75)

(logQ₂;logT₂) (0,39;2,67)

do wzorów otrzymuję:

(16)

Obliczone współczynniki zamieściłam w tabeli nr 3.

Prosta I	logQ1	-1,52	logT1	0,75	n=	0,99479167
	logQ2	0,39	logT2	2,67	loga=	-2,2660938
					a=	0,00541884

Tabela nr3

Współczynniki „a” i „n” dla prostej

2. Obliczanie przepływów maksymalnych rocznych na podstawie stanów maksymalnych

W zależności od parametrów a i n równanie Harlachera przyjmuje postac:

(17)

Korzystając z tych wzorów obliczam Q_max. Otrzymane wyniki zamieściłam w tabeli nr4 oraz na wykresie nr3.

m	rok	Hmax (m)	Qmax(m^3/s)	rok	Qmax(m^3/s)
1	1969	256	1,056	1975	2,322
2	1970	219	0,862	1981	2,238
3	1971	335	1,470	1989	2,040
4	1972	256	1,056	1984	2,024
5	1973	340	1,496	1995	1,961
6	1974	377	1,690	1979	1,910
7	1975	498	2,322	1988	1,841
8	1976	320	1,391	1991	1,789
9	1977	355	1,574	1987	1,758
10	1978	381,00	1,710	1978	1,710
11	1979	421	1,920	1997	1,705
12	1980	228,00	0,909	1974	1,690
13	1981	482	2,238	1986	1,627
14	1982	227	0,904	1977	1,574
15	1983	280	1,182	1973	1,496
16	1984	441	2,024	1971	1,470
17	1985	252	1,035	1976	1,391
18	1986	365	1,627	1994	1,349
19	1987	390	1,758	1993	1,276
20	1988	406,00	1,841	1983	1,182
21	1989	444	2,040	1969	1,056
22	1990	206	0,793	1972	1,056
23	1991	396	1,789	1992	1,056
24	1992	256	1,056	1996	1,051
25	1993	298	1,276	1985	1,035
26	1994	312	1,349	1980	0,909
27	1995	429	1,961	1982	0,904
28	1996	255	1,051	1970	0,862
29	1997	380	1,705	1990	0,793

Tabela nr4

Przepływy max roczne

3. Opracowanie ciągu rozdzielczego przepływów maksymalnych rocznych

Aby utworzyć ciąg rozdzielczy przepływów maksymalnych rocznych wartości maksymalnych rocznych przepływów uporządkowano od największej do najmniejszej oraz każdemu wyrazowi ciągu rozdzielczego Q_max przyporządkowano wartość prawdopodobieństwa empirycznego „empirycznego” obliczonego ze wzoru:

(18)

gdzie:

m - mty wyraz ciągu

N - ilość elementów ciągu N=29

Utworzony ciąg rozdzielczy przepływów maksymalnych rocznych oraz odpowiadające im wartości empiryczne przedstawiono w tabeli nr4.

m	Hmax (m)	Qmax(m^3/s)	P%
1	498	2,322	3,33
2	482	2,239	6,66
3	444	2,04	10
4	441	2,025	13,33
5	429	1,962	16,66
6	421	1,92	20
7	406	1,842	23,33
8	396	1,789	26,66
9	390	1,758	30
10	381	1,711	33,33
11	380	1,706	36,66
12	377	1,69	40
13	365	1,627	43,33
14	355	1,575	46,66
15	340	1,496	50
16	335	1,47	53,33
17	320	1,392	56,66
18	312	1,35	60
19	298	1,277	63,33
20	280	1,182	66,66
21	256	1,056	70
22	256	1,056	73,33
23	256	1,056	76,66
24	255	1,051	80
25	252	1,035	83,33
26	228	0,909	86,66
27	227	0,904	90
28	219	0,862	93,33
29	206	0,794	96,66

Tabela nr5

Ciąg rozdzielczy przepływów maksymalnych rocznych oraz odpowiadające mu wartości prawdopodobieństwa empirycznego.

4. Estymacja parametrów rozkładu Persona - typ III.

Po obliczeniu wyrazów ciągu rozdzielczego Q_max oraz odpowiadających mu prawdopodobieństw empirycznych wyznaczone punkty nanosimy na podziałke prawdopodobieństwa przedstawioną na wykresie nr4

Powstały w ten sposób zbiór punktów połączono odręczną krzywą tworząc empiryczna krzywą prawdopodobieństwa.

Następnie z krzywej odczytano następujące wartości:

• Q₁₀ - przepływ odpowiadający prawdopodobieństwu p=10%

• Q₅₀ przepływ odpowiadający prawdopodobieństwu p=5%

• Q₉₀- przepływ odpowiadający prawdopodobieństwu p=9%

• Q₁₀ - przepływ odpowiadający prawdopodobieństwu p=100%

gdzie:

• Q₁₀ = 2,15 m³/s

• Q₅₀ = 1,54 m³/s

• Q₉₀ = 0,91 m³/s

• Q₁₀₀ = 0,78 m³/s

Na podstawie odczytanych wartości obliczamy:

• Współczynnik zmienności „c_v” wg wzoru

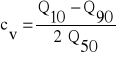
(19)

wobec tego:

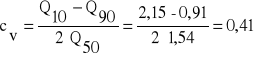
(20)

• Współczynnik skośności w funkcji wyrażenia:

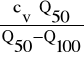
(21)

wobec tego:

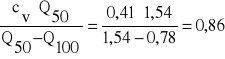
(22)

Wartość współczynnika skośności „s” odczytanego z tabeli A3 wynosi s=0,57

5. Obliczanie przepływów maksymalnych rocznych o określonym prawdopodobieństwie

Maksymalne wartości rocznych przepływów o prawdopodobieństwie od 0,1% do 100% obliczamy ze wzoru :

(23)

Wartość funkcji odczytano z tabeli A4 określającej wartość owej funkcji w zależności od współczynnika skośności s i prawdopodobieństwa.

Obliczone i odczytane wartości zamieściłam w tabeli nr5

p [ % ]	Θ ( s, p )	1+ CV * q ( s, p )	Qp
0,1	4,37	4,496	4,829
0,2	3,93	4,144	4,451
0,5	3,33	3,664	3,936
1	2,88	3,304	3,549
2	2,42	2,936	3,154
5	1,79	2,432	2,612
10	1,3	2,040	2,191
20	0,78	1,624	1,745
30	0,45	1,360	1,461
50	0	1,000	1,074
70	-0,35	0,720	0,774
80	-0,52	0,584	0,628
90	-0,7	0,440	0,473
95	-0,81	0,352	0,379
99	-0,95	0,240	0,258
100	-1,06	0,152	0,164

Tabela nr6

Wartość przepływów maksymalnych rocznych o określonym prawdopodobieństwie oraz wartości funkcji Θ(s,p)

Posiadając obliczone wartości Q_maxp nanosimy je na podziałkę prawdopodobieństwa (wykres nr4)

6. Obliczanie wartości przedziału ufności

Obliczono bezwzględną wartość największej różnicy pomiędzy prawdopodobieństwem empirycznym a teoretycznym i sprawdzamy czy spełnia warunek Kołmogorowa.

Różnica wynosi:

% (24)

gdzie:

p(m,N) - prawdopodobieństwo empiryczne m-tego wyrazu ciągu rozdzielczego [%]

p' - prawdopodobieństwo teoretyczne przepływu o wartości takiej samej, jak wyraz m ciągu rozdzielczego [%]

i jest mniejsza od wartości

(25)

Warunek
określa się testem Kołmogorowa jest spełniony można więc przyjąć rozkład prawdopodobieństwa Persona III typu jako prawidłowy.

Na skutek losowego charakteru N-letniej serii statystycznej Q_p są obarczone błędem losowym. Średni błąd oszacowania Q_p wynosi:

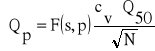
(26)

Wartość funkcji F(s,p) dla różnych wartości współczynnika skośności „s” i różnych wartości prawdopodobieństwa odczytano z tabeli A2

Prawdopodobieństwo p , że wartość Q_p znajdzie się w przedziale (
;
) nazywa się poziomem ufności a przedział nosi nazwę normalnego przedziału ufności.

Średnie błędy oszacowania
oraz granice ufności przedstawiono w tabeli nr6 oraz na wykresie nr4.

p	F(s,p)	Qmaxp	δ ( Qmaxp )		Granice przedziału ufności
%	-	m^3/s	m^3/s	m^3/s	m^3/s	m^3/s
0,1	10,324	6,518	1,648	1,648	4,87	8,166
1	5,9	4,527	0,942	0,942	3,585	5,469
5	3,183	3,152	0,508	0,508	2,644	3,66
10	2,2	2,57	0,352	0,352	2,218	2,922
50	0,978	1,276	0,157	0,157	1,119	1,433

Tabela nr6

Średnie błędy oszacowania oraz granice przedziału ufności

7. Wnioski

Wykorzystując test Kołmogorowa w zadaniu , stwierdziłam że dla danych przyjętych w ćwiczeniu można zastosować rozkład prawdopodobieństwa Persona III typu.

Odchyłka między krzywa odręczną a teoretyczną jest niewielka i mieści się w przyjętym przedziale ufności tak wiec zastosowany schemat obliczeń sprawdza się.

Wykres nr1

Krzywa konsumpcyjna

Wykres nr2

Krzywa objętości przepływu w układzie podwójnielogarytmicznym

Wykres nr3

Zależność przepływów maksymalnych rocznych na podstawie stanów maksymalnych

---