
Rys. 7.1.
7. MODELE ZACISKOWE UKŁADÓW ELEKTRYCZNCH
7.1. WIELOBIEGUNNIKI I ICH MODELE MATEMATYCZNE
Wielobiegunnikiem - zgodnie z klasyfikację elementów obwodu elektrycznego przeprowadzoną na podstawie kryterium liczby połączeń elementu z otoczeniem (liczba zacisków, końcówek, biegunów) - nazywamy element, którego liczba zacisków jest większa od 2 (m>2).
Z każdym zaciskiem wielobiegunnika związana jest para wielkości elektrycznych: Ik oraz Uk)., gdzie k oznacza kolejny numer bieguna (zacisku).
Napięcia zacisków wielobiegunnika odnosimy (określamy) względem dowolnie wybranego (nieokreślonego - w sensie niezdeterminowanego „a priorii”) zacisku odniesienia, usytuowanego w przestrzeni otaczającej wielobiegunnik. Sposób oznaczenia wielkości elektrycznych, zaciskowych m-biegunnika przedstawia rys.7.1.

Rys. 7.1.
Stan elektryczny wielobiegunnika jest jednoznacznie określony jeśli znane są wektory prądów i napięć zaciskowych definiowane w sposób następujący:
![]()
- macierz kolumnowa prądów zaciskowych (7.1)
![]()
- macierz kolumnowa napięć zaciskowych (7.2)
Postulat 1. Prądy zaciskowe każdego wielobiegunnika (traktowanego jako uogólniony węzeł elektryczny) spełniają - zgodnie z PPK - równanie:

(7.3)
Postulat 2. W każdym wielobiegunniku LINIOWYM, każdy prąd zaciskowy Ik jest funkcją liniową wszystkich napięć występujących pomiędzy wszystkimi parami zacisków wielobiegunnika, a zatem wszystkich napięć zaciskowych Ui dla i=1,2,...,m:

(7.4)
Postulat 2, w którym utożsamiono zależność funkcyjną od napięć międzyzaciskowych z zależnością od napięć zaciskowych wyjaśnia rys.7.2, na którym widnieje inny zacisk odniesienia O'. |
|
Nowy wektor napięć zaciskowych spełnia zależność:
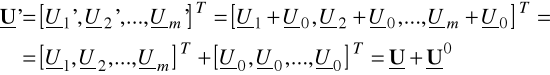
Napięcie między dowolną parą zacisków wielobiegunnika (np. między k oraz l) wyniesie:
wg rys. 7.1. Ukl=Uk-Ul
wg rys. 7.2. Ukl'=Uk'-Ul'=(Uk+U0)-(Ul+U0)=Uk-Ul=Ukl
7.2. MACIERZ ADMITANCYJNA m-biegunnika
Zakładamy, że wielobiegunnik nie jest układem zdegenerowanym, tzn. żadna para zacisków nie jest zwarta.
Drugi z postulatów sformułowanych pozwala na przedstawienie związku (7.4) w postaci m równań algebraicznych linowych:
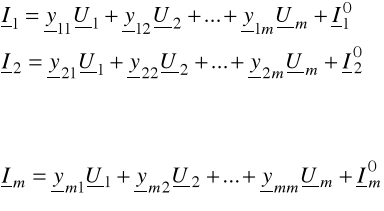
(7.5)
Gdzie prąd Ik0 nazywany prądem zerowym jest szczególnym przypadkiem prądu Ik , a mianowicie
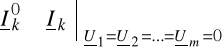
(7.6)
to znaczy, że prąd Ik0 jest prądem k-tego zacisku wielobiegunnika, gdy wszystkie zaciski wielobiegunnika są połączone bezpośrednio z węzłem odniesienia - rys.7.3.
Zatem wektor prądów zerowych
posiada, zgodnie z postulatem 1, następującą właściwość (wynikającą z (7.5), po |
|
założeniu zerowych wartości napięć zaciskowych: Uk=0, k=1,2,...,m):

(7.8)
Analizując wektor prądów zerowych można wyodrębnić dwa przypadki:
1. I0 = 0 (7.9)
Macierz prądów zerowych jest macierzą zerową, tzn. po zwarciu wszystkich zacisków wielobiegunnika wszystkie prądy zerowe przyjmują wartość zerową. Wielobiegunnik spełniający warunek (7.9) nazywamy WIELOBIEGUNNIKIEM NIEGENERUJąCYM.
Oznacza to, że w wewnętrznej strukturze wielobiegunnika nie występują nieskompensowane źródła energii i wielobiegunnik zachowuje się jak układ pasywny.
2. I0 ≠ 0 (7.10)
Macierz prądów zerowych nie jest macierzą zerową, tzn. co najmniej dwa elementy tej macierzy są różne od zera - równanie (7.8). Wielobiegunnik spełniający powyższy warunek nazywamy WIELOBIEGUNNIKIEM SAMOGENERUJąCYM.
Oznacza to, że w wewnętrznej strukturze wielobiegunnika występują nieskompensowane źródła energii i wielobiegunnik zachowuje się jak układ aktywny.
Występujące w równaniach (7.5) współczynniki ykl mają wymiar admitancji. Macierz tych współczynników (o wymiarze mm) oznaczamy symbolem Y

(7.11)
i nazywamy ADMITANCYJNą MACIERZą NIEOKREśLONą WIELOBIEGUNNIKA.
W oparciu o (7.1), (7.2), (7.7) i (7.11) można zapisać równania (7.5) w postaci macierzowej
I = YU + I0 (7.12)
dla wielobiegunnika samogenerującego, bądź uwzględniając (7.9), w postaci
I = YU (7.13)
dla wielobiegunnika niegenerującego.
Układ równań 7.5 pozwala na określenie dowolnego elementu macierzy admitancyjnej.
Np. element y11 wyniesie:
ilustruje to rys.7.4. |
|
Zatem dowolny element yij określony jest związkiem:

(7.14)
UWAGA:
suma wszystkich elementów każdej kolumny macierzy admitancyjnej nieokreślonej jest równa zeru.
suma wszystkich elementów każdego wiersza macierzy admitancyjnej nieokreślonej jest równa zeru.
7.3. CZWÓRNIKI ELEKTRYCZNE
7.3.1. WIELOBIEGUNNIK A WIELOWROTNIK I CZWÓRNIK
Definicja 1.
Jeśli: wielobiegunnik posiada parzystą liczbę zacisków (tzn. m=2n) zgrupowanych w n par
i dla każdej pary zacisków zachodzi związek
![]()
(7.15)
to: - każdą tak określoną parę zacisków nazywamy "bramą", "wrotami";
- napięcie na bramie określone jest odpowiednią różnicą napięć zaciskowych tworzących tę bramę;
- wielobiegunnik nazywamy wówczas WIELOWROTNIKIEM bądź WIELOBRAMNIKIEM.
Definicja 2.
Czwórnikiem (dwubramnikiem, dwuwrotnikiem) nazywamy wielowrotnik, dla którego 2n=4, czyli n=2.
Wyodrębnienie z klasy wielobiegunników wielowrotników a z ich zbioru czwórników ilustruje rys.7.5.

Rys.7.5.
Każdy wielowrotnik a zatem i czwórnik można opisać wektorem napięć i prądów związanych z jego wrotami i tak:
dla wielowrotnika
![]()
, ![]()
(7.16)
dla czwórnika
![]()
, ![]()
(7.17)
Przyjęte założenia pozwalają przedstawić czwórnik jak na rys.7.6.
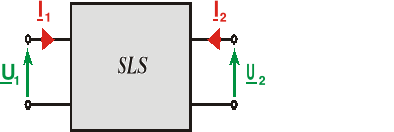
Rys.7.6.
Granicznymi stanami pracy każdej z bram są:
stan jałowy - gdy prąd danej bramy jest równy zeru
(I1=0 lub I2=0)
stan zwarcia - gdy napięcie danej bramy jest równe zeru
(U1=0 lub U2=0)
7.3.2. PODSTAWOWE RÓWNANIA CZWÓRNIKA
Równaniami czwórnika nazywamy zależności wiążące ze sobą wielkości charakteryzujące warunki jego pracy, a więc prąd i napięcie wejściowe ( I1, U1) oraz wyjściowe (I2, U2).
Ze względu na to, którą dwójkę z czterech wielkości elektrycznych wrót czwórnika przyjmiemy jako zmienne niezależne możemy sformułować sześć związków liniowych pomiędzy tymi wielkościami.
1. RÓWNANIA ADMITANCYJNE CZWÓRNIKA

(7.18)
lub w postaci macierzowej
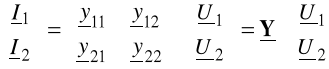
(7.19)
gdzie Y nazywamy macierzą admitancyjną czwórnika.
Model obwodowy czwórnika dla równań (7.18) przedstawia rys.7.7.

Rys.7.7.
Elementami macierzy admitancyjnej są w ogólnym przypadku liczby zespolone - można je wyznaczyć z układu równań 7.18 w granicznych stanach pracy czwórnika:


2. RÓWNANIA IMPEDANCYJNE CZWÓRNIKA

(7.20)
lub w postaci macierzowej

(7.21)
gdzie Z nazywamy macierzą impedancyjną czwórnika.
Model obwodowy czwórnika dla równań (7.20) przedstawia rys.7.8.
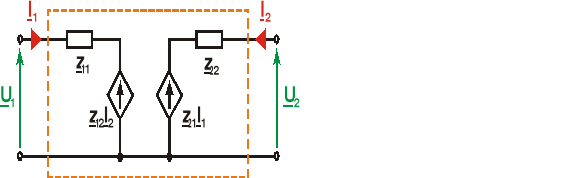
Rys.7.8.
Elementami macierzy impedancyjnej są w ogólnym przypadku liczby zespolone mające wymiar impedancji [Ω]. Można je wyznaczyć z równań 7.20 analogicznie jak poprzednio:
|
impedancja wejściowa-jałowa, tzn. impedancja "widziana" od strony bramy wejściowej przy rozwartej (stan jałowy) bramie wyjściowej. |
|
impedancja wyjściowa-jałowa, tzn. impedancja "widziana" od strony bramy wyjściowej przy rozwartej (stan jałowy) bramie wejściowej. |
|
odpowiednie transmitancje napięciowo-prądowe stanu jałowego, np.: z12- stosunek napięcia na rozwartej bramie wejściowej do prądu bramy wyjściowej, do której dołączony jest sygnał wymuszający (następuje transmisja sygnału przez czwórnik od wyjścia do wejścia). |
|
|
3. RÓWNANIA ŁAŃCUCHOWE CZWÓRNIKA
Równaniami łańcuchowymi opisujemy czwórnik wówczas, gdy znana jest para wielkości elektrycznych związanych z jedną bramą a poszukujemy wielkości elektrycznych związanych z drugą bramą.
W tym przypadku znamy [U2, I2] - wówczas równania mają postać

(7.22)
lub w postaci macierzowej
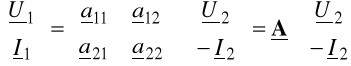
(7.23)
gdzie A nazywamy macierzą łańcuchową czwórnika, a jej elementy parametrami łańcuchowymi czwórnika.
|
Parametr bezwymiarowy będący odwrotnością transmitancji napięciowej czwórnika w stanie rozwarcia strony wtórnej. |
|
Parametr posiadający wymiar impedancji, będący odwrotnością transmitancji prądowo-napięciowej w stanie zwarcia strony wtórnej. |
|
Parametr posiadający wymiar admitancji, będący odwrotnością transmitancji napięciowo-prądowej w stanie rozwarcia strony wtórnej. |
|
Parametr bezwymiarowy będący odwrotnością transmitancji prądowej czwórnika w stanie zwarcia strony wtórnej. |
4. RÓWNANIA ŁAŃCUCHOWE ODWROTNE
Jeśli znane są wielkości [U1, I1] a poszukujemy [U2, I2], to równania typu (7.22) przyjmują postać
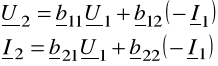
(7.24)
lub w postaci macierzowej
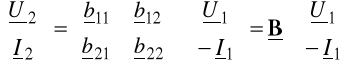
(7.25)
gdzie B nazywamy macierzą łańcuchową odwrotną czwórnika.
|
Parametr bezwymiarowy będący transmitancją napięciową czwórnika w stanie rozwarcia strony pierwotnej. |
|
Parametr posiadający wymiar impedancji, równy transmitancji napięciowo-prądowej w stanie zwarcia strony pierwotnej. |
|
Parametr posiadający wymiar admitancji, będący transmitancją prądowo-napięciową w stanie rozwarcia strony pierwotnej. |
|
Parametr bezwymiarowy równy transmitancji prądowej czwórnika w stanie zwarcia strony pierwotnej. |
5. RÓWNANIA HYBRYDOWE (szeregowo-równoległe)
Jeżeli napięcie wejściowe U1 oraz prąd wyjściowy I2 uzależnimy od I1 oraz U2, to otrzymamy równania hybrydowe czwórnika:

(7.26)
lub w postaci macierzowej
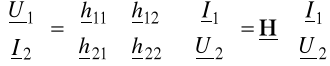
(7.27)
gdzie H nazywamy macierzą hybrydową czwórnika.
Model obwodowy czwórnika dla równań (7.26) przedstawia rys.7.9.
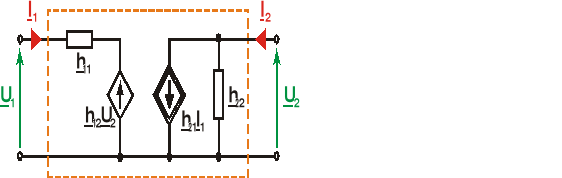
Rys.7.9.
|
Impedancja strony pierwotnej czwórnika w stanie zwarcia strony wtórnej. |
|
Parametr bezwymiarowy będący odwrotnością transmitancji napięciowej czwórnika w stanie rozwarcia strony pierwotnej. |
|
Parametr bezwymiarowy równy transmitancji prądowej czwórnika w stanie zwarcia strony wtórnej. |
|
Admitancja strony wtórnej czwórnika w stanie rozwarcia strony pierwotnej. |
6. RÓWNANIA HYBRYDOWE ODWROTNE (równoległo-szeregowe)

(7.28)
lub w postaci macierzowej

(7.29)
gdzie G nazywamy macierzą hybrydową odwrotną czwórnika.
Równaniom (7.28) odpowiada model obwodowy czwórnika przedstawiony na rys.7.10.

Rys.7.10.
|
Admitancja strony pierwotnej czwórnika w stanie rozwarcia strony wtórnej. |
|
Parametr bezwymiarowy będący odwrotnością transmitancji prądowej czwórnika w stanie zwarcia strony pierwotnej. |
|
Parametr bezwymiarowy równy transmitancji napięciowej czwórnika w stanie rozwarcia strony wtórnej. |
|
Impedancja strony wtórnej czwórnika w stanie zwarcia strony pierwotnej. |
PRZYKŁAD 1: Wyznaczyć parametry łańcuchowe czwórnika.
|
Dane: Z1=j10Ω, Z2=5Ω, Z3=j10Ω. |
Równania łańcuchowe (7.22):

Wprowadzamy ![]()
|

|
z dzielnika prądu:
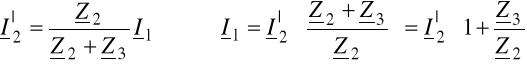


|
|
![]()
ponieważ jest to czwórnik symetryczny


- 14 -
- 15 -