Statystyka - oznacza zbiór danych dotyczących określonego zagadnienia, ogół prac związanych ze zbieraniem danych liczbowych .
Statystyka to nauka o zjawiskach ilościowych .
Zbiorowość statystyczna (populacja) to zbiór osób , przedmiotów lub zjawisk podobnych do siebie ale nie identycznych poddanych badaniu statystycznemu.
Jednostka statystyczna to każdy element zbiorowości statystycznej.
Badanie statystyczne w których bezpośredniej obserwacji podlegają wszystkie jednostki statystyczne to jednostki statystyczne pełne. Badanie statystyczne częściowe to badanie w którym bezpośredniej obserwacji podlega tylko pewien podzbiór statystyczny który nazywamy próbą. Zadaniem statystyki matematycznej jest przy wykorzystaniu metod rachunku prawdopodobieństwa wnioskowanie o całej zbiorowości statystycznej na podstawie wyników z prób. Aby na podstawie wyników z próby odnieść wnioski do całej zbiorowości próba powinna być
dostatecznie liczna
reprezentatywna tzn ze względu na badaną cechę struktura próby powinna byś zbliżona do struktury całej zbiorowości
Jednostki statystyczne mogą być wybrane do próby dwoma sposobami
przez losowanie jest to wybór przypadkowy dający każdej jednostce takież same szanse znalezienia się w próbie,
przez celową selekcję gdy jednostki do próby kwalifikuje się w sposób celowy.
Badanie statystyczne dotyczy zawsze pewnych właściwości jednostek statystycznych, które nazywamy cechami statystycznymi (cechy statystyczne zmienne podlegające badaniu) ponieważ sama typowanie jednostek do zbiorowości statystycznej wiąże się z określeniem cech które spowodują zaliczenie jednostki do danej zbiorowości. Cechy statystyczne zmienne dzielimy na :
Cechy statystyczne mierzalne (ilościowe)
Cechy statystyczne niemierzalne
AD1 Cechy statystyczne mierzalne są to takie cechy których różne warianty określane są za pomocą liczb pochodzących z pomiaru lub policzenia i wyrażone w określonych jednostkach np. wysokość dochodów, czas wykonania określonej pracy, itp. Cechy mierzalne można podzielić na dwie zasadnicze grupy:
cechy mierzalne swobodne mające skończone lub przeliczalny zbiór wartości i wartości te niezależną od dokładności pomiaru, np. liczba osób w rodzinie, liczba książek przeczytanych w ciągu roku, itp. Cechy skokowe wyrażane są w wartościach całkowitych.
Cechy mierzalne ciągłe które przyjmują wartości z pewnych przedziałów mogą być podane z różną dokładnością zależną od sposobu wykonania pomiaru np. czas wykonania pewnego detalu gdy badamy wydajność pracy, długość włókna przędzy jeśli badamy jej jakość.
Ad2 Cechy statystyczne niemierzalne to cechy których warianty opisujemy słowami które w naturalny sposób nie wyrażają się liczbami np. płeć, zawód, rodzaj ulubionej rozrywki, z pośród cech niemierzalnych wyodrębniamy cechy :
dwudzielne które mają tylko dwa warianty
cechy wielodzielne które mają tych wariantów więcej np. zawód
Z pośród cech wielodzielnych wyodrębniamy cechy, fazy mierzalne które to warianty można uporządkować według stopnia nasilenia cechy np. stan zdrowia (bardzo dobry, bardzo zły)
Cechy mierzalne
Jeżeli rozpatrujemy cechę mierzalną pewnej zbiorowości statystycznej to możemy potraktować ją jak zmienną losową i wyznaczyć jej rozkład.
Rozkład cechy w całej populacji statystycznej znamy tylko wtedy gdy przeprowadzamy badanie statystyczne pełne, gdy przeprowadzamy badanie statystyczne częściowe to znamy tylko rozkład próby tj. rozkład empiryczny. Rozkład cechy całej zbiorowości statystycznej jest znany nam przy badaniu częściowym to rozkład teoretyczny.
Przykład
Aby zbadać ile czasu tygodniowo przeznacza się w 4 osobowych rodzinach w dużych miastach Polski na prace domowe, wybrano w sposób losowy 1256 takich rodzin i dla tych rodzin wyznaczono średni czas przeznaczony na prace domowe ![]()
=10,5 h , odchylenie standardowe s=3,2 h.
Dla tego badania populacje statystyczną generalną to są wszystkie 4 osobowe rodziny dużych miast Polski, jednostką jest każda 4 osobowa rodzina. Cecha którą badamy to czas przeznaczony na prace domowa. Rodzaj cechy jest to cecha mierzalna ciągła.
Rozkład teoretyczny to rozkład zmiennej losowej która przyjmuje wartości równe wykonywania prac domowych we wszystkich tych rodzinach.
Rozkład empiryczny to rozkład tego czasu w zbadanej próbie. Zadaniem statystyki matematycznej jest wnioskowanie o tym co się dzieje we wszystkich rodzinach dużych miast Polski jeśli chodzi o czas poświęcony na prace domowe na podstawi tej liczącej 1256 elementów próby. Zadaniem statystyki matematycznej jest wnioskowanie o rozkładzie teoretycznym na podstawie znajomości rozkładu empirycznego, w ramach wnioskowania empirycznego wyróżnia się dwa zasadnicze działy.
estymacja czyli szacowanie parametrów lub postaci rozkładu teoretycznego na podstawie danych z rozkładu empirycznego
weryfikacja (testowanie) hipotez statystycznych to sprawdzanie określonych przypuszczeń dotyczących typu rozkładu teoretycznego parametrów tego rozkładu, współzależności cech, itp.
Parametry (charakterystyki liczbowe) są to takie liczby np. wartość średnia odchylenie standardowe które w sposób syntetyczny opisują nam zbiorowość statystyczną ze względu na badaną cechę.
Estymacja parametryczna
W teorii estymacji dotyczącej nieznanych parametrów rozkładu teoretycznego wyróżnia się estymację punktową i przedziałową.
Estymacja punktowa polega na znalezieniu takiej liczby która przy z góry założonej dokładności i wynikach uzyskanych z próby może być uznana za najlepszą ocenę nieznanego parametru rozkładu teoretycznego. Estymator Tn nieznanego parametru T w populacji statystycznej nazywamy taką zmienną losową której wartość obliczona na podstawie próby służy do oszacowania nieznanej wartości parametru T. Konkretną wartość liczbową
tn=t(x1 x2 x3....... xn) estymatora Tn obliczono dla wyników (x1 x2 x3..... x1) z próby nazywamy oceną parametru t.
Bardzo ważną rzeczą jest wybór estymatora dla danego parametru. W statystyce określone są własności jakie powinien posiadać ten estymator. Dla najważniejszych parametrów rozkładu teoretycznego przyjmuje się następujące estymatory. Dla wartości przeciętnej średnią arytmetyczną z próby ![]()
![]()
Dla wariacji
![]()
gdy n>30
lub ![]()
gdy m![]()
30
Odchylenie standardowe
![]()
Znacznie częściej niż estymacja punktowa stosowana jest estymacja przedziałowa. Przy tej estymacji zamiast liczbowej oceny wartości parametru podaje się pewien przedział który zawiera nieznaną wartość parametru z dużym z góry określonym prawdopodobieństwem, takie przedziały nazywamy przedziałem ufności.
Przedziałem ufności nazywamy tai przedział który z zadanym z góry prawdopodobieństwem 1-α nazywanym poziomem ufności (współczynnik ufności) zawiera nieznaną wartość szacowanego parametru. Przedziały ufności wyznacza się dla wszystkich parametrów. Najczęściej używane to : przedział ufności dla wartości przeciętnej i przedział ufności dla wskaźnika struktury.
Przedział ufności dla wartości przeciętnej.
Zakładamy że badana cecha x ma w populacji generalnej układ normalny o wartości przeciętnej m i odchyleniu standardowym σ, przedział ufności dla wartości przeciętnej m wyznaczamy z wzorów
dla próby o liczebności n>30
![]()
![]()
- średnia arytmetyczna z próby
s- odchylenie standardowe z próby
uα- znajdujemy w tablicy rozkładu
normalnego tak że φ(uα)=1-![]()
gdy próba jest mniej liczna tzn gdy n≤30 stosujemy wzór
![]()
![]()
- średnia arytmetyczna z próby
s- odchylenie standardowe z próby
![]()
- odczytujemy z tablicy rozkładu
studenta
Przykład
Oszacować metodą przedziałową tygodniowe wydatki na słodycze mieszkańców pewnego miasta na poziomie ufności 1-α=0,95 wiedząc że dla 100 losowo wybranych rodzin otrzymano średnie wydatki 12 zł przy odchyleniu standardowym s=4,72 zł.
![]()
![]()
![]()
![]()
z prawdopodobieństwem 0,95
Maksymalny błąd oszacowania przedziałowego jest równy połowie długości przedziału ufności.
![]()
Przy dużych próbach można z tego wzoru wyznaczyć n i obliczyć jak duża powinna być próba żeby wyznaczyć oszacowanie ze z góry zadaną wartością. S wyznaczamy ze wstępnej niewielkiej próby. Jest to maksymalny błąd oszacowania.
Uwagi:
przy zadanym poziomie ufności im większa jest liczebność próby tym krótszy przedział ufności
przy ustalonej liczebności próby wraz ze wzrostem poziomu ufności rośnie rozpiętość przedziału ufności (im więcej ufności tym mniej dokładności)
Przedział ufności dla wskaźnika struktury.
W badaniach statystycznych występuje często konieczność oszacowania prawdopodobieństwa występowania określonego wariantu cechy, czyli oszacowania jaki procent jednostek statystycznych ten wariant cechy posiada, czyli zachodzi konieczność oszacowania przedziałowego wskaźnika struktury.
Hipotezy Statystyczne i weryfikacyjne
Hipotezą statystyczną nazywamy każde przypuszczenie dotyczące rozkładu cechy w populacji generalnej, czyli rozkładu teoretycznego sformułowane bez przeprowadzenia badania pełnego wyłącznie na podstawie danych z próby.
Hipotezy statystyczne mogą dotyczyć parametrów nieznanego rozkładu cech w populacji generalnej, są to w tedy hipotezy parametryczne np. wartość średnia badanej cechy całej zbiorowości jest równa 5. hipotezy mogą też mówić jakiego typu jest nieznany rozkład teoretyczny, mogą dotyczyć współzależności cech badanej zbiorowości są to w tedy hipotezy nieparametryczne. Hipotezę którą sprawdzamy nazywamy hipotezą zerową i oznaczmy H0. Hipotezę alternatywną oznaczamy H1 nazywamy każdą inną hipotezę którą skłonni jesteśmy przyjąć po odrzuceniu hipotezy zerowej H0, decyzję o odrzuceniu lub przyjęciu H0 podejmujemy na podstawie wyników próby losowej .
Testem statystycznym nazywamy regułę postępowania rozstrzygającą przy jakich wynikach próby sprawdzaną hipotezęH0 należy odrzucić a przy jakich wynikach przyjąć. W czasie sprawdzania prawdziwości hipotezy H0 możliwe jest popełnienie jednego z dwóch rodzajów błędów. Błąd pierwszego rodzaju polega na odrzuceniu hipotezy H0 mimo że jest ona prawdziwa, prawdopodobieństwo popełnienia błędu pierwszego rodzaju oznaczamy symbolem i nazywamy poziomem istotności. Jako poziom istotności przyjmowane są bardzo małe liczby dodatnie np. 0,01; 0,02; 0,05; 0,1.
Błąd drugiego rodzaju polega na przyjęciu sprawdzanej hipotezy mimo że jest ona fałszywa. Prawdopodobieństwo popełnienia błędu drugiego rodzaju oznaczamy Testy przy ustalonym prawdopodobieństwie zminimalizowane jest prawdopodobieństwo popełnienia błędu drugiego rodzaju nazywane są testami najmocniejszymi. Problem popełnienia błędu drugiego rodzaju znika jeśli przy podejmowaniu decyzji bierzemy pod uwagę tylko dwie możliwości odrzucenie testowanej hipotezy H0 lub stwierdzenie że niema podstaw do odrzucenia testowanej hipotezy.
Testy parametryczne takiego typu nazywamy testami istotności wykorzystuje się je głównie do weryfikacji hipotez parametrycznych. Przy weryfikacji hipotez statystycznych stosujemy następujący schemat postępowania.
Określamy hipotezę H0 i odpowiadającą jej hipotezę H1, postać hipotezy H1 jest negacja hipotezy H0 lub jest określona przez cel badania.
Wybieramy odpowiednio do sformułowanej hipotezy H0 statystykę testową i obliczmy jej wartość na podstawie wyników z próby.
Przyjmujemy pewien poziom istotności i wyznaczamy obszar odrzucenia hipotezy H0 który nazywamy obszarem krytycznym.
Sprawdzamy czy obliczona wartość statystyki testowej należy do obszaru krytycznego, jeśli tak odrzucamy hipotezę H0 na rzecz hipotezy H1 jeśli nie stwierdzamy że niema podstaw do odrzucenia hipotezy testowanej.
Odrzucenie hipotezy H0 oznacza że różnice między wynikami badania empirycznego a sformułowaną hipotezą są statystycznie istotne, jeśli nie ma podstaw do odrzucenia hipotezy H0 uznajemy że te różnice są statystycznie nie istotne.
Test istotności dla wartości oczekiwanej.
Zakładamy że badana cecha X ma w populacji generalnej rozkład normalny o nieznanych na m parametrach m i σ, z populacji tej pobrano n elementową próbę i na podstawie tej próby obliczono średnią arytmetyczną i odchylenie standardowe.
H0: m=m0
Hipoteza H0 jest zawsze hipotezą o równości.
Dla tej hipotezy H0 możliwe są następujące hipotezy alternatywne H1
H1: mm0, albo H1: m>m0, albo H1: m<m0
W zależności od postaci hipotezy alternatywnej H1 obszar odrzucenia hipotezy będzie dwustronny, prawo stronny lub lewo stronny. Przy weryfikacji hipotez dotyczących wartości przeciętnej rozpatruje się następujące przypadki.
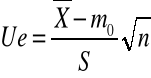
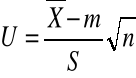
Próba liczna (n>30)
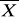
- zmienna losowa obliczana jako średnia arytmetyczna z próby
Ta statystyka ma rozkład normalny o parametrach N(0,1). Mając konkretna próbę obliczmy wartość statystyki jako
Przyjmujemy pewien poziom istotności i odrzucamy pewien obszar odrzucenia hipotezy
dwustronny obszar krytyczny
: OK.=(- , U1-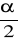
)
( U1-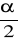
, ∝)
U1-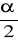
U1-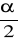
prawostronny obszar krytyczny
α: Ok.=( U1-α : ∝) φ( U1-
)=1-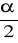
φ( U1-α)=1-α
U1-α
lewostronny obszar krytyczny
α:OK=(-∝ : U1-α)
U1-α
Sprawdzamy czy obliczona w punkcie 2 wartość empiryczna statystyki należy do obszaru krytycznego, jeśli tak to odrzucamy hipotezę H0, jeśli nie stwierdzamy że niema podstaw do odrzucenia H0
Przykład
W firmie produkującej elementy hydrauliczne badano średnią dzienną wydajność. Na podstawie wydajności w ciągu 169 dni, obliczono że średnio produkuje się 2025 szt. I odchylenie standardowe wyniosło s=20 szt. Na poziomie istotności α=0,01 zweryfikuj hipotezę że :
Średnia dzienna wydajność wynosi 2030 szt.
H1=m≠m0 m≠2030Średnia dzienna wydajność jest niższa niż 2030 szt.
H1 m<2030
![]()
AD1
α=0,01 to ![]()
to 1-![]()
0,995 wynik sprawdzamy w tablicach rozkładu normalnego i wynosi on 2,58
H1: m≠m0
m≠2030
OK=(-∝ ; - 2,58)∪(2,58 ; ∝)
-3,25 -2,58 2,58
Obliczona przez nas wartość statystyki testowej należy do obszaru krytycznego, więc testowaną hipotezę H0 odrzucamy
AD2
α=0,01 to 1-α=0,99
0,99 wynik sprawdzamy w tablicach rozkładu normalnego i wynosi on 2,33
OK =(-∝ ; - 2,33)
-3,25 -2,33
Testowaną hipotezę H0 odrzucamy ale tym razem na korzyść ... czyli średnia wydajność w tej firmie jest niższa niż 2030 szt.
Próba mała (n![]()
30)
![]()
Ta statystyka ma przy założeniu prawdziwości hipotetycznego rozkład studenta o n-1 stopniach swobody.
H0 : m≠m0
Obustronne obszar krytyczny
H1 : m≠m0 ![]()
Prawostronny obszar krytyczny
H1 : m<m0 ![]()
Lewostronny obszar krytyczny
H1 : m>m0 ![]()
![]()
Przykład 1
Tygodniowe wydatki na nabiał w 3 osobowych rodzinach mieszkających dużych miastach Polski mają rozkład normalny, przypuszcza się że średnio wydatki te są niższe od 42 zł, sprawdź czy przypuszczenie to jest słuszne jeśli 26 przebadanych rodzin uzyskano średnią arytmetyczną wydatków 44 zł i odchylenie standardowe s= 5 zł, przyjąć poziom istotności na α=0,05
H0 : m=42 zł H1 : m>42zł n=26 ![]()
=44 s=5 α=0,05
![]()
te=2
OK= (tα,n-1 ; ∝)
OK= (t2*0.05;25 : ∝)
OK= (t0.1:25 : ∝)
OK= (1,708 : ∝) 2 1,782
H0 należy odrzucić na korzyść H1 i stwierdzić że wydatki są wyższe niż 42 zł.
Przykład 2
Tygodniowe wydatki na nabiał w 3 osobowych rodzinach mieszkających dużych miastach Polski mają rozkład normalny, przypuszcza się że średnio wydatki te są niższe od 42 zł, sprawdź czy przypuszczenie to jest słuszne jeśli 26 przebadanych rodzin uzyskano średnią arytmetyczną wydatków 44 zł i odchylenie standardowe s= 5 zł, przyjąć poziom istotności na
α=0,01
OK= (t2α,n-1 ; ∝)
OK= (t2*0.01;25 : ∝)
OK= (t0.02:25 : ∝)
OK= (2,485 : ∝) 2 2,485
Na poziomie istotności 0,01 niema podstaw do odrzucenia hipotezy że tygodniowe wydatki na nabiał są równe 42 zł.
Przykład 3
Tygodniowe wydatki na nabiał w 3 osobowych rodzinach mieszkających dużych miastach Polski mają rozkład normalny, przypuszcza się że średnio wydatki te są równe 42 zł, sprawdź czy przypuszczenie to jest słuszne jeśli 26 przebadanych rodzin uzyskano średnią arytmetyczną wydatków 44 zł i odchylenie standardowe s= 5 zł, przyjąć poziom istotności na
α=0,05
H1: m≠m0
H1: m≠42 α=0,05
OK= (- ∝ ; - tα,n-1)∪(tα,n-1 ; ∝)
OK=(- ∝ : - t0,05;25)∪(t0,05;25 : ∝)
OK=(- ∝ :- 2,060) ∪(2,060 : ∝) -2,06 -2 2 2,06
Niema podstaw do odrzucenia hipotezy że przeciętne wydatki na nabiał w tych rodzinach wynoszą 42 zł na poziomie istotności 0,05
Uwaga
Jeżeli próba jest mała ale dodatkowo posiadamy informację jakie jest odchylenie standardowe rozkładu teoretycznego stosujemy I model testowania hipotezy o wartości przeciętnej czyli taki sam jak dla dużej.
Hipotezy statystyczne
Hipotezy o równości średnich w dwóch populacjach.
W zależności od liczby prób mamy kilka testów.
Zakładamy że badana cecha ma w obu populacjach rozkład normalny
I populacja N(m1σ1) n1 liczebność próby n1>30 ![]()
,s1
II populacja N(m2σ2) n2 liczebność próby n2>30 ![]()
,s2
Hipoteza H0 : m1=m2
H1 : m1≠m2 lub H1 : m1>m2 lub H1 : m1<m2
Zakładam że liczebność prób są większe niż n2>30
Na podstawie tych prób obliczono średnią dla I populacji, średnią dla II populacji, odchylenie standartowe dla I populacji i odchylenie standardowe dla II populacji. Ponieważ próby są liczne możemy przyjąć że odchylenia standardowe z próby dobrze przybliżają odchylenia standardowe z populacji.
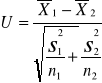
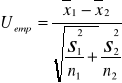
Obliczamy wartość tej statystyki i wiemy że ma ona rozkład normalny przy tym założeniu czyli dla dużych grup. Obszar krytyczny(odrzucenia hipotezy) wyznaczamy znajdując wartość krytyczną Uα z tablic rozkładu normalnego N(0,1) analogicznie jak w teście dla jednej zmiennej.
Przykład.
Badano średni czas wykonywania pewnego elementu na maszynach starego i nowego typu, otrzymano następujące dane. Maszyny nowe średni czas wykonania tego elementu wynosił ![]()
=3,6 przy odchyleniu standardowym s1=2 i liczebności n1=80, maszyny starego typu ![]()
=4,1 przy odchyleniu standardowym s2=1,8 i liczebności n2=120. Na poziomie stabilności α=0,05 zweryfikować hipotezę że średni czas wykonania elementu na maszynie nowego typu niż na maszynie starego typu.
H0 : m1=m2
H1 : m1<m2
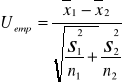
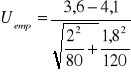
![]()
OK.=(-∝ ; -U1-α)
![]()
OK.=(-∝ ; -1,64)
![]()
-1,85 -1,64
Hipotezę o równości wartości przeciętnych należy odrzucić, czyli wydajność nowych maszyn jest lepsza.
Dla cechy nie mierzalnych stosujemy hipotezę o wskaźniku struktury.
Przykład
Przypuszcza się że ponad 60 % mieszkanek pewnego miasta nie korzysta z usług zakładu kosmetycznego. Sprawdź czy to przypuszczenie jest prawdziwe jeśli śród 500 zpytanych pań nie chodzi do kosmetyczki.
n=500 k=412 P- wskaźnik struktury kobiet nie korzystających z usług kosmetyczki
![]()
![]()
P>0,6
Hipotezę o wskaźniku struktóry testujemy zawsze na podstawie dużej próby n≥100
Hipoteza H0 : p=p0
H1 : p≠p0 lub H1 : p>p0 lub H1 : p<p0
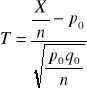
gdzie q0=1-p0
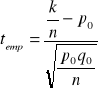
Ta statystyka ma rozkład zbliżony do normalnego a więc przy wyznaczaniu obszarów krytycznych będziemy korzystać z tablic rozkładu normalnego.
H0 : p=0,6
H1 : p>0,6
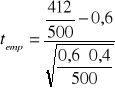
![]()
![]()
α=0,02 U1-α=2,05
OK.=(2,05 ; ∝) 2,05 10,22
Hipotezę H0 odrzucamy na poziomie istotności 0,2
Hipoteza o dwóch wskaźnikach struktury.
Porównujemy tutaj % jednostek statystycznych w dwóch populacjach mających określony wariant lub określoną wartość cechy.
Zakładamy że badana cecha ma w obu populacja rozkład dwupunktowy o prawdopodobieństwie wystąpienia wyróżnionego wariantu p1 i p2
I próba p1 n1≥100 k1- liczba elementów danego wariantu cechy.
II próba p2 n2≥100 k2- liczba elementów danego wariantu cechy.
Hipoteza 0 będzie miała postać
Hipoteza H0 : p1=p2
H1 : p1≠p2 lub H1 : p1>p2 lub H1 : p1<p2
Z obydwu tych populacji pobrano duże próby o liczebnościach co najmniej 100 elementów sprawdzianem hipotezy jest statystyka
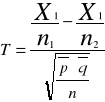
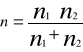
![]()
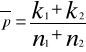
Ta statystyka jak poprzednio ma rozkład normalny i jej wartość empiryczną obliczymy za pomocą N(0,1)
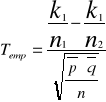
Przykład
Wysunięto hipotezę że palacze stanowią jednakowy odsetek wśród kobiet i mężczyzn, dla sprawdzenia tej hipotezy przebadano 500 mężczyzn wśród których było 200 palaczy i 600 kobiet w śród których było 250 palących papierosy na poziomie istotności α=0,05 zweryfikować daną hipotezę.
H0 p1=p2
H1 p1≠p2
![]()
![]()
n=273 ![]()
=0,41
![]()
=0,59
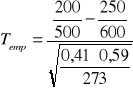
![]()
=0,975
![]()
![]()
=1,96
![]()
OK.=(-∝ ;-1,96)∪(1,96 ; ∝)
-1,96 -0,671 1,96
Niema podstaw do odrzucenia hipotezy że % palaczy wśród kobiet i mężczyzn jest taki sam.
5
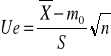
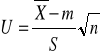
Wyszukiwarka
Podobne podstrony:
podstawowe zagadnienia statystyki 2, statystyka
podstawowe zagadnienia statystyki 4, statystyka
podstawowe zagadnienia statystyki 3, statystyka
Rodowód, przedmiot?dań i podstawowe pojęcia statystyczne Uwagi na temat organizacji?dań stat
Podstawowe pojęcia statystyki
Statystyka - podstawowe wzory, Statystyka wzory
Zagadnienia statystyczne konstruowania testów, Psychologia, biologia, Psychometria
Podstawowe pojęcia statystyki
podstawowe pojęcia statystyka, ŚCIĄGI Z RÓŻNYCH DZIEDZIN, Statystyka
zagadnienia statystyka, socjologia, skrypty i notatki, statystyka
Podstawy analizy statystycznej 2
Podstawowe pojęcia statystyczne, Statystyka - ćwiczenia - Rumiana Górska
PODSTAW WNIOSKOWANIA STATYSTYCZNEGO (Automatycznie zapisany)
Podstawowym celem statystyki jako nauki jest konstrukcja metod liczbowego opisu, Statystyka podstawy
Wyklad 4 Podstawy wnioskowania statystycznego + dodatkowe przyklady
Podstawowe pojecia statystyczne, ekonomia, logika, biznes, info
FORMY PRAWNO-ORGAN FIRM, Podstawy ekonomii, statystyki i organizacji
więcej podobnych podstron