1. Wprowadzenie

(a) Linia ograniczenia budżetowego:

p_xx + p_yy = I

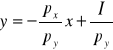
Nachylenie =

(b) Krzywe obojętności

Krańcowa stopa substytucji dobra y dobrem x(KSS)

Marginal Rate of Substitution (MRS) =
< 0, bo gdy dx>0 to dy<0.

Nachylenie =

U(x,y)

, bo jesteśmy na tej samej krzywej obojętności

- krańcowa użyteczność dobra x

- krańcowa użyteczność dobra y

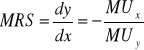
(c) Punkt optymalny

ZADANIA: 1.4.25, 1.4.27, 1.4.30

Odp.:

1.4.25: x = 65; y = 26

1.4.27: y = 10

1.4.30: owoce ↑; ryby ↓

2. Kształty krzywych obojętności

(a) Dobra substytucyjne:

(b) Dobra komplementarne:

(c) Dobra niechciane (zła):

ZADANIA: 1.4.19, 1.4.28

Odp.:

1.4.19: x = 14; y = 28

1.4.28: x(ziel.) = 10; y(czerw) = 0

3. Elastyczności

(a) Prosta cenowa elastyczność popytu:

|_D| > 1 — popyt elastyczny

|_D| < 1 — popyt nieelastyczny

|_D| = 0 — popyt sztywny

|_D| = ∞ — popyt doskonale elastyczny

_D > 0 dobra Giffena, dobra Veblena (P⇑ Q ⇑)

(b) Mieszana elastyczność cenowa popytu:

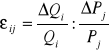
_ij > 0 — dobra substytucyjne

_ij < 0 — dobra komplementarne

(c) Elastyczność dochodowa popytu:

_I > 0 — dobra normalne (I ⇑ Q ⇑)

_I < 0 — dobra niższego rzędu (I ⇑ Q ⇓)

_I > 1 — dobra luksusowe

_I < 1 — dobra podstawowe (pierwszej potrzeby, niezbędne)

Dobra Giffena (dobra bardzo niskiego rzędu): _D > 0 i _I < 0

_D > 0 i _I >= 0 nie może istnieć

ZADANIA:

ZAD. 1: P ⇑ o 3%, Q ⇓ o 6%

Odp.: _D = -0,06 / 0,03 = -2, popyt elastyczny

ZAD. 2: Np. I ⇓ o 5%, Q ⇓ o 10%

Odp.: _I = -0,10 / -0,05 = 2, dobro normalne luksusowe

ZAD. 3: Np. P_mandarynki ⇓ o 2%, Q_pomarańcze ⇓ o 3%

Odp.: _ij = -0,03 / -0,02 = 1,5, dobra substytucyjne

4. Funkcja użyteczności Cobba-Douglasa - przykład ogólny

U(x,y) = Ax^ay^b

p.w. p_xx + p_yy = I

Ile wynosi popyt na dobro x i y i udział wydatków na oba dobra w dochodzie?

Odp.: Popyt:
,

Udziały w dochodzie:
= const.;
= const.

5. Efekt substytucyjny i dochodowy

(a) Ujęcie Słuckiego

P_x wzrost:

ES: x_S < 0 (E F)

ED: różny

x - dobro normalne:

x_S < 0

x_I < 0 (F G)

x - dobro niższego rzędu, ale nie Giffena:

x_S < 0

x_I > 0 (F H)

| x_I | < | x_S |

x - dobro Giffena:

x_S < 0

x_I > 0 (F J)

| x_I | > | x_S |

P_x spadek:

ES: x_S > 0 (E F)

ED: różny

x - dobro normalne:

x_S > 0

x_I > 0 (F G)

x - dobro niższego rzędu, ale nie Giffena:

x_S > 0

x_I < 0 (F H)

| x_I | < | x_S |

x - dobro Giffena:

x_S > 0

x_I < 0 (F J)

| x_I | > | x_S |

Tożsamość Słuckiego:

ES: x_S = x(p_x',I') - x(p_x,I)

ED: x_I = x(p_x',I) - x(p_x',I')

x = x_S + x_I = x(p_x',I') - x(p_x,I) + x(p_x',I) - x(p_x',I')

(b) Ujęcie Hicksa:

ZADANIA: 1.4.34

PYTANIA TESTOWE: 5

Odp.:

1.4.34: x=400, y=800; x' = 320, y' = 800; x_H = 360, y_H = 900, x_S = -40, x_I = ­-40

5: C

6. Nadwyżka konsumenta

RYNEK DOBRA

ZADANIA: 1.4.39

Odp.:

1.4.39: P = 5, Q = 1²/₃

7. Krzywa Engla i ścieżka wzrostu dochodu

Jak są dwa dobra, co najmniej jedno z nich musi być normalne

PYTANIA TESTOWE: 4

ZADANIE: KOT1

Odp.:

4: A

KOT1: (a) ¹/₂ - podstawowe, (b) 2 - luksusowe

8. Ekwiwalentna i kompensacyjna zmiana dochodu

ZADANIE: KOT2

Odp.:

KOT2: (a) CS = -200 ⋅ ln2 ≈ -138,6294, (b) CV = 400 ⋅ 2^1/2 - 400 ≈ 165,6854

(c) EV = 200 ⋅ 2^1/2 - 400 ≈ -117,1573

Metoda pomiaru spadku użyteczności	CV	CS	EV
Pieniężna miara spadku użyteczności	166	139	117

9. Price-consumption curve i krzywa popytu

PYTANIA TESTOWE: 9, 6, 7

Odp.:

9: B

6: C

7: D

Rysunki do pytań testowych (część teorii):

Pytanie 9

Pytanie 6:

Pytanie 7:

10. Wybór międzyokresowy

ZADANIE: 10.3

Odp.:

10.3: (a) PV = 3000, FV = 3300; (b) MRS = -c₂/c₁;

(c) -(1+r) = -1,1; -c₂/c₁ = -1,1; c₁ + c₂/1,1 = 3000 (PV) lub 1,1c₁ + c₂ = 3300 (FV);

(d) c₁ = 1500, c₂ = 1650; (e) pożyczkodawca netto, oszczędności w okresie 1 wynoszą 500

11. Rynek - podatek VAT

ZADANIE: KOT3

Odp.:

KOT3: Q = 90, P = 550; Q' = 79, P_brutto = 605, P_netto = 484; deadweight loss = 665,5; Wpływy do budżetu = 9559

KONSUMENT

1 / 12

6 / 12

9 / 12

y

x

dy

dx

y

x

dx

dy

U(x,y) - f. użyteczności

Krzywe obojętności to jej warstwice

x

y

Nachylenie l.o.b = Nachylenie krzywej ob.

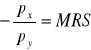
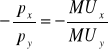
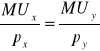
Dla n dóbr:

E

x

y

3

2

1

2 4 6

U(x,y) = x + 2y

MRS = -1/2

1

y

x

2

U(x,y) = min{2x,y}

y = 2x

y

x

Ścieżki wzrostu dochodu

y - d. luksusowe

y - dobro niechciane

wzrost U

x - d. podstawowe

_I = 1

Krzywa Engla - linia prosta

I

E

F

x - dobro normalne; Px ⇑

ES: E H

ED: H G

x

y

y

x

_I (dla dobra x) = 1; _I (dla dobra y) = 1

Ścieżka wzrostu dochodu - linia prosta

y

x

P

G

H

x - d. Giffena

x - d. niższego rzędu, ale nie Giffena

x - d. normalne

y

x

E

F

J

MRS = -2/1 = -2

MRS = -0,5/1 = -0,5

Krzywa popytu indywidualnego

Price-consumption curve

P_r-gi

Q

D

S

Nadwyżka producenta

Nadwyżka konsumenta

x

y

x

I

I1

I2

I3

I1

I2

I3

Ścieżka wzrostu dochodu

(Income-consumption curve)

Krzywa Engla

y - d. niższego rzędu

x - d. normalne

y

x

P

Q

Px₁

Px₂

Px₃

Px₁

Px₂

Px₃

D_ind

G

H

J

x

G

H

E

|_D| = 1

|_D| > 1

|_D| = nieskończoność

|_D| < 1

|_D| = 0

P_y, y, I = const. P_x∙x = const

Price∙Quantity = TR

Px↨ i TR = const |_D| = 1

Px↑ TR↑ lub Px↓ TR↓ |_D| < 1

Px↑ i TR↓ lub Px↓ TR↑ |_D| > 1

P = a/Q lub Q = a/P (a - stała)

TR = P∙Q = a = const. na całej długości

_D = ^dQ/_dP ∙ ^P/_Q = -aP^-2∙P/(a/P) = -1

Wyprowadzić _D = ^dQ/_dP ∙ ^P/_Q

Popyt elastyczny |_D| > 1

P_x↓ TR↑ P_x∙x↑

I = p_x∙x + p_y∙y

P_x∙x↑, I, p_y = const. y↓

y - d. podstawowe

Popyt nieelastyczny |_D| < 1

Rozumowanie odwrotne

PCC

x - d. luksusowe

I

x - d. luksusowe

Krzywe Engla

I

x - d. podstawowe

Ścieżki wzrostu dochodu

y - d. normalne

x - d. niższego rzędu

x

y

A

B

B

A

y

x

Zmiana kompensacyjna dochodu

(compensating variation in income)

CV = I

(taka zmiana dochodu, żeby konsument osiągnął stary poziom użyteczności przy nowych cenach)

Zmiana ekwiwalentna dochodu

(equivalent variation in income)

EV = I

(taka zmiana dochodu, żeby konsument osiągnął nowy poziom użyteczności przy starych cenach)

3000

3300

c₂

c₁

2000

1100

E

A

1650

1500

---