Zad 1

Korzystając z miar klasycznych oceń zróżnicowanie i asymetrię rozkładu temperatur……w listopadzie. Wyniki tych miar zinterpretuj

Temperatura (C^0) w listopadzie	Liczba osób…
xi	ni	xini	xi-x	(xi-x)^2	(xi-x)^2ni	Kum ni
2 3 7 13 14	4 12 8 4 2	8 36 56 52 28	-4 -3 1 7 8	16 9 1 49 64	64 108 8 196 128	4 16 24 28 30
39	30	180			504

k=5

n= 30

x=

x =

s

s

s =

s =

Int: suma temperatur w badanym okresie odchyla się przeciętnie od średniego rozkładu temperatur o 4,1

V

Int: 68% średniego rozkładu temperatur stanowi rozproszenie wokół wartości średnich temperatur o 6C^o

Me =

D=3

A

Int mamy do czynienia z asymetria silnie prawostronna

Zad 2

Zależność między liczba nieobecności x dla liczby punktów y w grupie 5 losowo wybranych studentów.

Xi	Yi	xi-x	yi -y	(xi-x)(yi-y)	(xi-x)­­^2	(yi -y)^2
1 2 3 3 6	10 8 7 6 4	-2 -1 0 0 3	3 1 0 -1 -3	-6 -1 0 0 -9	4 1 0 0 9	9 1 0 1 9
15	35			-16	14	20

a)określ siłę zależności miedzy tymi zmiennymi oraz zinterpretuj charakter tej zależności

b)oszacować liniową funkcję regresji zależność liczby punktów od liczby nieobecności y =a₁x+a_o

c)wyznacz i zinterpretuj współczynnik determinacji

r_xy =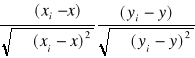

x =

x =

y=

r_xy =

W badanej próbie zachodzi silna zależność liniowa ujemna ,czyli wraz ze wzrostem liczby nieobecności zmniejsza się liczba punktów w grupie losowo wybranych studentów.

b)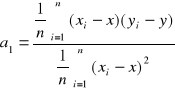

a

a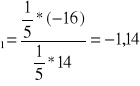

y = -1,14x+3,58

a_o = y - a

a_o=7+(-1,14)*3 = 7+(-3,42) = 7-3,42 = 3,58

Szukana prosta regresji ma postać y = -1,14x+3,58

Int: liczba nieobecnosci zalezy w 92% od liczby punktów w grupie

c) d = (r_xy)² * 100%

d = (-0,96)² * 100%

d = 0,92*100% =92%

Int:

Zad 3

Zmiany wartości produkcji (w mln zł) pewnej fabryki przedstawia tabela

Rok	97'	98'	99'	2000	2001
Wartość produkcji	2	2	4	4,2	4,4
Indeksy łańcuchowe	-	1	1,98	1,05	1,05
Indeksy o podstawie stałej (rok 2000)	0,48	0,48	0,95	1	1,05

1. wyznacz indeksy łańcuchowe ,oraz indeksy o podstawie stałej dla roku 2000

2. podaj interpretacje jednego wybranego wskaźnika łańcuchowego

3. wyznacz średnie tempo zmian oraz dokonaj interpretacji tej wielkości

b) Wartość produkcji w 2001 roku wzrosła o 5% w stosunku do roku 2000r

c)

i_g =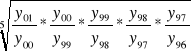

i_g =

int: zmiany wartości produktu w mln zł. Pewnej fabryki przeciętnie z roku na rok wzrosło o 34,5%

Zad 4

Informacje o wielkości obrotów pewnego sklepu listopadzie grudniu zawarte są w tabeli. Jak łącznie zmieniły się :wartość, ceny i wartości obrotów w tym sklepie? Dysponujemy dodatkowo informacja ,że łączna warość sprzedaży w grudniu roku wynosiły 260tys.zł. Zinterpretuj otrzymane wyniki.

Artykuł	Wartość obrotów (w tys.zł) w listopadzie	Zmiany cen w grudniu w stosunku do listopada
	Wit		iq	Wit: iq
A	120	wzrost o 5%	1,05	114,29
B	40	Spad 2%	0,98	40,82
C	50	Bez zmian	1	50
suma	210			205,11

I_w =

I_w =
= 1,24

260 =
_it * q_it

Int: łączna wartość sprzedaży w grudniu wzrosła o 24% w porównaniu z wartością sprzedaży w listopadzie

I
=
=
= 0,98

Int: ceny w grudniu w stosunku do listopada spadły o 2% przy założeniu że ilość sprzedaży utrzymywały się na stałym poziomie w miesiącu listopad

I
=
=
= 1,27

Int: łączna wartość obrotów w miesiącu grudzień wzrosła o 27% w stosunku do miesiąca listopad przy założeniu że ceny utrzymywały się na stałym poziomie z miesiąca grudniu

---