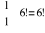Zadania dotyczące permutacji bez powtórzeń

1. Ile jest permutacji bez powtórzeń zbioru złożonego z sześciu różnych elementów?
   Odp.
   

2. Iloma sposobami można ustawić dziesięć osób w jednym rzędzie, a iloma w koło? Czy wynik ulegnie zmianie, jeżeli osoby tworzące koło zaczną się poruszać po okręgu tego koła trzymając się za ręce? (Ruch po okręgu odbywa się zgodnie z ustalonym obiegiem).
   Odp.
   

3. Ile różnych liczb czterocyfrowych można utworzyć z cyfr: l, 2,3,4 takich, aby cyfra w liczbie się nie powtarzała?
   Odp.
   

4. Ile różnych liczb pięciocyfrowych można utworzyć z cyfr: O, l, 2, 3,4 takich, aby żadne cyfry w liczbie się nie powtarzały?
   Odp.
   

5. Ile różnych liczb sześciocyfrowych można utworzyć z cyfr: 0,1,2,3,4,5 takich, aby żadna cyfra w liczbie się nie powtarzała i aby na miejscu jedności stały cyfry trzy lub cztery?
   Odp.
   

6. Podczas zawodów lekkoatletycznych w biegu na 100 m startowało siedmiu zawodników. Ile było możliwych wyników ukończenia biegu, jeżeli:

1. Wszyscy zawodnicy ukończyli bieg, Odp.
   

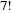
2. Jeden z zawodników nie ukończył biegu i jego nazwisko nie jest znane, Odp.
   

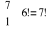
3. Jeden z zawodników nie ukończył biegu i jego nazwisko jest znane. Odp.
   

Uwaga. Zawodnicy nie dzielą miejsc ex aeąuo.

7. W urnie jest pięć kul ponumerowanych od l do 5. Losujemy ko­lejno pięć kul bez zwracania. Ile jest możliwych wyników tego lo­sowania?
   Odp.
   

8. W urnie jest pięć kul ponumerowanych od l do 5. Losujemy kolejno bez zwracania wszystkie kule i zapisujemy ich numery w ko­lejności losowania. Ile liczb pięciocyfrowych większych od dwu­dziestu tysięcy, ale mniejszych od czterdziestu tysięcy możemy otrzymać?
   Odp.
   

9. Na lekcji wychowania fizycznego nauczyciel ustawił piętnastu chłopców w rzędzie polecając im wykonywać pewne ćwiczenia ko­lejno, przy czym uczeń, który ćwiczenie już wykonał, przechodził na koniec. Zajęcie trwało tak długo, aż wszyscy chłopcy wykonali ćwiczenie, to znaczy uczeń stojący na początku ponownie znalazł się na swoim miejscu. Czy w ten sposób wyczerpano wszystkie możli­we ustawienia tych uczniów w jednym rzędzie?
   Odp. Nie
   

10. Na przystanku do autobusu wsiada grupa pasażerów składająca się z sześciu kobiet i czterech mężczyzn. Ile istnieje wszystkich możliwych realizacji wejścia pasażerów do autobusu, jeżeli pierwsze wsiadają kobiety, wszyscy wsiadają tylko tylnymi drzwiami i wsia­danie odbywa się pojedynczo?
    Odp.
    

11. W rajdzie pieszym uczestniczy grupa młodzieży składająca się z pięciu harcerek i czterech harcerzy. Maszerują w szyku zwanym „gęsiego". Ile istnieje różnych sposobów ustawienia się, jeżeli:

1. Harcerze nie mogą sąsiadować z harcerzami, a harcerki z harcer­kami, Odp.
   

2. Ustawienie w kolumnie jest dowolne. Których możliwości jest więcej? Odp.
   

12. Ile jest permutacji liczb 1,2,3,4,5,6, w których:

1. Liczby 1,2 sąsiadują ze sobą w kolejności wzrastania, Odp.
   

2. Liczby 1,2 w ogóle sąsiadują (niezależnie od kolejności), Odp.
   

3. Liczby l, 2 nie sąsiadują ze sobą, Odp.
   

4. Liczby 1,2,3 sąsiadują ze sobą w kolejności wzrastania, Odp.
   

5. Liczby 1,2,3 nie sąsiadują ze sobą. Odp.
   

13. W przedziale wagonu kolejowego ustawione są naprzeciw siebie dwie ławki mające po cztery ponumerowane miejsc od 1 do 4. Wszyst­kie siedzące miejsca w przedziale zostały zajęte. Iloma różnymi sposobami mogą usiąść pasażerowie, jeżeli wiadomo, że mogą zmie­niać miejsca tylko na ławce, na której siedzą, nie mogą natomiast zmieniać ławki?
    Odp.
    

14. Cztery kule białe, cztery czarne i cztery zielone numerujemy i układamy obok siebie w szereg tak, aby każde trzy po sobie nastę­pujące kule były różnego koloru (mp. biała, zielona, czarna). Iloma sposobami można to uczynić pod warunkiem, że kolejność barw jest ustalona?
    Odp.
    

15. Iloma sposobami można ustawić 8 wież na szachownicy tak, aby nie atakowały się wzajemnie?
    Odp.
    

16. Udowodnić metodą indukcji zupełnej, że zbiór składający się z n elementów różnych można uporządkować na n\ różnych sposobów.

Zadania dotyczące permutacji z powtórzeniami

1. Ile można utworzyć różnych wyrazów mających sens lub nie z wyrazu „baba"?
   Odp.
   

2. Ile można utworzyć różnych liczb pięciocyfrowych z liczby 11112 przestawiając jej cyfry?
   Odp.
   

3. W urnie znajduje się osiem kul ponumerowanych, przy czym 4 kule oznaczone są numerem l, dwie kule numerem 2, dwie kule numerem 3. Losujemy kolejno bez zwracania osiem kul. Ile różnych liczb ośmiocyfrowych możemy otrzymać w ten sposób?
   Odp.
   

4. Ile różnych wyrazów mających sens lub nie możemy otrzymać z wyrazu „Missisipi", przy założeniu, że wykorzystamy wszystkie litery występujące w tym wyrazie?
   Odp.
   

5. W biegu na 100 m uczestniczyło 8 zawodników. Ile jest wyników możliwych ukończenia biegu, jeżeli sędziowie punktują tylko sześć pierwszych miejsc i zawodnicy nie dzielą miejsc ex aeąuo?
   Odp.
   

6. Iloma sposobami można posadzić na pięciu krzesłach:

1. Pięć osób, Odp.
   

2. Trzy osoby. Odp.
   

7. Ile pięciocyfrowych liczb parzystych można utworzyć z cyfr l, 2,3,4 przy założeniu, że cyfra l powtarza się dwa razy?
   Odp.
   

8. Z siedmiu cyfr można utworzyć 42 liczby 7-cyfrowe. Ile cyfr jest jednakowych?
   Odp.
   

9. Ile różnych sznurów można ułożyć z sześciu korali czarnych i czterech białych przy założeniu, że ustalimy początek i koniec sznura?
   Odp. I przypadek biały….biały
   II przypadek czarny….biały
   itp. Wszystko zależy od kul, które ustalono
   

Zadania dotyczące wariacji bez powtórzeń

1. Ile różnych liczb trzycyfrowych można utworzyć z cyfr 1,2,3,4,5,6,7

1. Parzystych Odp.
   

2. Nieparzystych, Odp.
   

3. O niepowtarzających się cyfrach,? Odp.
   

2. Ile istnieje funkcji różnowartościowych określonych na zbiorze X = {1,2} o wartościach w zbiorze Y = (a, 6, c, d}? Pokazać kilka z nich za pomocą grafów.
   Odp.
   

3. Ile istnieje wariacji bez powtórzeń zbioru {a, b, c, d, e, f, g}:

1. Jednowyrazowych, Odp.
   

2. Dwuwyrazowych, Odp.
   

3. Pięciowyrazowych, Odp.
   

4. Siedmiowyrazowych. Odp.
   

4. Ile istnieje liczb pięciocyfrowych o niepowtarzających się cyf­rach?
   Odp.
   

5. Ile można utworzyć czterokolorowych chorągiewek z sześciu barw, jeżeli barwy rozumiemy jako kolorowe pasy pionowe wystę­pujące obok siebie?
   Odp.
   

6. Ile można utworzyć różnych słów sześcioliterowych z sensem lub bez dysponując alfabetem 24-literowym, w których litery nie pow­tarzają się?
   Odp.
   

7. Ile można utworzyć liczb sześciocyfrowych o niepowtarzających się cyfrach:

1. Parzystych, Odp. Zero na końcu
   + zero nie na końcu
   

2. Nieparzystych. Odp.
   

8. Ile istnieje różnych liczb czterocyfrowych o niepowtarzających się cyfrach zaczynających się od cyfry l lub 3, lub 5?
   Odp.
   

9. Punkty A, B, C, D, E, F są kolejnymi wierzchołkami sześciokąta foremnego. Ile jest wszystkich różnych różnowartościowych ciągów dwuwyrazowych o wyrazach należących do zbioru {A, B, C, D, E, F}?
   Odp.
   

10. Ile istnieje różnych liczb czterocyfrowych o niepowtarzających się cyfrach, których pierwsza cyfra jest równa, co najmniej dwa, a co najwyżej cztery?
    Odp.
    

11. W urnie znajduje się dziesięć kul ponumerowanych od l do 10. Losujemy kolejno cztery kule bez zwracania i zapisujemy ich nume­ry w kolejności losowań. Ile możemy w ten sposób wylosować liczb czterocyfrowych większych od 4000?
    Odp. Nie możemy wylosować kuli o nr 10 (bo liczba zrobi się pięciocyfrowa) więc
    

12. W ogłoszonym w 1973 roku przez Przegląd Sportowy plebiscycie na 10 najlepszych sportowców roku zgłoszono kandydatury 17 za­wodników. Plebiscyt, jak wiadomo, wygrał Ryszard Szurkowski. Obliczyć, ile istnieje sposobów przyznania dalszych miejsc zgło­szonym kandydatom. (Wykluczamy przypadek dzielenia miejsc ex aeąuo).
    Odp.
    

13. Grupa dzieci w przedszkolu bierze udział w zabawie. W jednej z faz zabawy dzieci łączą się w pary. Ile dzieci brało udział w za­bawie, jeżeli wiadomo, że mogły połączyć się w pary na 120 sposobów?
    Odp.
    

14. Z ilu osób składa się grupa, jeżeli wiadomo, że można je posadzić w trzyosobowych ławkach na sześć sposobów?
    Odp. W jednej ławce można trzy osoby posadzić na
    stąd osób musi być nie więcej niż trzy, bo 2 osoby też można usadzić na 6 sposobów, a jedną …

15. W klasie liczącej 37 uczniów rozlosowano trzy bilety jednoosobo­we do trzech różnych teatrów. Ile jest możliwych wyników losowa­nia?
    Odp.
    

16. W sali kinowej fotele ponumerowane są od l do 400, po dwa­dzieścia foteli w każdym rzędzie. Piętnastoosobowa wycieczka kupując bilety prosiła, aby były one na miejsca w rzędzie siódmym i ósmym, żeby w siódmym rzędzie otrzymało bilety dwie trzecie uczestników wycieczki i aby osoby siedzące w rzędzie ósmym nie siedziały za osobami w rzędzie siódmym. (Warunek dotyczy tylko uczestników wycieczki.) Ile istnieje sposobów kupienia biletów spełniających żądane warunki?
    Odp. Wybór 10 miejsc w rzędzie VII
    i 5 miejsc w rzędzie VIII
    spójnik „i” więc wymnażamy te liczby

17. W klasie liczącej 25 uczniów rozlosowano pięć biletów do kina opatrzonych numerami: 21, 22, 23, 24, 25. Ile istnieje wyników losowania, w których dwóch ustalonych uczniów:

1. pójdzie do kina i będzie siedzieć obok siebie,
   Odp.
   Dobieramy do tych ustalonych uczniów jeszcze trzech, a potem mieszamy tak by Ci ustaleni byli zawsze razem

2. pójdzie do kina i nie będzie siedzieć obok siebie.
   Odp.
   

18. W biegu na 100 m startuje sześciu zawodników. Ile jest możli­wych wyników ukończenia biegu, jeżeli punktowane są tylko trzy pierwsze miejsca, wszyscy zawodnicy dobiegli do mety i wykluczamy przypadek dzielenia miejsc ex aeąuo?
    Odp.
    

19. Z miasta A do miasta B prowadzi sześć dróg. Iloma sposobami można odbyć podróż A -> B -> A pod warunkiem, że nie można wracać tę samą drogą?
    Odp.
    

Zadania dotyczące wariacji z powtórzeniami

1. Mamy 8 kul numerowanych liczbami od l do 8. Kule wrzucamy na chybił trafił do 3 szuflad. Ile jest różnych rozmieszczeń tych kul?

2. Ile istnieje funkcji odwzorowujących zbiór X = {1,2,3} w zbiór Y = {a, b ,c, d, e}

3. Ile istnieje wariacji dwuwyrazowych z powtórzeniami zbioru:

1. jednoelementowego,

2. czteroelementowego,

3. w-elementowego.

4. Rzucamy:

1. dwiema,

2. trzema,

3. czterema,

4. n monetami.

Ile istnieje wszystkich możliwych wyników rzutu? (Zakładamy, że moneta jest symetryczna).

5. Rzucamy:

1. dwiema,

2. czterema,

3. pięcioma,

4. n kostkami,.

Ile istnieje wszystkich możliwych wyników rzutu?

6. Ile można utworzyć różnych liczb pięciocyfrowych z cyfr 4,5,6?

7. Ile można utworzyć różnych liczb czterocyfrowych?

8. Ile można utworzyć różnych liczb czterocyfrowych:

1. parzystych,

2. nieparzystych.

9. Ile można utworzyć różnych liczb czterocyfrowych, w których na miejscu jedności i dziesiątek występuje ta sama cyfra?

10. Na stacji kolejowej znajduje się m latarni sygnałowych. Ile róż­nych sygnałów można włączyć, jeżeli każda latarnia ma trzy świat­łą: czerwone, żółte, zielone?

11. Ile tablic rejestracyjnych możemy utworzyć dysponując alfabetem składającym się z 24 liter i cyframi l, 2,3,4,5,6,7,8,9,0?

12. Czterech studentów zdaje egzamin. Iloma sposobami mogą im być wystawione noty, jeżeli wiadomo, że żaden student nie otrzyma oceny niedostatecznej?

13. Iloma sposobami można umieścić w trzech szufladach pięć koszul?

14. Iloma sposobami można umieścić w czterech szufladach sześć koszul i pięć swetrów?

15. Z talii 52 kart losujemy jedną, zwracamy ją, karty tasujemy i lo­sujemy drugą. Ile jest możliwych wyników losowania?

16. W urnie znajduje się sześć kul ponumerowanych od l do 6. Losujemy kolejno cztery zwracając za każdym razem kulę po zapisa­niu jej numeru. Ile liczb czterocyfrowych możemy wylosować?

17. W urnie mamy dziesięć kul ponumerowanych od l do 10. Losu­jemy kolejno trzy, zwracając za każdym razem kule po zapisaniu jej numeru. Ile liczb trzycyfrowych większych, od 300, ale mniejszych od 500 możemy wylosować?

18. Alfabet Morse'a zbudowany jest z dwóch różnych elementów, kreski i kropki. Ile znaków pisarskich można utworzyć z tych ele­mentów, jeśli każdy znak nie może posiadać mniej niż 3 i więcej niż 6 miejsc oznaczonych kreskami lub kropkami?

19. W konkursie literackim jury rozpatruje dziesięć nadesłanych prac, z czego pięć najlepszych może być nagrodzonych/Ile istnieje wszy­stkich możliwości przyznania nagród niezależnie od werdyktu jury, jeżeli wiadomo, że każdą z nagród można przyznać nawet kilku au­torom równorzędnych, co do wartości prac?

Kombinacje

1. Obliczyć ilość podzbiorów zbioru:

1. pustego,

2. jednoelementowego,

3. w-elementowego.

2. Iloma sposobami można rozdzielić cztery zaproszenia na akademię między pięć osób?

3. W klasie liczącej 25 uczniów należy wybrać ośmioosobową dele­gację, która będzie reprezentowała klasę na szkolnej uroczystości. Ile istnieje sposobów wybrania tej delegacji?

4. Z okazji zjazdu koleżeńskiego spotyka się dziesięciu przyjaciół. Ile nastąpi powitań?

5. W klasie liczącej 20 chłopców należy wybrać dwie sześcioosobowe drużyny do turnieju siatkówki. Ile istnieje sposobów sformowania wspomnianych drużyn? Uwaga: Uczeń może być zawodnikiem tylko w jednej drużynie.

6. Iloma sposobami można umieścić 20 kul w trzech szufladach tak, aby w pierwszej było ich dziesięć, w drugiej sześć, a w trzeciej cztery?

7. Ile prostych można przeprowadzić przez sześć punktów, z któ­rych żadne trzy nie leżą na jednej prostej?

8. Ile płaszczyzn można przeprowadzić przez pięć punktów, z których żadne cztery nie leżą na jednej płaszczyźnie?

9. Punkty A, B, C, D, E, F, G, H są różnymi wierzchołkami wielokąta wypukłego. Obliczyć, liczbę przekątnych, które można poprowadzić w tym wielokącie?

10. W urnie znajduje się osiem kul ponumerowanych od l do 8. Losujemy trzy kule bez zwracania. Ile jest możliwych wyników lo­sowania?

11. W urnie znajduje się dziesięć kul ponumerowanych od l do 10. Losujemy trzy bez zwracania i notujemy ich numery. Ile jest możli­wych wyników losowania, w których suma wylosowanych numerów jest równa dziesięć?

12. W urnie znajduje się siedem kul ponumerowanych od l do 7. Losujemy trzy kule bez zwracania i notujemy ich numery. Ile jest możliwych wyników losowania, w których suma wylosowanych nu­merów jest liczbą nieparzystą?

13. Z talii 52 kart losujemy bez zwracania trzynaście. Ile istnieje możliwych wyników losowania?

14. Z talii 52 kart losujemy bez zwracania dziesięć. Na ile sposobów możemy wylosować asa kier?

15. Z talii 52 kart losujemy bez zwracania trzynaście. Ile istnieje możliwych wyników losowania, w których wylosujemy dwa asy?

16. Z talii 52 kart losujemy bez zwracania trzynaście. Ile istnieje możliwych wyników losowania, w których wylosujemy jednego asa, trzech króli i dwie damy?

17. Ile istnieje możliwości otrzymania przez brydżystę trzynastu kart tego samego koloru?

18. W pudełku znajduje się 20 śrub, w tym 3 wadliwie wykonane. Losujemy bez zwracania pięć śrub. Ile istnieje sposobów wylosowa­nia jednej śruby wadliwie wykonanej?

19. W pudełku znajduje się 10 żarówek, w tym trzy przepalone. Nie oglądając ich losujemy bez zwracania z pudełka cztery żarówki. Ile istnieje możliwości wylosowania samych żarówek nieprzepalonych?

20. Znaleźć liczbę wszystkich podzbiorów zbioru A = (a, b} i wy­pisać je.

---