STATYKA

1. Postulaty statyki:

1.postulat - równoległoboku - jak dodawać siły. 2 siły P₁ i P₂ dodaje się, że ich suma jest wektorem utworzonym z przekątnej równoległoboku. R=
.jeżeli mamy więcej niż dwie siły dodajemy je za pomocą wielokątów.

2.postulat -dwie siły działające na ciało sztywne pozostają w równowadze, jeśli działają wzdłuż jednej prostej i mają te same wartości i są przeciwnie skierowane - tworzą układ zerowy.

3.postulat - jeżeli na ciało działa pewien układ sił to jego działanie nie ulegnie zmianie przez dodanie lub odjęcie zerowego układu sił. Siła jest wektorem przesuwnym, można go przesuwać wzdłuż jego kierunku.

4.postulat - zesztywnienia - układ sił przyłożonych do ciała odkształcalnego nie zmienia się(jego działanie się nie zmienia) po zesztywnieniu tego ciała.

5.postulat - akcji i reakcji - każdemu działaniu towarzyszy leżące na tej samej prostej, przeciwnie skierowane i o tej samej wartości przeciwdziałanie.

6.postulat - oswobodzenie od więzów - każde ciało nieswobodne na które działa układ sił zew.-czynnych można myślowo oswobodzić od więzów zastępując ich działanie siłami reakcji więzów. Dalej rozpatrujemy ciało jako poddane działaniu sił czynnych i reakcji więzów.

2. Układy sił:

1.zbieżne - kierunki wszystkich sił przecinają się w jednym punkcie.

2.równoległe - siły są do siebie równoległe.

3.dowlone.

3. Tw. o trzech siłach:

Trzy nierównoległe do siebie siły działające w jednej płaszczyźnie pozostają w równowadze wtedy i tylko wtedy gdy tworzą układ zbierzny a ich kierunki tworzą trójkąt zamknięty.P₁=P₂+P₃.

4. Momenty sił względem punktu:

M_O=r*F

5. Moment sił względem osi:

M=P*r, moment ten jest wektorem swobodnym do płaszczyzny π- czyli ma kierunek prostej l.

6. Tw. Variniona:

Suma momentów sił układu zbieżnego względem dowolnego punktu jest równa momentowi wypadkowej tego układu względem punktu

7. Para sił:

Parą sił nazywamy układ 2 sił równoległych do siebie, równych co do wielkości, przeciwnie skierowanych P₁+P₂=0

8. Redukcja dowolnego układu płaskiego:

Redukcja układu polega na wyznaczeniu wektora głównego oraz momentu głównego R=
P_i, M₀=
M_io

9. Kratownice:

Kratownicą nazywamy układ sztywno nieważkich prętów połączonych przegubowo. Kratownica ma zastąpić ciało sztywne, kratownice obciążamy zawsze w węzłach, siły muszą działać wzdłuż pręta. Kratownica musi spełniać warunek sztywności - p=2w-3 gdzie p-ilość prętów, w-ilość węzłów. Musi być kinematycznie niezmienna. Metody rozwiązywania kratownic: węzłów-polega na rozpatrywaniu poszczególnych węzłów, Rittera-pozwala obliczyć siły w wybranych prętach.

10. Redukcja dowolnego przestrzennego układu sił:

Każdą siłę działająca na ciało sztywne możemy sprowadzić do dowolnego punktu 0 przykładając parę sił o momencie równym momentowi siły wzgl. punktu 0

R = P1 + P2 +...+ Pn = ∑ Pi ; Mo = M1o + M2o +...+ Mno =

11. Zagadnienia statycznie wyznaczalne i niewyznaczalne:

Nie można projektować kratownic aby pręty leżały w jednej linii łączone przegubowo-układ statycznie niewyznaczalny.

KINEMATYKA

1. Opis ruchu:

Aby zbadać ruch musimy to sprawdzić względem jakiegoś punktu odniesienia. Ruch jest to zmiana położenia w czasie. r-wektor położenia (początek w początku ukł. a koniec wodzi za punktem) r=xi+yj+zk. Współrzędne zmieniają się w czasie więc są funkcjami czasu x=x(t), y=y(t), z=z(t). Krzywa po której porusza się punkt jest to tor ruchu , jest to krzywa przestrzenna.

2. Prędkość:

V=lim
=
=r' , prędkość jest zawsze styczna do toru i zawsze jest wektorem. V=x'i+y'j+z'k; V=

3. Przyspieszenie:

a=lim
=r'' , przyspieszenie nigdy nie jest styczne do toru chyba że jest linią prostą. a=x''i+y''j+z''k: a=

4. Naturalny ukł. współrzędnych:

Płaszczyzna styczna do krzywej w punkcie A to każda płaszczyzna zawierającą styczną do tej krzywej w punkcie.

Płaszczyzna ściśle styczna jest to płaszczyzna do której dąży płaszczyzna styczna A₁ równoległa do stycznej do krzywej w punkcie A gdy punkt A₁ dąży do A.

Płaszczyzna normalna do stycznej w punkcie A jest to płaszczyzna zawierająca wszystkie proste prostopadłe do stycznej do tej krzywej w tym punkcie. Na przecięciu pł. normalnej i pł. stycznej leży linia normalna główna.

Płaszczyzna prostująca to pł. prostopadła do pł. normalniej pł. ściśle stycznej zawierającej punkt A.

5. Przyspieszenie styczne i normalne:

a_s =
- przyspieszenie styczne

a_n=
- przyspieszenie normalne

6. Droga:

S=

7. Kinematyczne równania ruchu:

x=x(t), y=y(t), z=z(t)

8. Prędkość w biegunowym ukł. współrzędnych:

9. Przyspieszenie w biegunowym ukł. współrzędnych:

10. Rodzaje ruchów bryły sztywnej:

1.ruch postępowy - to taki ruch w którym dowolna prosta sztywno związana z tą bryłą zajmuje położenie wzajemnie równoległe (3 stopnie swobody).

2.ruch obrotowy - to taki ruch bryły w którym dowolne dwa punkty bryły są nieruchome, prosta przechodząca przez dwa punkty to oś obrotu (1 stopień swobody).

3.ruch płaski - to taki ruch bryły w którym dowolny przekrój tej bryły płaszczyzną zajmuje położenie równoległe i jest równoległy do pewnej stałej płaszczyzny zwanej kierującą (3 stopnie swobody).

4.ruch kulisty - to taki ruch bryły w którym bryła porusza się dookoła nieruchomego punktu bryły (3 stopnie swobody).

5.ruch ogólny - jest to złożenie ruch postępowego i kulistego.

11. Ruch postępowy bryły sztywnej:

Opis ruchu bryły to opis każdego punktu bryły czyli całej bryły r_i=r_a+ρ_i

Niech prosta przechodzi przez punkty A i P.

ρ_i=const; V=
; a=
; r'_i=V_i=r'_a+0; V_i=V_a; V'_i=a_i=a_a; tory wszystkich punktów są równoległe(prędkość i przyspieszenie wszystkich punktów są jednakowe).

12. Ruch obrotowy bryły:

V_i=ω*ρ_i - prędkość punktu bryły; a_i=є*ρ_i+ω²ρ_i - przyspieszenie punktu bryły; ω=
- prędkość kątowa; є=
- przyspieszenie kątowe;

13. Ruch płaski bryły:

V=V_o+ω*r - prędkość punktu bryły; a=a_o+є*r+ω*(ω*r) - przyspieszenie punktu bryły;

Tw. o trzech rzutach - jeśli bryła znajduje się w ruchu płaskim to rzuty prędkości dwóch dowolnych punktów A i B na łączącą je proste są równe.

Taki punkt należący do bryły lub leżący poza nią który w pewnej chwili ma prędkość 0 nazywa się chwilowym środkiem obrotu (punkt C). Przy pomocy chwilowego środka obrotu możemy znaleźć prędkość punktów posługując się wzorem: V_a=ω*CA. Wektor prędkości kątowej jest zawsze taki sam i jest jeden dla wszystkich punktów bryły.

14. Ruch kulisty bryły:

V_i=ω*ρ_i

a_i=ω'*ρ_i+ω*ρ_i' są to wory w danej chwili

a_c=є*ρ_i+ω*(ω*ρ_i)

Układ Eulera jest to układ ukośny.

Precesja regularna występuje wtedy gdy ω₁=const, ω₂=const, υ'=0, ω=const

Kąt precesji ostry to precesja prosta, kąt precesji rozwarty to precesja odwrotna: ω₁+ω₂=ω

є=ω₂+ω₁=
-przyspieszenie w precesji regularnej.

15. Ruch ogólny bryły:

r_i=r_a+ρ_i x=x(t)

V_i=V_a+ω*ρ_i y=y(t)

a_i=a_a+є*ρ_i+ω*(ω*ρ_i) z=z(t)

16. Ruch złożony bryły:

Ruchem bezwzględnym punktu materialnego nazywamy ruch względem nieruchomego układu.

Ruchem względnym punktu materialnego nazywamy ruch punktu względem ruchomego układu współrzędnych.

Ruchem unoszenia punktu materialnego nazywamy ruch punktu sztywno związanego z układem ruchomym obserwowanym względem nieruchomego układu.

V_b=V_w+V_u

a_b=a_u+a_w+a_c

DYNAMIKA

1. Zasady Newtona:

I zasada bezwładności: jeżeli na punkt materialny nie działa żadna siła , lub wszystkie działające siły znasza się, to [punkt ten pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.

II zasada: jeżeli na punkt materialny o masie m działa stała siła, to punkt ten porusza się ruchem jednostajnie przyspieszonym, z przyspieszeniem wprost proporcjonalnym do działającej siły F=ma

III zasada: jeżeli ciało A działa na ciało B pewna siła, to ciało B oddziaływuje na ciało A równa co do wartości poprzedniej, posiadająca ten sam kierunek i przeciwny zwrot

2. Zasada d'Alembarta:

F+(-ma)=0; F+R+B=0, gdzie R-reakcje

Siły rzeczywiste działające na punkt równoważą się w każdej chwili z siłą bezwładności tego punktu, gdzie -ma to siła bezwładności.

3. Dynamiczne równania ruchu punktu:

4. Drgania:

Drgania swobodne - mx''= -kx; ω²=
>> x''+ω²x=0

x=Asinω_ot, gdzie x-wychylenie ciała z położenia równowagi w chwili czasu t, A-amplituda drgań, ω-częstość kołowa drgań, t-czas.

Brak tłumienia i brak wymuszenia.

Drgania tłumione - mx''+βx'+kx=0; x''+
x'+
x=0;
=2u;
=ω²

Drgania słabo tłumione (u<ω). Okres drgań jest dłuższy od okresu drgań nie tłumionych zachodzących pod działaniem takiej samej siły sprężystej. Drgania tłumione nie są drganiami periodycznymi.

Drgania silnie tłumione (u>ω) drgania tłumione są drganiami aperiodycznymi dla tych drgań wychylenie maleje wykładniczo z czasem.

Tłumienie krytyczne (u=ω).

Drgania wymuszone - mx''+kx=Hsinpt, gdzie: p-częstość kołowa siły wymuszającej, H amplituda wymuszenia; x''+
x=
sinpt; x''+ω²x=hsinpt

p<ω - wówczas przesunięcie fazowe dąży do 0 i mówimy że częstość siły wymuszającej jest zgodne w fazie z siłą wymuszającą i w tym przypadku decydujący wpływ na drgania ma siła sprężysta.

p>ω - przesunięcie fazowe dąży do -π i wychylenia drgań harmonicznych zależy od masy ciała wykonującego drgania.

p=ω - przesunięcie fazowe dąży do π/2 i zachodzi zjawisko rezonansu.

5. Pęd punktu:

p=mV - pęd

ma=F; a=
; m
=F; m=const;
(mV)=F;
=F - zasada pędu

Pochodna pędu względem czasu jest równa sumie sił działających na dany punkt.

ds=Fdt; s=
- popęd siły

Przyrost pędu punktu materialnego w skończonym przedziale czasu równy jest impulsowi siły(popędowi) działającemu na ten punkt w tym samym czasie.

Zasada zachowania pędu: jeżeli na punkt materialny nie działają żadne siły to wówczas pęd tego punktu jest wielkością stałą:
=F; F=0;
=0; p=const; mV₁=mV₂

6. Kręt punktu:

K_o=r*p=r*(mV) - kręt

=r*F - zasada krętu

Pochodna krętu punktu materialnego względem czasu jest równa momentowi wypadkowej siły działającej na punkt.

Gdy moment względem pewnego nieruchomego bieguna wypadkowej siły działających na punkt materialny wówczas kręt punktu materialnego względem wyznaczony względem tego bieguna jest stały:
=r*F; r*F=0;
=0; K₀=const

7. Praca mechaniczna:

L_ab=F ^.AB; dl=Fdr; L_ab=
F_xdx+F_ydy+F_zdz

8. Moc:

Mocą siły nazywamy pracą wykonaną w jednostce czasu. Jeśli praca siły zmienia się z czasem to wówczas moc jest pochodna pracy względem czasu: M=
[W]

9. Zasada równoważności pracy i en. kinetycznej:

Jeżeli na poruszający się punkt materialny o masie m działa siła czynna P to przyrost en. kinetycznej tego punktu jest równy pracy wykonanej przez siłę działającą na ten punkt: L=1/2mV²_k - 1/2mV²_p

10. Pole sił:

11. Pole potencjalne:

12. Siła w polu zachowawczym:

13. Potencjał i en. potencjalna:

Zdolność do wykonania pracy ciała znajdującego się w spoczynku nazywamy en. potencjalną E_p: E_p=mgh.

14. Zasada równości pracy i en. potencjalnej:

15. Zasada zachowania energii:

Podczas ruchu w polu sił ciężkości en. mechaniczna poruszającego się ciała zachowuje wartość stałą: E=E_k+E_p=const

16. Tw. o ruchu środka masy UPM:

, gdzie
-R,
=0

; Mr₀''=R

Ruch układów punktów materialnych odbywa się tak jakby cała masa układu skupiona była w jego środku masy i na który to punkt działają wszystkie siły zew.

17. Pęd układu punktów materialnych:

; Q=MV₀=
- pęd ukł. punktów materialnych;
- zasada pędu

Na pęd ma tylko wpływ siła zew, a nie wew.

R=0 >> Q=const

Jeżeli jedno ciało zyskuje pęd to drugie też go zyskuje lecz z przeciwnym znakiem.

18. Kręt ukł. punktów materialnych:

K^s=
ρ_i*mV_i - kręt

Zmiana krętu ukł. punktów mat. W czasie wywołana jest przez moment główny działający na układ brany względem nieruchomego punktu lub środka masy.

M^c=0 >> K^c=const

19. En. kinetyczna ukł. punktów mat.:

Energia kinetyczna układu punktów materialnych jest równa sumie energii kinetycznej w ruch postępowym i energii kinetycznej w ruchu względnym dookoła środka masy C układu. E =½V_cp+½ωK_c ; p=mV_c ; K_c=I_cω

27. Teoria zderzeń:

Uderzenie proste środkowe - proste-kiedy prędkość pozostaje wzdłuż jednej linii tzn. normalnej uderzenia; środkowe-kiedy w chwili uderzenia środki mas leżą na normalnej uderzenia.

V₁>V₂ ; m₁V₁+m₂V₂=m₁V₁'+m₂V₂'

Współczynnik uderzenia: k=(V₂'-V₁')/(V₁-V₂)

k=0 - uderzenie niesprężyste, k=1 - uderzenie sprężyste, 0<k<1 - uderzenie częściowo sprężyste.

Uderzenie ukośne centralne - prędkości nie są równoległe - ponieważ siła oddziaływania pomiędzy kulkami przechodzą przez środki kul czyli nie występuje siła styczna w punkcie styku, więc w kierunku stycznym pędy obu kul nie ulegną zmianie: m₁V₁=m₁V₁' ; m₂V₂=m₂V₂'

Uderzenie mimośrodowe

Hipoteza Płasona: S''=kS', gdzie k-restytucja

28. Geometria mas:

Środek masy - r_c=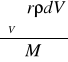

Momentem statycznym układu punktów materialnych względem dowolnego punktu O nazywamy sumę iloczynów mas tych punktów i ich promieni - wektorów S = Σ m _i r _i S = ∫ r² dm

Twierdzenie Steinera

Momet bezwładności ciała sztywnego względem dowolnej osi jest równy sumie momentu bezwładności względem osi równoległej przechodzącej przez środek masy oraz iloczynu masy ciała i kwadratu odległości między tymi dwiema osiami.

I _z' = I _z + md²

Momenty bezwładności względem punktu

I _xx =∫ x² dm

I _yy =∫ y² dm

I _zz =∫ z² dm

Momenty bezwładności względem osi:

I_x=
(y²+z²)ρdV

I_y=
(x²+z²)ρdV

I_z=
(y²+z²)ρdV

Momentem dewiacji (zboczenia) w płaszczyźnie dwóch osi układu współrzędnych karteziańskich jest całka iloczynów mas i ich odległości od płaszczyzn. Jest on zależny od rozkładu mas i kierunku osi trzeciej.

I _xy = I _yx = ∫ xy dm

I _yz = I _zy = ∫ yz dm

I _zx = I _xz = ∫ zx dm

MECHANIKA ANALITYCZNA

1. Stopnie swobody:

S=3n-k, gdzie k-ilość więzów działających na obiekt, n-ilość punktów, które w sposób jednoznaczny modelują konstrukcje.

2. Więzy:

Więzy są to ograniczenia ruch ciał.

3. Rodzaje więzów:

1.skleronomiczne lub reonomiczne (ze względu na czas),

2.geometryczne i kinematyczne (ze względu na prędkość)

3.holonomiczne i nieholonomiczne

4.jednostronne i dwustronne

5.idealne i nieidealne (ze względu na opory)

4. Współrzędne uogólnione:

q_j=q_j(t) ; j=1,...,S

5. Przesunięcie przygotowane:

Przesunięcie przygotowane(wirtualne), jego cechy:

1.nieskończenie małe

2.dowolne

3.zgodne z więzami

4.pomyślane-rzeczywiste

δr=δxi+δyj+δzk

6. Zasada prac przygotowanych:

ΔL=
(P_i+R_i)δr_i=0

Warunkiem koniecznym i wystarczającym istnienia równowagi w dowolnym układzie mechanicznym jest to aby suma prac sił czynnych i reakcji więzów na przesunięciach przygotowanych była 0.

7. Siła uogólniona:

8. Zasada prac przygotowanych w postaci uogólnionej:

9. Równowaga w polu potencjalnym:

10. Ogólne równie dynamiki analitycznej:

(F_i-mr'')δr_i=0

11. Równania Lagrango II rodzaju:

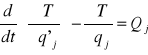
- równanie Lagrango

L=T-V - funkcja Lagrango

q' - prędkość uogólniona

---