TEMAT: Wyznaczanie momentu bezwładności i sprawdzani twierdzenia Steinera.

CEL ĆWICZENIA:

Celem ćwiczenia jest potwierdzenie zależności okresu drgań wahadła fizycznego od momentu bezwładności tego wahadła, a także wyznaczenie tego momentu bezwładności. Dodatkowym celem jest potwierdzenie teorii Steinera.

WSTĘP TEORETYCZNY:

Wahadłem fizycznym nazywamy obiekt, który wykonuje ruch drgający. Obiekt ten jest bryłą sztywną, a jej ruch daje się opisać wzorem:

gdzie: x - chwilowe wychylenie obiektu,

A - amplituda, czyli maksymalne możliwe wychylenie obiektu,

ω - pulsacja - wielkość związana z częstotliwością,

t - czas,ϕ - kąt odchylenia początkowego.

Powyższy wzór jest konsekwencją zależności:
tzn., że siła działająca na ciało jest wprost proporcjonalna do jego wychylenia i odwrotnie do niego skierowana.

Przykład wahadła fizycznego ilustruje rysunek obok. Punkt O jest punktem zawieszenia wahadła, natomiast punkt S jest jego środkiem ciężkości. Wahadło fizyczne jest bryłą sztywną. Wychylenie wahadła z położenia równowagi powoduje powstanie siły, która przeciwdziała wychyleniu. Siła ta pochodzi od przyciągania ziemskiego. Dla małych wartości kąta wychylenia wzór opisujący ruch można uprościć, ponieważ przy kątach bliskich zeru ich sinus jest w przybliżeniu funkcją liniową. Odległość d oznacza odległość pomiędzy punktem zawieszenia, a środkiem ciężkości ciała. Im odległość ta jest większa, tym drgania będą miały dłuższy okres. Jest to po prostu sformułowanie mówiące o momencie bezwładności. Poniższy wzór opisuje tę wielkość.

Jak widać zależy ona tylko od masy ciała i od kwadratu odległości. Okres drgań wahadła fizycznego wynosi:

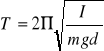
PRZEBIEG POMIARÓW:

Wszystkie niezbędne pomiary sprowadziły się w tym ćwiczeniu do zmierzenia stoperem czasu, w którym wahadło wykona 100 drgań, a także zmierzenia masy badanych ciał i odległości punktu zawieszenia od środka ciężkości. Następnie należało obliczyć moment bezwładności, dla kolejnych próbek stosując różne metody, oraz wyznaczyć stałą C.

TABELE POMIAROWE:

Dane dotyczące	Próbka	Obiekt	m [g]	Δm [g]	d[mm]	Δd [mm]
zastosowanych urządzeń	1	Tarcza	1061.6	0.01	5.06	0.01
doświadczalnych:	2	Tarcza	1061.6	0.01	10.02	0.01
	3	Tarcza	1061.6	0.01	14.97	0.01
	4	Tarcza	1061.6	0.01	12.97	0.01
	5	Pierścień	221.5	0.01
			średnica wewnętrz.		10.47	0.01
			średnica zewnętrz.		11.93	0.01

POMIARY OKRESU DRGAŃ I OBLICZENIA:

		czas 100 drgań na sekundę [s]
POMIAR	I		II	III		śr. [s]	okres 1 drgania / [s]
1	76.0		77.5	77.8		77.1	0.771
2	66.8		68.0	68.2		67.6	0.676
3	71.2		69.8	71.0		70.6	0.706
4	68.0		68.8	68.7		68.5	0.685
5	67.0		67.2	66.8		67.0	0.670

Obliczam stałą C na podstawie wzoru: (8.16 skrypt)

gdzie: T - okres drgań , d - średnica , g - 9.81

- przyjmujemy, że składowa
T nie wnosi błędu :

np. dla pomiaru 1
(0.771)²*981*5.06-4(3.14)²*(5.06)²=C

C₁ = -987.26 ΔC = 3 C = 978
3

C₂ = -3930.2 ΔC = 3 C = 3930
5

C₃ = -8704.4 ΔC = 3 C = 8704
10

C₄ = -6074.1 ΔC = 3 C = 6074
7

Obliczam moment bezwładności ciała względem osi środkowej : (8.17 skrypt)

₁ =
= -26332.9

₂ = ---- = -105793.2

₃ = ---- = -234235.4

₄ = ---- = -163454.0

Obliczam moment bezwładności pierścienia względem osi obrotu :

Korzystając ze wzoru Steinera obliczam moment bezwładności względem osi przechodzącej przez środek masy.

środek masy

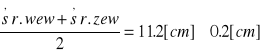
I - I₀ = ml²
I₀ = I - ml²
I₀ = 259 - 221.5 * 11.2 = - 2221.8

Obliczam moment bezwładności na podstawie wzoru tablicowego:

UWAGI I WNIOSKI:

W trakcie pomiarów czasu okresu wystąpiły dosyć duże rozbieżności przekraczające błąd bezwzględny stopera. W związku z tym za błąd bezwzględny pomiaru czasu przyjęto średnią wartość odchyłki od wartości średniej przy trzykrotnym pomiarze.

Doświadczalnie stwierdzono, że mając do dyspozycji dwa przedmioty o tej samej masie np. pierścień i tarcza większy moment bezwładności względem osi obrotu ma pierścień.

Po wykonaniu ćwiczenia na podstawie otrzymanych wyników można doświadczalnie potwierdzić tw. Steinera. wzór tablicowy jest mniej dokładny od dokładnego wzoru na obliczenie momentu bezwładności.

---