Odpowiedzi:- zjazd III

-------------------------------------------------------------------------

zad. 1.

a).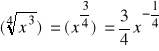
,
b)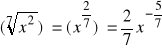
,

c).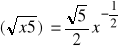
,
d).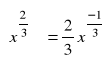
,

f).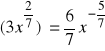
,
g).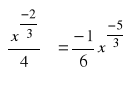
,

h).
,
i).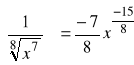
,

j).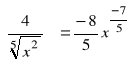
,
k).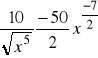
,

zad. 2.

a).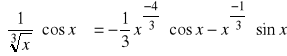
,

b).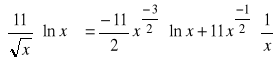
,

c).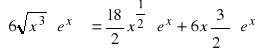
,

d). c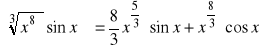
,

e).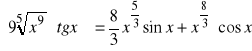
,

h).
,

i).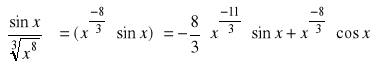
,

j).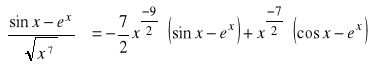
,

k).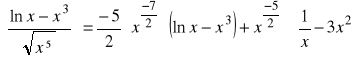
,

l).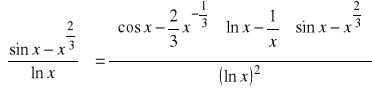

ł).
,

zad. 3.

a).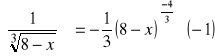
b).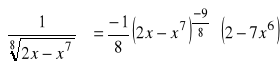

c).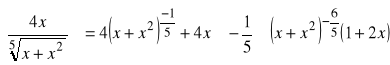

d).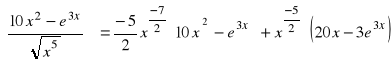

e).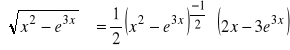
f).

g).
h).

i).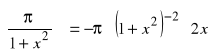
j).

k).

l).

ł).

zad. 4.

a).
; x=1;

b).
; x=0 lub x=-2

c).
; x=-1

d).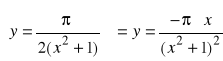
; x=0

e).
; x=0

zad.5.

Należy wyznaczyć współrzędną y₀ = f(x₀) punku styczności P(x₀ , y₀ ) , następnie zapisać rónanie stycznej w postaci :

y-y₀ = a∙(x-x₀), pamiętamy,że współczynnik kątowy prostej stycznej a = tgα = f'(x₀)

y-y₀ = f'(x₀)∙(x-x₀)

Można również znaleźć równanie stycznej wyznaczając parametr b prostej y=ax+b

podstawiajac współcrzęne punktu styczności.

a). y₀ = e^-1 , f'(x₀) = 3e

równanie stycznej y - e^-1 = 0∙(x-1) = 0 ( stczna jest równoległa do odi OX)

b), y₀ = e

y - e = 3e∙(x-1)

c). y₀ = e³

y - e³ = 2 e³ ∙(x-1)

d). y₀ = π/4

y - π/4 = -π/4 ∙(x-1)

e). y₀ = e^-1

y - e^-1 = -2 e^-1 ∙(x-1)

---