Zestaw II IŚ, zadanie 2: (granice ciągów):
a) Własności: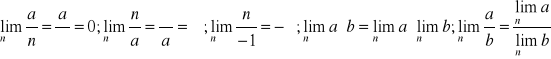
Przykłady:
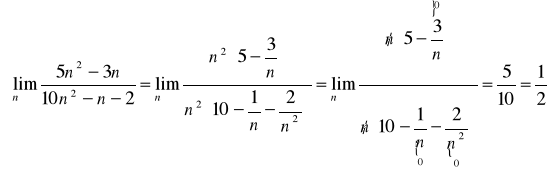
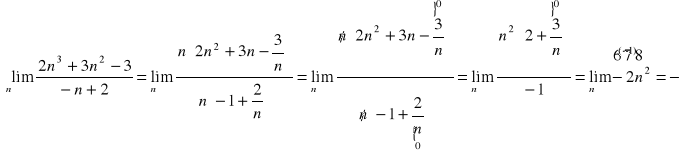
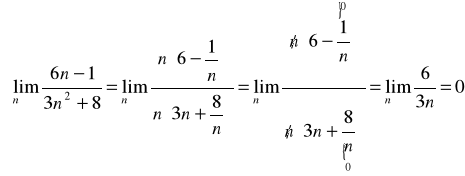
b) Własności:
![]()
Przykłady:
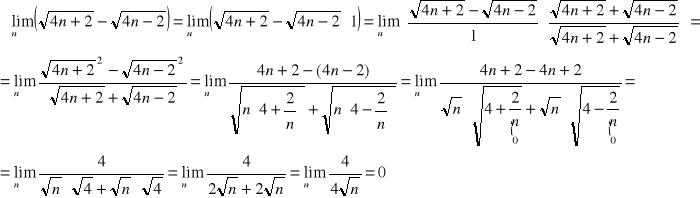
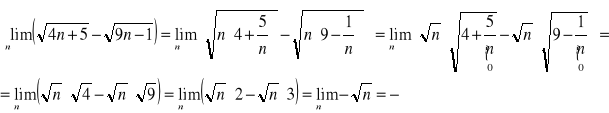

c) Własności:
![]()
Przykłady:
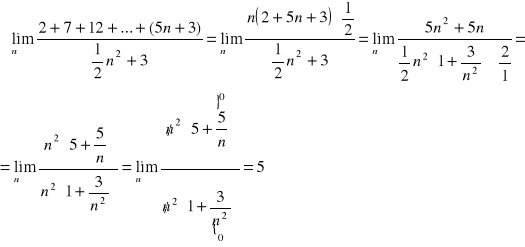
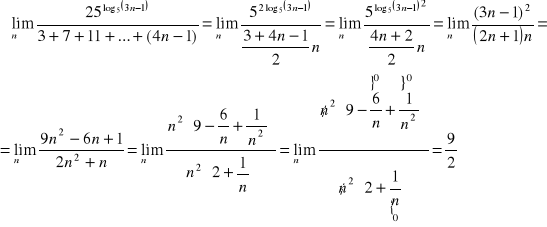
d) Własności:
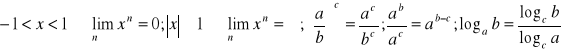
Przykłady:
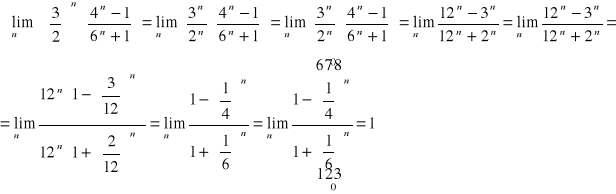
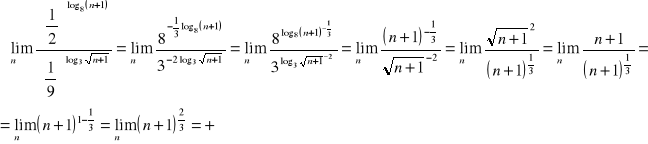
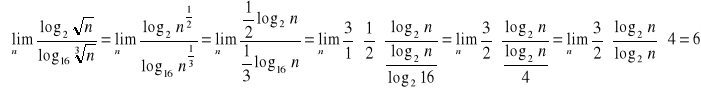
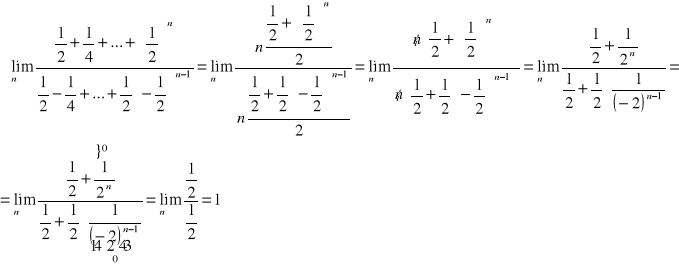
e) Przykłady:
Sposób prostszy ale nie jestem pewien czy w pełni poprawny:
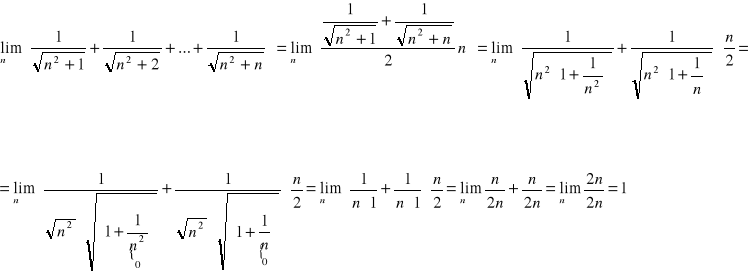
lub wykorzystujemy twierdzenie o trzech ciągach przyrównując ciągi:
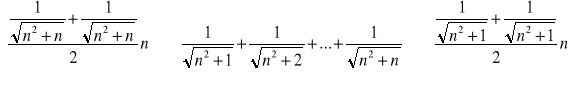
zaczynamy od obliczenia granicy ciągu większego (prawego - łatwiejszego):
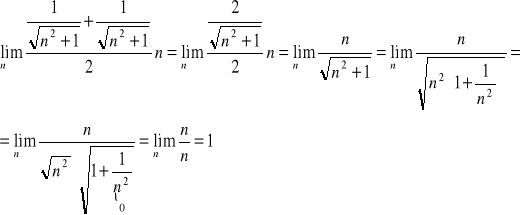
następnie obliczamy granicę ciągu mniejszego (lewego):
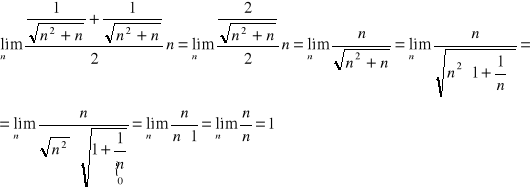
Wykorzystujemy twierdzenie o trzech ciągach:
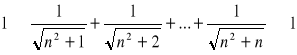
zatem granicą badanego ciągu także jest 1.
f) Przykłady:
I ponownie sposób prostszy aczkolwiek nie wiem czy do końca poprawny:
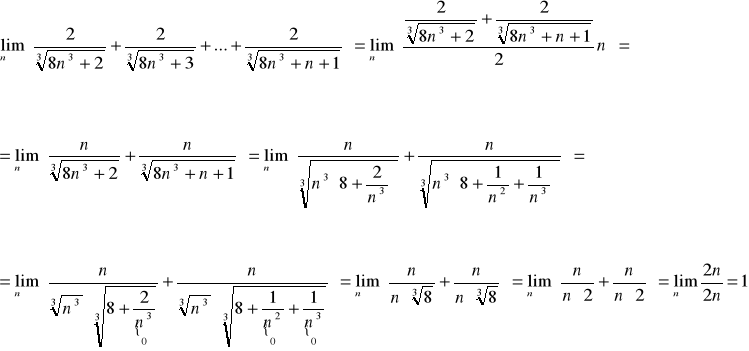
lub wykorzystujemy twierdzenie o trzech ciągach przyrównując ciągi:
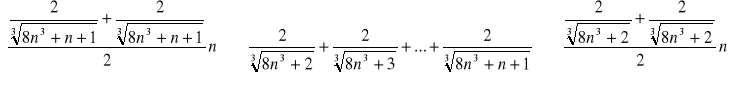
zaczynamy od obliczenia granicy ciągu większego (prawego - łatwiejszego):
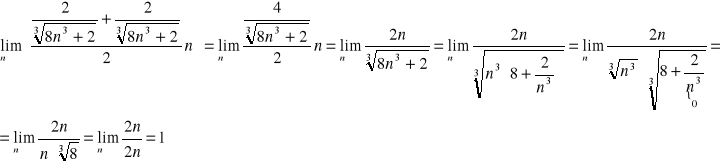
następnie obliczamy granicę ciągu mniejszego (lewego):
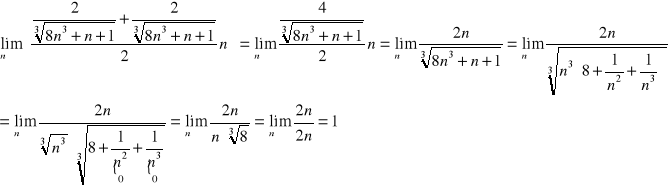
Zatem z analogicznego porównania, otrzymujemy granicę badanego ciągu równą 1.
g) Własności:
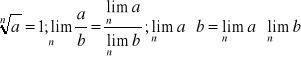
Przykłady:
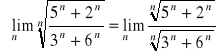
Tu już musimy wykorzystać twierdzenie o trzech ciągach
Zacznijmy od obliczenia licznika:
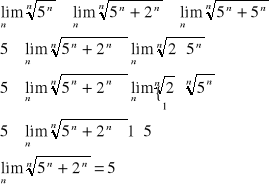
Następnie analogicznie obliczamy mianownik:
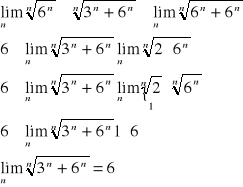
Zatem granica badanego ciągu będzie równa:
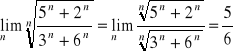
![]()
Funkcja sinusa jest funkcją ciągłą ograniczona w przedziale <-1;1> ale nie posiada granicy zatem musimy wyliczyć iloczyn granic.
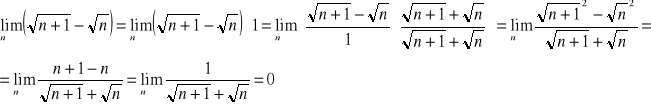
Iloczyn ciągłej funkcji sinusa i funkcji z granicą równą 0 także będzie równy 0.
Tego rozwiązania nie jestem pewien:
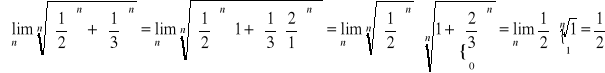
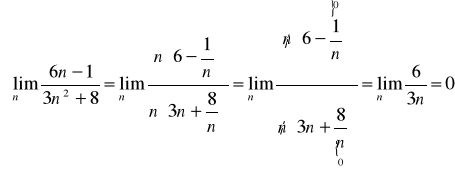
Wyszukiwarka
Podobne podstrony:
zagadanienia, ochrona środowiska UJ, I semestr, matematyka - wszystko
Uzupełnianka, ochrona środowiska UJ, V semestr, biologia roślin
Przykładowe pytania ze statystyki (1), ochrona środowiska UJ, I semestr SUM, statystyka
1-14, ochrona środowiska UJ, I semestr SUM, statystyka
Biogeografia - ściaga egzamin, ochrona środowiska UJ, I semestr SUM, biogeografia
Biogeografia - egzamin - pytania UJ, ochrona środowiska UJ, I semestr SUM, biogeografia
BIOGEOGRAFIA ściaga, ochrona środowiska UJ, I semestr SUM, biogeografia
Miniskrypt, ochrona środowiska UJ, I semestr, statystyka
epiderma, ochrona środowiska UJ, V semestr, biologia roślin
korzeń, ochrona środowiska UJ, V semestr, biologia roślin
ważne do prezentacji o nauce, ochrona środowiska UJ, I semestr SUM, podstawy dydaktyki
Chemia ogólna i nieorganiczna - zagadnienia, ochrona środowiska UJ, I semestr, chemia
Zadania specjalne, ochrona środowiska UJ, I semestr, statystyka
biogcw.ściąga, ochrona środowiska UJ, I semestr SUM, biogeografia
Biogeo.ściąga, ochrona środowiska UJ, I semestr SUM, biogeografia
Zadania, ochrona środowiska UJ, I semestr, statystyka
formy organizacyjne, ochrona środowiska UJ, I semestr SUM, dydaktyka, dydaktyka
więcej podobnych podstron