Współrzędne geograficzne
Równoleżniki: okręgi kół powstałych w wyniku przecięcia się z powierzchnią kuli płaszczyzn prostopadłych do jej osi, równoległych do płaszczyzny równika.
Południki: półokręgi powstałe w wyniku przecięcia się z powierzchnią kuli płaszczyzn przechodzących przez jej oś NS.
Dowolny punkt P na powierzchni elipsoidy można jednoznacznie wyznaczyć za pomocą kąta ၬ zwanego długością geograficzną oraz kąta ၪ zwanego szerokością geograficzną.
Długością geograficzną punktu P na kuli nazywamy kąt zawarty między płaszczyzną południka początkowego (Greenwich), a płaszczyzną południka przechodzącego przez punkt P. Za dodatnią przyjmuje się długość wschodnią. (ၬ <-180°, +180°> )
Szerokością geograficzną punktu P nazywamy kąt zawarty między płaszczyzną równika, a promieniem kuli poprowadzonym do punktu P. Za dodatnią przyjmuje się szerokość geograficzną północną. (ၪ <-90°, +90°> )
Kąt ၳ zawarty między półosią ON a promieniem kuli poprowadzonym do punktu P nazywamy odległością biegunową tego punktu.
ၳ φ
Skala główna
Przed dokonaniem odwzorowania powierzchni elipsoidy obrotowej (kuli), przyjętej jako powierzchnia oryginału, zmniejszamy ją w pewnym stałym stosunku 1 : M. Liczbę ၭ0 = 1 : M nazywamy skalą (główną) mapy. Skala główna wyraża zatem stosunek zmniejszenia wymiarów liniowych, a nie powierzchni lub objętości.
Najczęściej stosuje się skalę liczbową, np. ułamek 1:100000 oznacza, że przyjętej na mapie jednostce miary, np. 1 cm odpowiada 100000 cm, czyli 1000 m, a więc 1 km w terenie.
Oprócz skali liczbowej używa się również skali mianowanej (np. 1 cm - 1000 m, co czytamy: 1 cm na mapie odpowiada 1000 m w terenie).
Graficznym obrazem skali jest podziałka. Za pomocą podziałki można mierzyć odległości na mapie i nanosić na mapę odległości pomierzone w terenie. W przypadku map sporządzonych w małych skalach nie są możliwe pomiary za pomocą podziałki, gdyż skala znacznie różni się w różnych miejscach mapy.
Ze względu na niemożliwość otrzymania bez zniekształceń płaskiego obrazu powierzchni elipsoidy obrotowej lub powierzchni kuli przyjętej za matematyczną powierzchnię odniesienia - skala główna pozostaje zachowana tylko w tych punktach lub liniach, w których nie występują zniekształcenia długości. W pozostałych punktach i kierunkach na mapie skala główna nie może być zachowana, o czym należy pamiętać przy korzystaniu z mapy.
Skala jest stała tylko na planie, czyli obrazie niedużego wycinka powierzchni Ziemi, dla którego nie uwzględnia się krzywizny Ziemi.
Elementarna skala pól i elementarne zniekształcenie pól
(Elementarną) skalę pól w odwzorowaniu określa stosunek:
p=dP'/dP
zrealizowany przy założeniu, że skala główna ၭ0 = 1 : 1, a dP oznacza element pola na powierzchni oryginału, zaś dP' - odpowiadający mu element pola na powierzchni obrazu.
Skala długości jest funkcją dwóch zmiennych parametrycznych (U,V), a więc zależy tylko od położenia punktu na powierzchni: p = p(U,V)
Skala pól jest zawsze liczbą dodatnią i może być większa, równa lub mniejsza od jedności.
Odchylenie elementarnej skali pól od jedności - zp = p - 1 - nazywamy (elementarnym) zniekształceniem pól, które może być mniejsze, równe lub większe od zera. Niekiedy zniekształcenie pól wyraża się w procentach lub promilach.
Gdy za linie parametryczne na powierzchni oryginału i na powierzchni obrazu obierzemy siatkę krzywych głównych, wówczas wzór na elementarną skalę pól przyjmie postać: p = ab.
W ogólnym przypadku, znając elementarne skale długości w kierunku południka i równoleżnika elementarną skalę pól otrzymać możemy ze wzoru: p = mၪmၬsini = mၪmၬcosၥ ,
Gdzie i jest kątem, jaki tworzy obraz południka z obrazem równoleżnika, a ၥ jest dopełnieniem tego kąta do 90°. Te wartości można uzyskać na podstawie określonych wzorów różniczkowych.
Pojęcie krzywych głównych i kierunków głównych
Pierwsze twierdzenie Tissota o siatkach ortogonalnych:
W dowolnym regularnym odwzorowaniu jednej regularnej powierzchni na drugą istnieje zawsze przynajmniej jedna, a jeśli odwzorowanie nie jest równokątne to tylko jedna, siatka ortogonalna na powierzchni oryginału, której obraz na drugiej powierzchni będzie również siatką ortogonalną (siatka linii krzywych przecinających się pod kątami prostymi). Takie siatki nazywają się siatkami krzywych głównych.
Linie proste styczne do krzywych głównych w dowolnym punkcie powierzchni oryginału, jak również linie proste styczne do krzywych głównych w odpowiadającym temu punktowi punkcie powierzchni obrazu, nazywają się stycznymi głównymi, a ich kierunki kierunkami głównymi.
Siatki krzywych głównych i kierunki główne mają bardzo istotne znaczenie w kartografii matematycznej. Skale elementarne długości w kierunkach głównych (oznaczane przez a i b), w dowolnym punkcie odwzorowania, przyjmują wartości ekstremalne w tym punkcie, a wartości skal we wszystkich pozostałych kierunkach w tym punkcie mieszczą się w granicach wartości skal ekstremalnych. Za pomocą skal w kierunkach głównych w dowolnym punkcie odwzorowania najdogodniej można obliczyć skalę pól oraz zniekształcenia kątów występujące w tym punkcie. Wynika stąd, że badanie wartości i rozkładu zniekształceń występujących w danym odwzorowaniu sprowadza się do obliczenia wartości skal ekstremalnych w obranych punktach odwzorowania.
W kartografii, najczęściej siatkę krzywych głównych tworzy siatka równoleżników i południków geograficznego układu współrzędnych, ewentualnie (przy odwzorowaniach ukośnych) siatka almukantarantów i wertykałów azymutalnego układu współrzędnych na kuli.
Obraz siatki równoleżników i południków na mapie nosi nazwę siatki kartograficznej. W procesie redakcji map siatka ta stanowi szkielet do skonstruowania obrazu kartograficznego.
Odwzorowania azymutalne
Elipsoida lub kula odwzorowywana jest na płaszczyźnie. Równoleżniki siatki normalnej są okręgami współśrodkowymi względem obrazu bieguna Ziemi, natomiast południki - promieniami tych kręgów. Kąty między obrazami południków są równe różnicom długości geograficznych. Odstępy między obrazami równoleżników są zależne od charakteru odwzorowania i mogą być równe, wrastające lub malejące w miarę oddalania się od bieguna. Równania ogólne odwzorowań azymutalnych odpowiednio we współrzędnych biegunowych ၤ, ၲ oraz we współrzędnych prostokątnych x,y są następujące:
ၤ = ၬ; ၲ = ၲ(ၪ)
x = ၲ*cos(ၤ); y = ၲ*sin(ၤ)
Odwzorowania walcowe
Elipsoida lub kula odwzorowywana jest na pobocznicę rozpiętego na niej walca. Równoleżniki siatki normalnej są liniami prostymi wzajemnie równoległymi; południki - liniami prostymi wzajemnie równoległymi i prostopadłymi do równoleżników.Odstępy między obrazami południków są proporcjonalne do różnic długości geograficznych. Odstępy między obrazami równoleżników są zmienne, zależne od charakteru odwzorowania i mogą być równe sobie, wzrastające lub malejące w miarę oddalania się od obrazu równika. Równania ogólne we współrzędnych prostokątnych są następujące:
x = x(ၪ); y = c*ၬ, gdzie c jest stałą odwz.
Odwzorowania stożkowe
Elipsoida lub kula odwzorowywana jest na pobocznicę rozpiętego na niej stożka. Równoleżniki siatki normalnej są łukami okręgów współśrodkowych, południki zaś odcinkami prostych leżących na promieniach tych okręgów. Odstępy między obrazami południków są proporcjonalne do różnic długości geograficznych. Odstępy między obrazami równoleżników są zmienne i zależne od charakteru danego odwzorowania. Równania ogólne odwzorowań stożkowych są następujące:
ၤ = c*ၬ; ၲ = ၲ(ၪ)
x = q - ၲ*cos(ၤ); y = ၲ*sin(ၤ),
gdzie c (0 < c < 1) jest stałą odwzorowań stożkowych, zaś q oznacza odległość bieguna układu współrzędnych biegunowych od początku układu współrzędnych prostokątnych.
Odwzorowania pseudoazymutalne
Równoleżniki siatki normalnej są okręgami współśrodkowymi względem obrazu bieguna Ziemi, natomiast południki - łukami krzywych symetrycznych względem prostoliniowego obrazu południka środkowego siatki. Równania ogólne odwzorowań pseudoazymutalnych mają następującą postać:
ၤ = ၤ (ၪ,ၬ); ၲ = ၲ(ၪ)
x = ၲ*cos(ၤ); y = ၲ*sin(ၤ),
Odwzorowania pseudowalcowe
Równoleżniki siatki normalnej są (podobnie jak w odwzorowaniach walcowych) liniami prostymi wzajemnie równoległymi. Natomiast południki są na ogół liniami krzywymi, symetrycznymi względem prostoliniowego obrazu południka środkowego siatki. Bieguny Ziemi odwzorowują się na punkty lub na odcinki prostych, zależnie od warunków, jakim ma odpowiadać odwzorowanie.Równania ogólne odwzorowań pseudowalcowych są następujące:
x = x (ၪ); y = y(ၪ, ၬ
Odwzorowania pseudostożkowe
Równoleżniki siatki normalnej są w tej grupie odwzorowań łukami okręgów współśrodkowych (podobnie jak w odwzorowaniach stożkowych). Południki natomiast są łukami krzywych symetrycznie rozmieszczonych względem prostoliniowego obrazu południka środkowego siatki. Bieguny Ziemi odwzorowują się na punkty. Równania ogólne są w tym przypadku następujące:
ၤ = ၤ (ၪ,ၬ); ၲ = ၲ(ၪ)
x = q - ၲ*cos(ၤ); y = ၲ*sin(ၤ),
Symbol q oznacza odległość środka łuku obrazu równoleżnika od początku układu współrzędnych prostokątnych
Odwzorowania normalne (proste, biegunowe)
Gdy szerokość geograficzna bieguna układu współrzędnych azymutalnych ၪ0 = 90°, to wówczas wertykały i almukantaraty pokrywają się odpowiednio z południkami i równoleżnikami kuli. Siatka normalna wertykałów i almukantaratów pokrywa się z siatką normalną południków i równoleżników. Mamy wówczas odwzorowanie normalne (proste, biegunowe).
W odwzorowaniu tego typu oś biegunowa (prosta łącząca bieguny) kuli ziemskiej jest prostopadła do powierzchni odwzorowania, albo pokrywa się z osią stożka lub walca.
Odwzorowania poprzeczne (równikowe)
Gdy szerokość geograficzna bieguna układu współrzędnych azymutalnych ၪ0 = 0°, czyli biegun leży na równiku, to wówczas siatka normalna wertykałów i almukantaratów również nie pokrywa się z siatką kartograficzną południków i równoleżników. Takie odwzorowanie nazywamy poprzecznym lub równikowym.
W odwzorowaniu tego typu oś biegunowa kuli ziemskiej jest równoległa do powierzchni odwzorowania, albo prostopadła do osi stożka lub walca
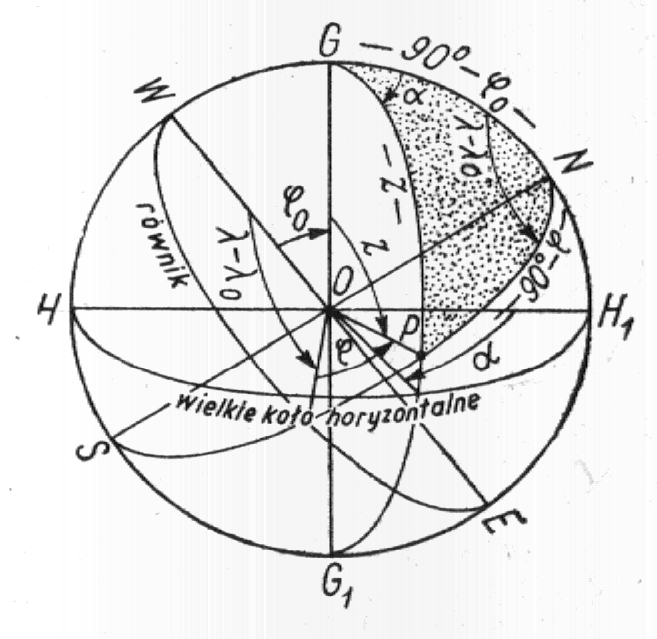
Odwzorowania ukośne (horyzontalne)
Gdy szerokość geograficzna bieguna układu współrzędnych azymutalnych 0° < ၪ0 < 90°, to wówczas siatka normalna wertykałów i almukantaratów nie pokrywa się z siatką kartograficzną południków i równoleżników. Takie odwzorowanie nazywa się ukośnym lub horyzontalnym.
W odwzorowaniu tego typu oś biegunowa kuli ziemskiej zajmuje położenie pośrednie w stosunku do położeń powyżej wymienionych
Klasyfikacja odwzorowań ze względu na sposób ich wykorzystania
Odwzorowania jednolite: Do opracowania mapy wybranego obszaru w określonym odwzorowaniu przyjmuje się jeden układ współrzędnych (najczęściej układ współrzędnych prostokątnych prostoliniowych oxy) do obliczenia siatki.
Odwzorowania wielopasmowe: Obszar podlegający odwzorowaniu dzielony jest na południkowe lub równoleżnikowe i każdy z pasów odwzorowywany jest oddzielnie. Dla każdego pasa przyjmuje się oddzielny układ współrzędnych prostokątnych prostoliniowych oxy.
Odwzorowania wielościenne: Obszar podlegający odwzorowaniu dzielony jest południkami i równoleżnikami na trapezy sferoidalne lub sferyczne odpowiedniego formatu i każdy z takich trapezów odwzorowywany jest oddzielnie, w odwzorowaniu przyjętym dla całego obszaru. Przyjmuje się tyle niezależnych układów współrzędnych prostoliniowych, na ile trapezów został podzielony dany obszar.
Odwzorowania zestawione: odwzorowania, w których siatki kartograficzne zestawiane są z siatek dwóch lub większej liczby odwzorowań.
Odwzorowania rozerwane: Odwzorowania zastosowane do przedstawienia obszarów oddzielnych części powierzchni Ziemi (mapa kontynentów lub oceanów), które łączy się ze sobą (z reguły na równiku), przy wykorzystaniu siatki rozerwanej wzdłuż odpowiednio dobranych południków. Do tego celu nadają się siatki w odwzorowaniach pseudowalcowych normalnych.
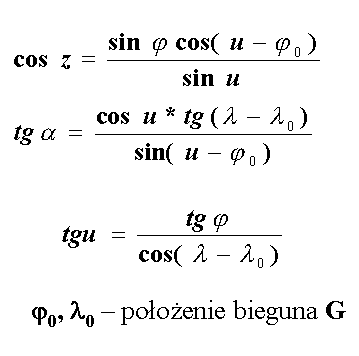
Wyszukiwarka
Podobne podstrony:
str1 2, gik, semestr 4, kartografia, Kartografia, !!! Kartografia matematyczna WOJTEK
g1, gik, semestr 4, kartografia, Kartografia, !!! Kartografia matematyczna WOJTEK, Kartografia
strona tytułowa 1, gik, semestr 4, kartografia, Kartografia, Kartografia matematyczna - powtórka z s
Kartografia matematyczna - sciaga egzamin, gik, semestr 5, Kartografia Topograficzna, KTP, kartograf
strona tytułowa 2, gik, semestr 4, kartografia, Kartografia, Kartografia matematyczna - powtórka z s
wykład2, gik, semestr 4, kartografia
wykład3, gik, semestr 4, kartografia
Wykład6, gik, semestr 4, kartografia
Wykład7, gik, semestr 4, kartografia
xxx, gik, semestr 4, kartografia, Kartografia1
PROBLEMY EGZAMINACYJNE, gik, semestr 4, kartografia, Kartografia, inne oldy
kartog, gik, semestr 5, Kartografia Topograficzna, KTP, kartografia
Karto do nauki, gik, semestr 5, Kartografia Topograficzna, KTP, kartografia
KTOcw1 moje, gik, semestr 5, Kartografia Topograficzna, KTP, kartografia
ŚCIĄGA NA EGZAMIN, gik, semestr 4, kartografia, Kartografia1
więcej podobnych podstron