Ewelina Zielińska, Agnieszka Magiera
Polaryzowalność cząsteczki - moment dipolowy
Moment dipolowy
Moment dipolowy, a dokładniej elektryczny moment dipolowy, jest to wektorowa wielkość fizyczna, która charakteryzuje dipol elektryczny. Elektryczny moment dipolowy (oznaczany literą p) dwóch ładunków punktowych o jednakowych wartościach ładunku q i przeciwnych znakach jest równy iloczynowi odległości między nimi i wartości ładunku dodatniego. Zapisujemy to w postaci równania:
p = qd,
gdzie d - wektor mający kierunek prostej łączącej ładunki q i zwrot od ładunku ujemnego do dodatniego.
Jednostką elektrycznego momentu dipolowego w układzie SI jest [ C ∙ m ]. Jednakże w fizyce atomowej i chemii stosuje się również jednostkę debaj [D].
W ćwiczeniu drugim wykonałyśmy czynności umożliwiające nam pomiar elektrycznego momentu dipolowego. Skorzystałyśmy z metody optycznej opisanej w instrukcji. Poniżej zamieszczamy kolejne czynności i obliczenia (wraz ze wzorami), które wykonywałyśmy, aby obliczyć moment dipolowy wykonanych przez nas roztworów.
1. Dane: |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||||||
numer roztworu |
waga kolbki z korkiem [g] |
waga związku polarnego z kolbką i korkiem [g] |
waga rozpuszczal- nika z kolbką [g] |
ilość związku polarnego |
ilość rozpuszczalnika |
|||||||||
|
|
|
|
[cm3] |
[g] |
[cm3] |
[g] |
|||||||
1 |
33,99 |
34,72 |
38,2 |
0,5 |
0,73 |
49,5 |
15,51 |
|||||||
2 |
30,66 |
32,92 |
37,52 |
1,5 |
2,26 |
48,5 |
17,84 |
|||||||
3 |
28,36 |
32,82 |
36,41 |
3 |
4,46 |
47 |
18,64 |
|||||||
4 |
23,27 |
30,65 |
34,85 |
5 |
7,38 |
45 |
21,73 |
|||||||
5 |
29,13 |
39,65 |
33,2 |
7 |
10,52 |
43 |
13,87 |
|||||||
6 |
23,64 |
38,5 |
30,75 |
10 |
14,86 |
40 |
16,36 |
|||||||
7 |
24,79 |
32,15 |
34,48 |
5 |
7,36 |
45 |
20,21 |
|||||||
|
|
|
|
|
|
|
|
|||||||
|
ułamek molowy związku polarnego |
C'x [pF] |
gęstość roztworu [kg/m3] |
epsilon x [pF] |
p roztworu [m3/kg] |
|
|
|||||||
1 |
|
76 |
|
0,407894737 |
|
|
|
|||||||
2 |
|
78 |
|
0,397435897 |
|
|
|
|||||||
3 |
|
79 |
|
0,392405063 |
|
|
|
|||||||
4 |
|
89,5 |
|
0,346368715 |
|
|
|
|||||||
5 |
|
84 |
|
0,369047619 |
|
|
|
|||||||
6 |
|
88 |
|
0,352272727 |
|
|
|
|||||||
7 |
|
81 |
|
0,382716049 |
|
|
|
|||||||
|
Vkolbki=50 cm3 |
|
|
|||||||||||
|
nchloroformu=1,448 |
|
|
|||||||||||
|
pusty kondensator Co=44pF |
|
||||||||||||
|
czysty cyhloheksan Ch=75pF |
|
||||||||||||
|
ni/ mi chloroformu = 0.39x1029 [C x m] lub 1,18D |
|||||||||||||
Uwaga! |
|
|
||||||||||||
POMIA 7 TO POWTÓRZENIE PRÓBY 4 |
||||||||||||||
Obliczenia
a) wyznaczanie pojemności czynnej i biernej kondensatora cieczowego.
Skorzystałyśmy ze wzorów :
Cc= |
-31,17144294 |
pF |
Pojemność czynna :![]()
Pojemność bierna : ![]()
Cb= 31pF
gdzie:
![]()
- pojemność pustego kondensatora
![]()
- pojemność kondensatora z cykloheksanem
![]()
- względna stała przenikalności elektrycznej cykloheksanu
b) wyznaczanie przenikalności elektrycznych roztworów chloroformu i cykloheksanu
Skorzystałyśmy ze wzoru:
![]()
gdzie:
![]()
- pojemność kondensatora wypełnionego roztworem x (chloroformem lub cykloheksanem)
1 |
epsilon x* |
0,407894737 |
pF |
2 |
epsilon x* |
0,397435897 |
pF |
3 |
epsilon x* |
0,392405063 |
pF |
4 |
epsilon x* |
0,346368715 |
pF |
5 |
epsilon x* |
0,369047619 |
pF |
6 |
epsilon x* |
0,352272727 |
pF |
7 |
epsilon x* |
0,382716049 |
pF |
c) obliczanie polaryzacji właściwej
Skorzystałyśmy ze wzoru: 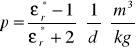
. Jednak wcześniej musiałyśmy obliczyć gęstości poszczególnych roztworów w oparciu o zasadę addytywności:
![]()
gdzie:
dcykloheksanu=![]()
dchloroformu=![]()
x - ułamek molowy
Lp. |
masa cykloheksa-nu [g] |
liczba moli cykloheksanu [mol] |
ułamek molowy cykloheksa-nu |
1 |
15,51 |
0,184642857 |
0,95504926 |
2 |
17,84 |
0,212380952 |
0,88756219 |
3 |
18,64 |
0,221904762 |
0,80692641 |
4 |
21,73 |
0,258690476 |
0,74647887 |
5 |
13,87 |
0,165119048 |
0,56867569 |
6 |
16,36 |
0,194761905 |
0,52402306 |
7 |
20,21 |
0,240595238 |
0,73304316 |
Wyniki umieściłyśmy poniżej w tabelach:
Lp. |
masa chloroformu [g] |
liczba moli chloroformu [mol] |
ułamek molowy chloroformu |
1 |
0,73 |
0,006134454 |
0,04495074 |
2 |
2,26 |
0,018991597 |
0,11243781 |
3 |
4,46 |
0,037478992 |
0,19307359 |
4 |
7,38 |
0,062016807 |
0,25352113 |
5 |
10,52 |
0,088403361 |
0,43132431 |
6 |
14,86 |
0,12487395 |
0,47597694 |
7 |
7,36 |
0,061848739 |
0,26695684 |
p1= |
-0,305325409 |
p2= |
-0,294829707 |
p3= |
-0,279465155 |
p4= |
-0,264909658 |
p5= |
-0,247735545 |
p6= |
-0,248919163 |
p7= |
-0,321389614 |
d1= |
0,80537562 |
d2= |
0,85248159 |
d3= |
0,90876537 |
d4= |
0,95095775 |
d5= |
1,07506437 |
d6= |
1,1062319 |
d7= |
0,96033587 |
d) obliczanie całkowitej polaryzacji molowej
Obliczałyśmy ją w oparciu o wzór: ![]()
gdzie:
p - polaryzacja właściwa ![]()
Mchloroformu - masa molowa chloroformu wynosząca 119,38![]()
.
P1= |
-36,33372368 |
P2= |
-35,08473519 |
P3= |
-33,25635339 |
P4= |
-31,5242493 |
P5= |
-29,48052991 |
P6= |
-29,62138035 |
P7= |
-38,24536406 |
e) obliczanie refrakcji molowej w oparciu o wzór:
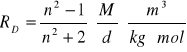
gdzie
M - masa molowa chloroformu
d - gęstość wyznaczona we wcześniejszym podpunkcie
n - współczynnik załamania światła
RD1= |
81,02292486 |
RD2= |
44,40011775 |
RD= |
41,65022612 |
RD3= |
39,80227639 |
RD4= |
39,80227639 |
RD5= |
35,20745743 |
RD6= |
34,21550488 |
RD7= |
39,41358868 |
f) obliczanie momentu dipolowego chloroformu w oparciu o wzór:
![]()
gdzie
g) rachunek błędu: błąd bezwzględny i względny
3. Porównanie momentu dipolowego chloroformu z wartością z literatury - wnioski
Wyszukiwarka
Podobne podstrony:
sprawozdanie moment dipolowy, fizyczna, chemia fizyczna, Fizyczna, laborki
moment dipolowy poprawa 03.12.11 bw, fizyczna, chemia fizyczna, Fizyczna, laborki
Pojęcia na egzamin z metali, Chemia Fizyczna, chemia fizyczna- laborki rozne, Rozne
mmgg, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna cz II sprawka
Ćwiczenie 1 - oznaczanie stalej i stopnia dysocjacji, Biotechnologia PWR, Semestr 3, Chemia fizyczna
Korelacja liniowa, fizyczna, chemia fizyczna, Fizyczna, CH. FIZYCZNA, laborki sprawozdania fizyczna
Fizyczna ćw 4, fizyczna, chemia fizyczna, Fizyczna, CH. FIZYCZNA, laborki sprawozdania fizyczna
ogniwa galwaniczne, fizyczna, chemia fizyczna, Fizyczna, laborki
spr57, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy
Moje 50 , Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna cz II spr
monia 11, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna cz II spr
15 wyznaczanie ciepła spalania, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, Chem
Chemia a ochrona środowiska - referat, Chemia Fizyczna, chemia fizyczna- laborki rozne, Rozne
Dane, fizyczna, chemia fizyczna, Fizyczna, CH. FIZYCZNA, laborki sprawozdania fizyczna
teoria 1, fizyczna, chemia fizyczna, Fizyczna, laborki
KOND41vmac, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna cz II s
Katalizatory - referat, Chemia Fizyczna, chemia fizyczna- laborki rozne, Rozne
więcej podobnych podstron