POLITECHNIKA POZNAŃSKA Rok Akademicki 2008/2009

Wydział Budownictwa i Inżynierii Środowiska Semestr 4

Instytut Konstrukcji Budowlanych

Zakład Konstrukcji Żelbetowych

Ćwiczenia Projektowe z

Konstrukcji Żelbetowych

Prowadzący: dr inż. Jerzy Kampionii

Wykonał:

1. OBLICZENIA STATYCZNO-WYTRZYMAŁOŚCIOWE DLA PŁYTY

• Siatka stropu: załączony rysunek.

• Schemat statyczny: belka dwunastoprzęsłowa, którą w obliczeniach można uprościć do belki pięcioprzęsłowej o szerokości 1 m, obciążonej równomiernie

obciążeniem użytkowym i obliczeniowym.

• Wstępne założenia:

Przyjmuję:

- klasa ekspozycji betonu XC3

- klasa betonu B25 f_cd = 13,3 MPa, f_ck=20MPa, f_ctm=2,2MPa

- klasa stali A-I f_yd = 210 MPa, f_yk=240MPa, f_tk=320MPa

- grubość płyty h=0,1m

- szerokość przekroju poprzecznego b=1,0 m

- zbrojenie ϕ = 8 mm

• Rozpiętość efektywna l_eff :

Zakładam: - grubość płyty h = 0,1 m

- szerokość oparcia płyty na wieńcu t = 0,25 m

- szerokość oparcia płyty na żebrach b = 0,2 m

Rozpiętość efektywną wyliczam ze wzoru:

l_eff = l_n + a_n1 + a_n2

Schemat statyczny płyty składa się 12 przęseł i można go uprościć do belki 5 przęsłowej.( 2 przęsła skrajne i przyskrajne, 1 przęsło środkowe)

l_n1 = 1,9 - 0,2/2 = 1,8 m

l_n2 = 2,1 - 2*0,1 = 1,9 m

a_n1 = min( 0,05 ; 12,5 ) = 0,05 m

a_n2 = min( 0,05 ; 0,1 ) = 0,05 m

l_eff1 = l_n1 + a_n1 + a_n2 = 1,8 + 0,05 + 0,05

l_eff1 = 1,9 m

l_eff2 = l_n2 + 2*a_n2 = 1,9 + 0,05 + 0,05

l_eff2 = 2,0 m

Schemat do korzystania z Tablic Winklera:

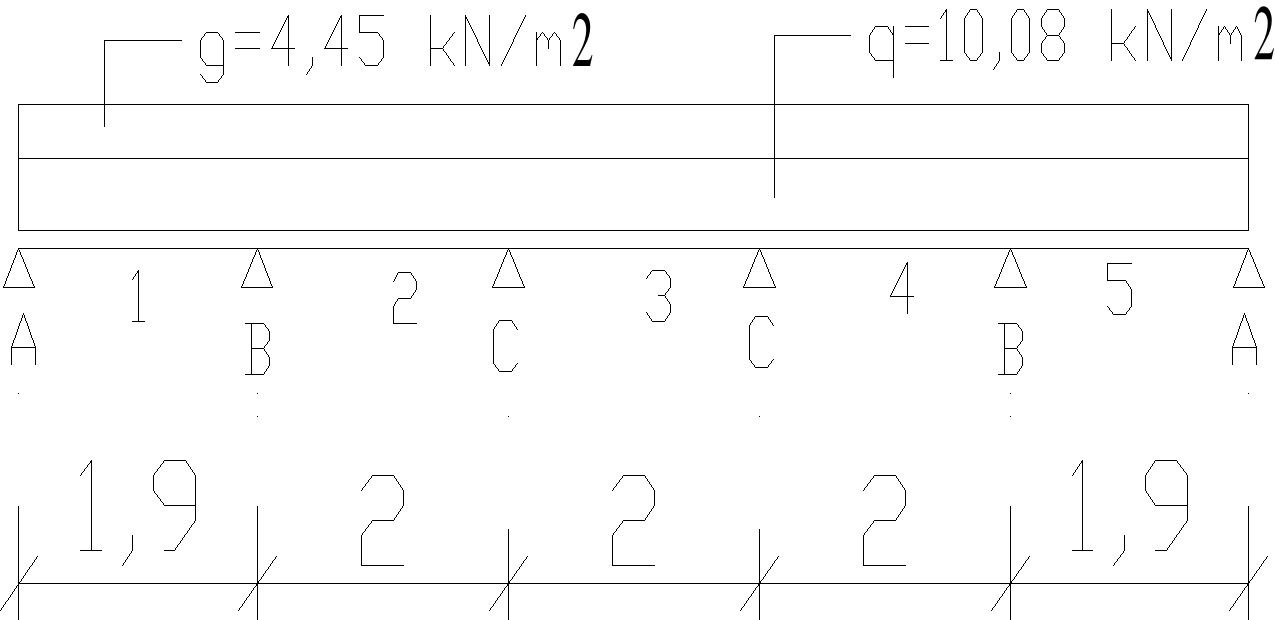
Rodzaj obciążenia	Obciążenie charakt. [kN/m^3]	Współczynnik obciążenia γf	Obciążenie obliczeniowe [kN/m^3]
Obciążenia stałe: - płytki granitogres na zaprawie cementowej 0,44 - gładź cementowa 4 cm 0,04*21,0 - styropian 4 cm 0,04*0,45 - izolacja 0,02 - płyta żelbetowa 10 cm 0,1*25,0 0,1*25,0	0,44 0,84 0,018 0,02 2.5	1,3 1,3 1,2 1,2 1,1	0,57 1,09 0,02 0,02 2,75
Razem	g = 3,82	-	g = 4,45
Obciążenie użytkowe	qk = 8,4	1,2	q = 10,08
Ogółem	gk+qk = 12,22	-	g+q = 14,53

• Zestawienie obciążeń przypadających na płytę:

Schemat statyczny płyty:

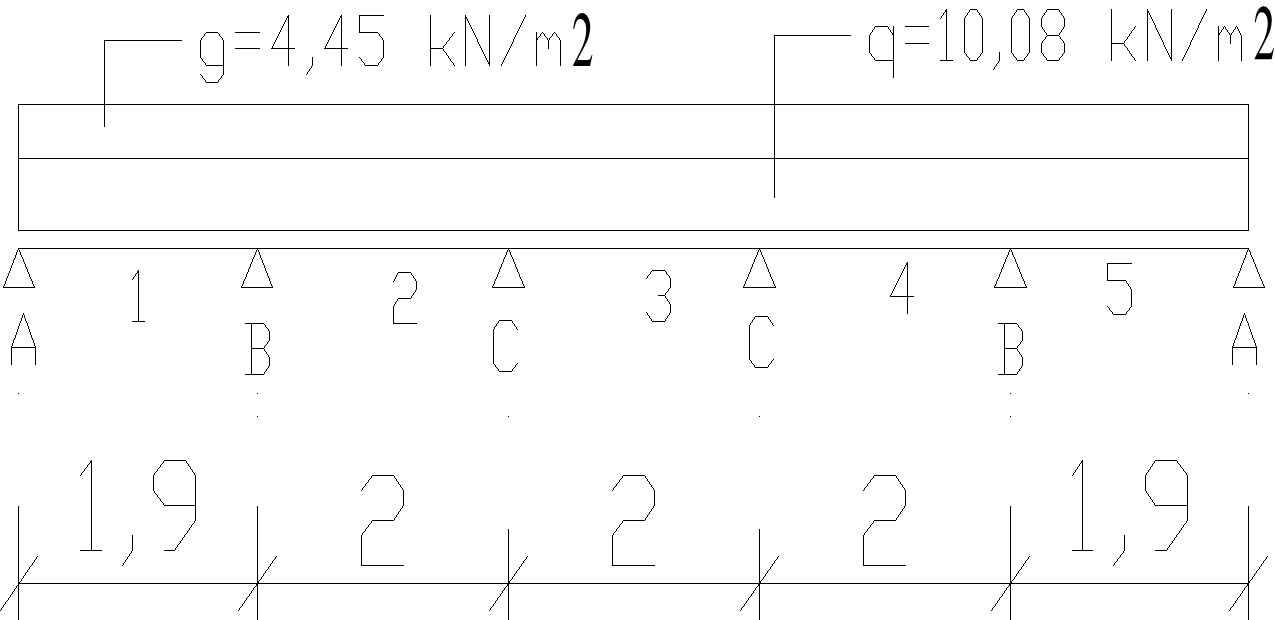
• Obliczenie wartości momentów zginających przy użyciu tablic Winklera:

Mi=a1*g*l²+a2*q*l² [kNm]

Qi=a3*g*l+a4*p*l [kN]

g - obciążenie stałe równomiernie rozłożone [kN/m]

q - obciążenie użytkowe równomiernie rozłożone [kN/m]

a1; a2; a3; a4 - współczynniki Winklera

l - długość przęsła [m]

M₁ = (0,0781*4,45 + 0,100*10,08)*1,9² = 4,89 kNm

M₂ = (0,0331*4,45 + 0,0787*10,08)*2,0² = 3,76 kNm

M₃ = (0,0462*4,45 + 0,0855*10,08)*2,0² = 4,23 kNm

M_B = -(0,105*4,45 + 0,119*10,08)*[0,5*(2,0+1,9)]² = -6,34 kNm

M_C = -(0,079*4,45 + 0,111*10,08)*(2,0)² = -5,88 kNm

M_1min = (0,0781*4,45 - 0,0263*10,08)*1,9² = 0,3 kNm

M_2min = (0,0331*4,45 - 0,0461*10,08)*2,0² = -1,27 kNm

M_3min = (0,0462*4,45 - 0,0395*10,08)*2,0² = -0,77 kNm

M_Bmin,odp = -(0,105*4,45 + 0,053*10,08)*[0,5*(2,0+1,9)]² = -3,81 kNm

M_Cmin,odp = -(0,079*4,45 + 0,040*10,08)*(2,0)² = -3,02 kNm

V_BLmax = -(0,605*4,45 + 0,62*10,08)*2,0= -17,88 kN

V_BPmax =(0,525*4,45 + 0,598*10,08)*2,0= 16,73 kN

V_CLmax = -(0,474*4,45 + 0,576*10,08)*2,0= -15,83 kN

V_CPmax = (0,500*4,45 + 0,591*10,08)*2,0= 16,36 kN

Wykres momentów zginających w płycie:

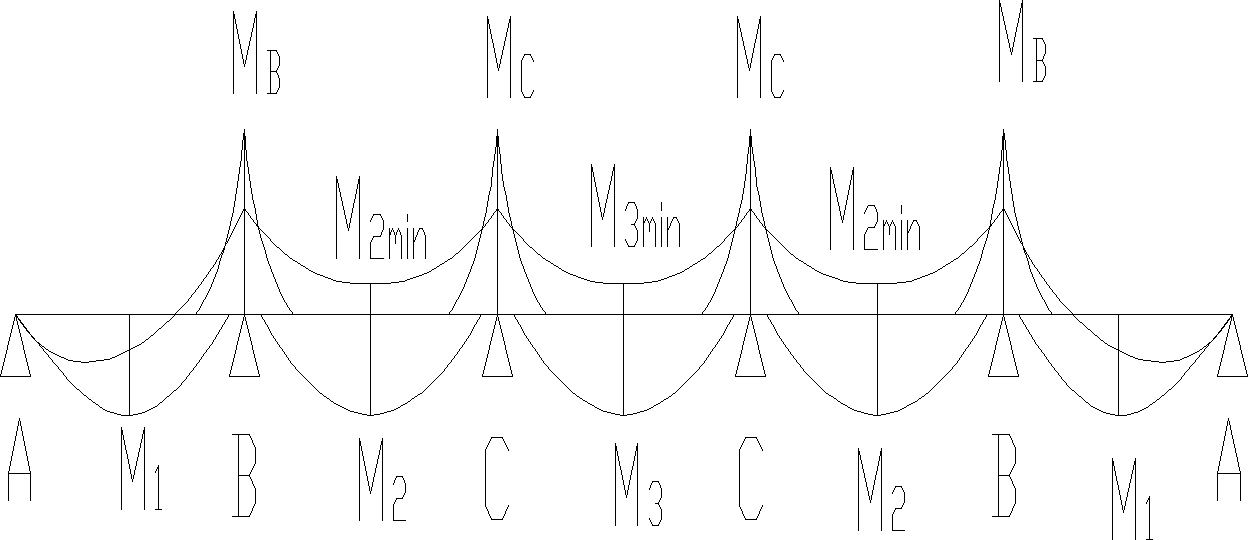
• Grubość otulenia prętów c_nom:

c_nom = c_min + Δc ,

Z tablicy 21. c_min = 20 mm

Przyjmuję Δc = 5 mm

c_nom = 25 mm

a₁= c_nom + 0,5 ϕ

d= h-a₁

d = 100 - 25 - 4 = 71 mm

d = 71 mm

• Wymiarowanie elementów. Obliczenie pola zbrojenia:

- przęsło skrajne:

M_sd = 4,89 kNm

Ponieważ:
przekrój może być pojedynczo zbrojony.

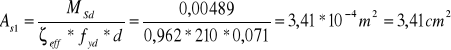
Przyjęto 8 ϕ 8 mm, wtedy A_s1 = 4,02 cm²

- przęsło przyskrajne:

M_sd = 3,76 kNm

Ponieważ:
przekrój może być pojedynczo zbrojony.

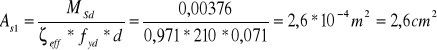
Przyjęto 10 ϕ 6 mm, wtedy A_s1 = 2,83 cm²

- przęsło środkowe:

Ponieważ moment w tym przęśle różni się nieznacznie od momentu w przęśle skrajnym zatem przyjmuje zbrojenie identyczne tzn. 8 ϕ 8 mm .

- Sprawdzenie warunku minimalnego pola przekroju zbrojenia podłużnego:

Przyjęty przekróje zbrojenia są większy od minimalnych określonych na podstawie powyższych warunków.

Ostatecznie stopień zbrojenia w przęsłach płyty wynosi:

- rozstaw prętów w przekroju:

Według normy rozstaw prętów zbrojenia w przekrojach krytycznych płyt dla

wysokości przekroju h = 0,1 m powinien być nie większy niż 0,12 m.

W naszym przypadku na 1 m szerokości przypada 8 i 10 prętów ϕ 8 i ϕ 6 mm.

Przy maksymalnym rozstawie prętów 12 cm min. liczba prętów w przekroju:

s = 1,0 / 0,12 = 8,(3) ≈ 8 prętów

- podpory przedskrajne (B) i pośrednie (C)

Obliczenia zostaną przeprowadzone w dwóch przekrojach:

1. w osi podpory,

2. w krawędzi podpory,

Momenty na podporach wynoszą:

M_B = 6,34 kNm

M_C = 5,88 kNm

Obliczenia dla podpory B:

Zbrojenie w osi podpory:

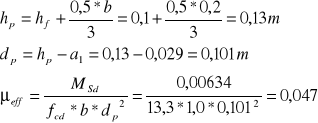
Ponieważ:
przekrój może być pojedynczo zbrojony.

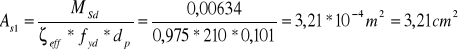
Zbrojenie na krawędzi podpory:

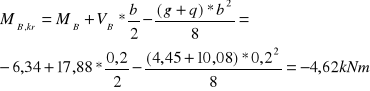
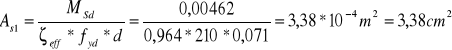
Przyjęto 8 ϕ 8 mm, wtedy A_s1 = 4,02 cm²

Obliczenia dla podpory C:

Zbrojenie w osi podpory:

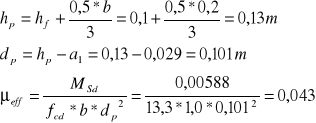
Ponieważ:
przekrój może być pojedynczo zbrojony.

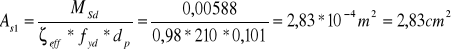
Zbrojenie na krawędzi podpory:

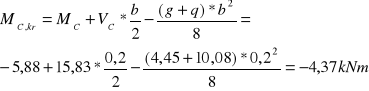
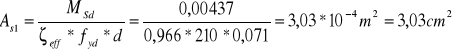
Przyjęto 8 ϕ 8 mm, wtedy A_s1 = 4,02 cm²

- podpora skrajna (A)

Na podporze zastosowane zostanie zbrojenie górne na długości

0,2*l_s = 0,2*1,8 = 0,36 m

Przekrój zbrojenia powinien wynieść co najmniej 25% zbrojenia

przęsłowego: przyjmuję 4 ϕ 6 mm co 250 mm

- długość zakotwienia prętów na podporach:

Minimalna długość zakotwienia:

l_min = 5ϕ = 40cm

Przyjmuję: l_bd = 10 cm

- zbrojenie rozdzielcze:

Przyjmuję: 4 ϕ 4,5 mm co 25 cm, pole przekroju 0,64 cm²

- zbrojenie na minimalne momenty przęsłowe:

Nośność płyty niezbrojonej określa wzór:

Moment zginający ujemny, występujący w przęśle:

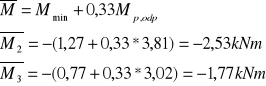
Nośność płyty niezbrojonej określa wzór:

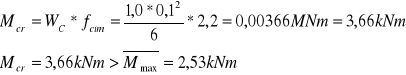
Moment rysujący jest większy od momentów minimalnych w przęsłach.

Oznacza to, że płyta nie wymaga dodatkowego zbrojenia górą.

• Sprawdzenie stanu granicznego zarysowania:

Moment charakterystyczny od obciążeń długotrwałych w przęśle pośrednim wynosi:

Naprężenie w zbrojeniu (dla
przyjęto
) obliczam z wzoru:

Dla uzyskanego naprężenia wartość ϕ_max = 32 mm.

Ponieważ zastosowano zbrojenie ϕ = 8 mm (ϕ < ϕ_max),zatem graniczna wartość rys

w_lim = 0,3 mm nie zostanie przekroczona

• Sprawdzenie stanu granicznego ugięć:

Obliczenia zostaną przeprowadzone metodą uproszczoną:

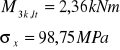
Wartość maksymalna: (l_eff/d)_min = 33,8 , należy skorygować współczynnikami:

- δ₁ =1,0 (rozpiętość płyty nie przekracza 6,0 m)

- δ₂ = 250/σ_s = 2,53

Uzyskany wynik oznacza, iż nie ma potrzeby sprawdzania ugięć metodą

dokładną.

2. OBLICZENIA STATYCZNO-WYTRZYMAŁOŚCIOWE DLA ŻEBRA:

• Schemat statyczny: belka trójprzęsłowa o przekroju teowym, obciążona równo-miernie ciężarem własnym i obciążeniem użytkowym.

• Grubość otulenia prętów zbrojenia c_nom:

c_nom = c_min + Δc ,

Z tablicy 21. c_min = 20 mm

Przyjmuję: - Δc = 5 mm , ϕ 8mm (dla strzemion), ϕ 20 mm (dla prętów)

- c_nom = 20 + 5 = 25 mm,

- c = c_nom + ϕ = 33 mm,

- a₁ = c + ϕ_p/2 = 33 + 10 = 43 mm,

Przyjmuję a₁ = 45 mm,

c_nom = 33 mm, a₁ = 45mm

• Rozpiętość efektywna l_eff :

Zakładam: - szerokość podpory skrajnej na murze t = 0,25 m

- szerokość oparcia płyty na żebra na podciągu b = 0,35 m

Rozpiętość efektywną wyliczam ze wzoru:

l_eff = l_n + a_n1 + a_n2

Schemat statyczny płyty składa się 3przęseł( 2 skrajne, 1 środkowe )

l_n1 = 6,0 - 0,35/2 = 5,825 m

l_n2 = 6,1 - 0,35 = 5,75 m

a_n1 = min( 0,125 ; 0,175 ) = 0,125 m

a_n2 = 0,175 m

l_eff1 = l_n1 + a_n1 + a_n2 = 5,825 + 0,125 + 0,175

l_eff1 = 6,125 m

l_eff2 = l_n2 + 2*a_n2 = 5,75 + 2*0,175

l_eff2 = 6,1 m

Schemat do korzystania z Tablic Winklera:

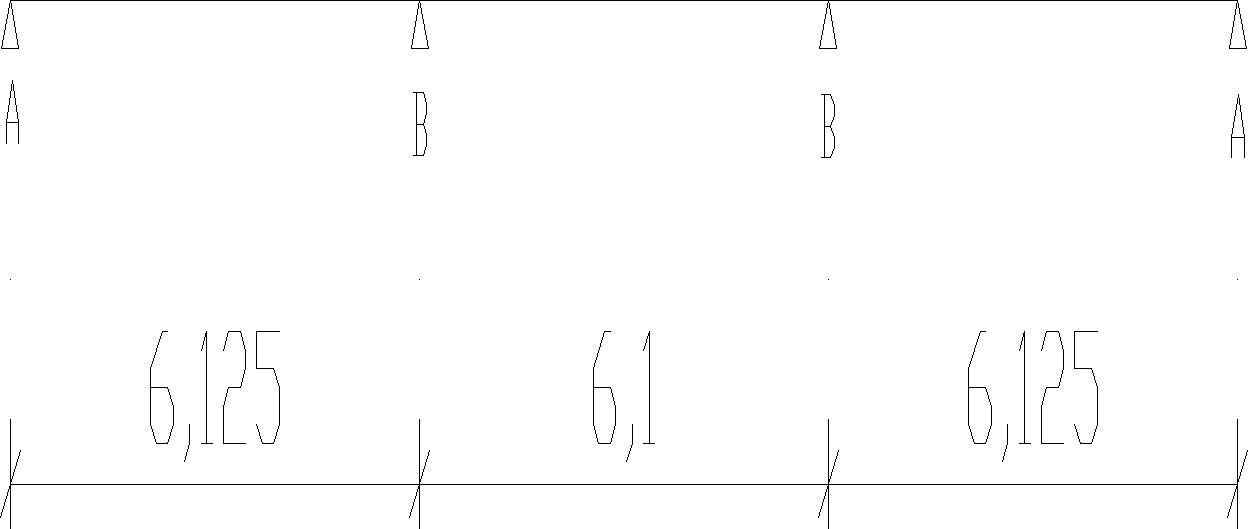
• Zestawienie obciążeń przypadających na żebro (na podstawie zebrania obciążeń dla płyty):

Razem	g = 3,82	-	g = 4,45
Obciążenie użytkowe	qk = 8,4	1,2	q = 10,08
Ogółem	gk+qk = 12,22	-	g+q = 14,53

Obciążenia stałe

- 3,82*2,1 = 8,02 kN/m

- 4,45*2,1 = 9,45 kN/m

Ciężar własny żebra (na podstawie wstępnie przyjętych wymiarów):

- 25,0*0,20*(0,50-0,10) = 2,0 kN/m

- 2,0*1,1 = 2,2 kN/m

Razem:

- g_k = 8,02 + 2,0 = 10,02 kN/m

- g = 9,45 + 2,2 = 11,65 kN/m

Obciążenia użytkowe:

- q_k = 8,4*2,1 = 17,64 kN/m

- q = 17,64*1,2 = 21,17 kN/m

Obciążenie całkowite:

- g_k +q_k = 10,02+17,64 = 27,66 kN/m

- g + q = 11,65+21,17 = 32,82 kN/m

Schemat statyczny żebra:




• Wymiary przekroju poprzecznego:

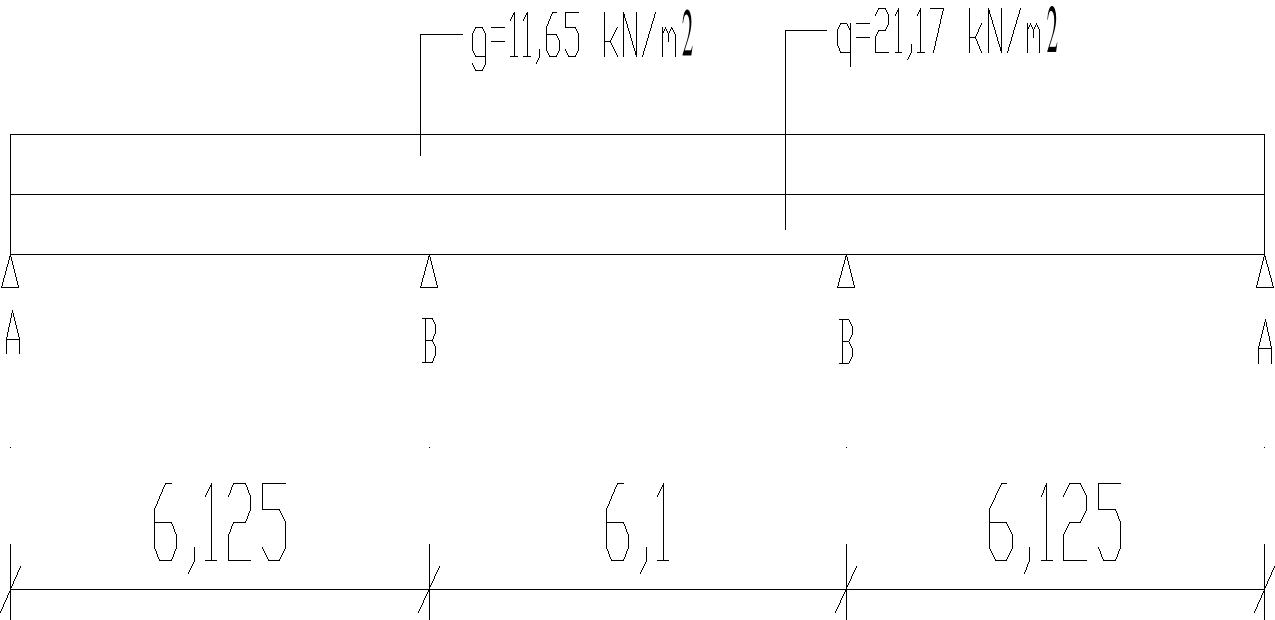
Wymiary przekroju poprzecznego zostaną dobrane tak by były spełnione wymagania stanów granicznych nośności i ugięć

- wymiary przekroju ze względu na stan graniczny nośności:

Dane: - obciążenie obliczeniowe g+q = 32,82 kN/m

- rozpiętość efektywna przęsła żebra l_eff = 6,125 m

- moment przęsłowy obliczony szacunkowo jak dla belki swobodnie

podpartej z wzoru:




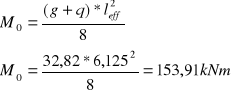
Ponieważ belka ma 3 przęsła moment M₀ należy odpowiednio zmniejszyć:




Do obliczeń przyjmuję:

- klasa betonu B25 f_cd = 13,3 MPa,

- klasa stali A-III f_yd = 350 MPa,

- szerokość żebra b = 0,2m

- zbrojenie ϕ 20 mm

- stopień zbrojenia


Obliczenie wysokości żebra:




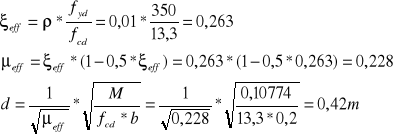
Wysokość użyteczną d należy powiększyć o grubość otuliny c = 33mm, i poło- wę średnicy zbrojenia głównego. W przypadku ułożenia zbrojenia (przyjmuję

ϕ20) w jednym rzędzie:

a₁ = 33 +0,5*20 = 43mm

Wysokość belki ustala się stopniując wymiary co 5 cm, przyjmuję:

h = 0,5 m ; b = 0,2 m

- wymiary przekroju poprzecznego ze względu na stan graniczny ugięć:

Obliczenia przeprowadzane są nadal dla przęsła skrajnego o l_eff = 6,125 m.

Należy sprawdzić wartość stosunku: l_eff/d, przy której nie będzie przekroczone dopuszczalne ugięcie sprawdzanego elementu konstrukcji.

Dla stopnia zbrojenia
, i betonu klasy B25 maksymalna wartość z tabe- li z normy:







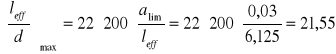
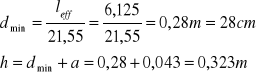
Ze względu na stan graniczny ugięć otrzymano mniejszą wysokość belki aniże- li dla stanu granicznego nośności. Ostatecznie przyjmuję wymiary przekroju uzyskane uprzednio.

• Obliczenie momentów zginających i sił poprzecznych:

Obliczenia zostaną przeprowadzone z wykorzystaniem tablic Winklera

Mi=a1*g*l²+a2*q*l² [kNm]

Qi=a3*g*l+a4*p*l [kN]

g - obciążenie stałe równomiernie rozłożone [kN/m]

q - obciążenie użytkowe równomiernie rozłożone [kN/m]

a1; a2; a3; a4 - współczynniki Winklera

l - długość przęsła [m]

M₁ = (0,08*11,65 + 0,101*21,17)*6,125² = 115,18 kNm

M₂ = (0,025*11,65 + 0,075*21,17)*6,1² = 69,92 kNm

M_B = -(0,1*11,65 + 0,117*21,17)*[0,5*(6,1+6,125)]² = -136,07 kNm

M_2min = (0,025*11,65 - 0,05*21,17)*6,1² = -28,55 kNm

M_Bmin,odp = -(0,1*11,65 + 0,051*21,17)* [0,5*(6,1+6,125)]² =-83,87 kNm

V_Amax = (0,4*11,65 + 0,45*21,17)*6,125 = 86,89 kN

V_BLmax = -(0,6*11,65 + 0,617*21,17)*6,125= -122,82 kN

V_BPmax =(0,5*11,65 + 0,583*21,17)*6,1= 110,82 kN

Wykres momentów zginających w płycie:




• Geometria przekroju poprzecznego żebra:

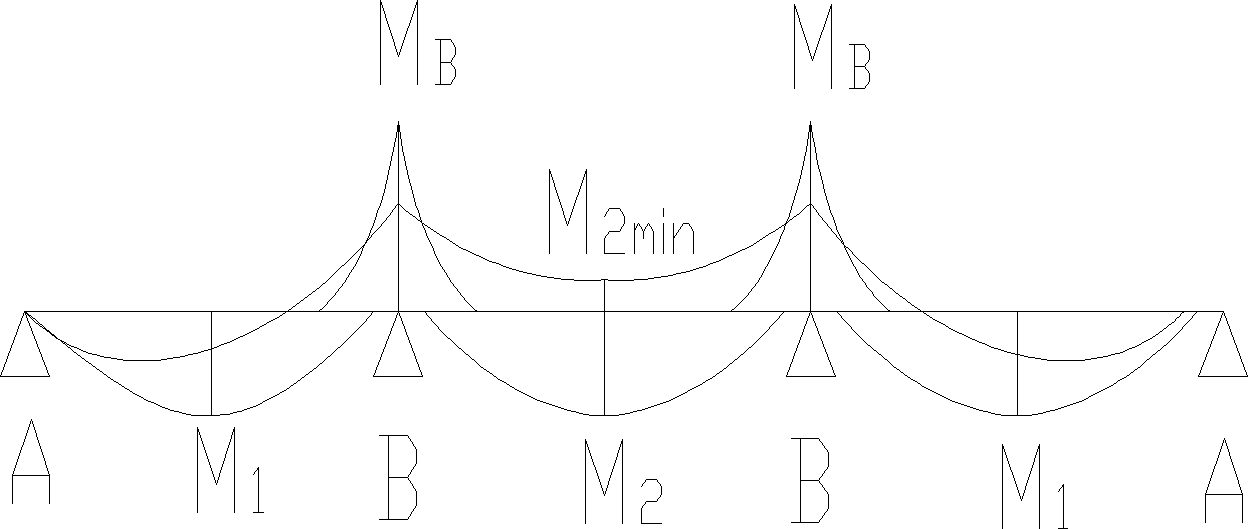
Żebro wraz z płytą tworzą przekrój teowy.

l_eff = 6,125 / 6,1 m

h = 0,5 m ; b_w = 0,2 m ; t = 0,25 m ; h_f = 0,1 ; b₁ = b₂ = 0,95 m ;

Wartość l₀ :

- dla przęseł skrajnych: l₀ = 0,85*l₁ = 0,85*6,125 = 5,21 m

- dla przęsła środkowego: l₀ = 0,7*l₂ = 0,7*6,1 = 4,27 m

Szerokość płyty współpracującej z żebrem dla wszystkich stanów granicznych:

b_eff = b_w + 0,2*l₀ ≤ b_w + b₁ + b₂

- Przęsło skrajne:

b_eff = 0,2 + 0,2*5,21 = 1,242 m ≤ 0,2 + 0,95*2 = 2,1 m

b_eff = 1,24 m

b_eff1 = b_eff2 = 0,52 m

W stanie granicznym nośności:

b_eff = b_w + b_eff1 + b_eff2

b_eff1 = b_eff2 = 6*h_f = 0,6 m

b_eff = 0,2 + 2*0,6 = 1,40 m

Do obliczeń stanu granicznego nośności przyjmuję mniejszą wartość szeroko- ści płyty współpracującej z belką czyli b_eff = 1,24 m

- Przęsło środkowe:

b_eff = 0,2 + 0,2*4,27 = 1,054 m ≤ 0,2 + 0,95*2 = 2,1 m

b_eff = 1,054 m

b_eff1 = b_eff2 = 0,427 = 0,43 m

W stanie granicznym nośności:

b_eff = b_w + b_eff1 + b_eff2

b_eff1 = b_eff2 = 6*h_f = 0,6 m

b_eff = 0,2 + 2*0,6 = 1,40 m

Do obliczeń stanu granicznego nośności przyjmuję mniejszą wartość szeroko- ści płyty współpracującej z belką czyli b_eff = 1,05 m

• Wymiarowanie żebra: I Stan graniczny nośności:

1) Obliczenie pola przekroju zbrojenia podłużnego z uwagi na zginanie:

A. Zbrojenie w przęśle :

Przęsło skrajne:

M₁ = 115,18 kNm

h = 0,5 m; b = 0,2 m ; b_eff = 1,24 m ; a₁ = 0,043 m,

d = h - a₁ = 0,457 m

Sprawdzam położenie osi obojętnej w celu ustalenia czy przekrój jest pozo- rnie czy rzeczywiście teowy. Zakładam ze x_eff = h_f i następnie wyliczam no- śność przy tym założeniu.




Zatem przekrój jest pozornie teowy.







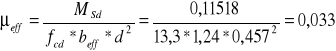
Zatem przekrój może być pojedynczo zbrojony.







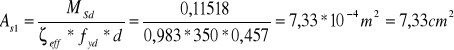
Przyjęto 3 ϕ 20 mm, wtedy A_s1 = 9,42 cm²

Przęsło środkowe:

M₂ = 69,92 kNm

h = 0,5 m; b = 0,2 m ; b_eff = 1,05 m ; a₁ = 0,043 m,

d = h - a₁ = 0,457 m

Sprawdzam położenie osi obojętnej w celu ustalenia czy przekrój jest pozo- rnie czy rzeczywiście teowy. Zakładam ze x_eff = h_f i następnie wyliczam no- śność przy tym założeniu.




Zatem przekrój jest pozornie teowy.







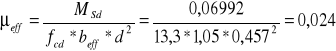
Zatem przekrój może być pojedynczo zbrojony.







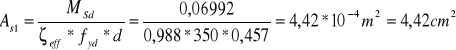
Przyjęto 2 ϕ 20 mm, wtedy A_s1 = 6,28 cm²

Ostatecznie stopień zbrojenia w przęsłach płyty wynosi:







Sprawdzenie warunku minimalnego pola przekroju zbrojenia podłużnego:







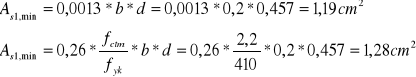
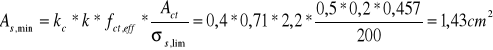
Przyjęte przekroje zbrojenia są większe od minimalnego określonego na podstawie powyższych warunków.

B. Zbrojenie na podporach B.

Zbrojenie obliczamy w osi i na krawędzi podpory:




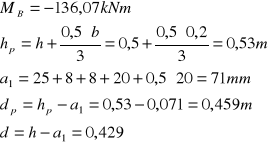
Wartość a₁ wyliczono uwzględniając: otulinę 25 mm, pręty zbrojenia płyty ϕ = 8 mm, strzemię belki ϕ = 8 mm, średnicę zbrojenia na podpo- rze ϕ = 20 mm, oraz połowę odległości między dwoma rzędami zbroje- nia ( przyjmuję s = 20 mm ).

Zbrojenie w osi podpory:














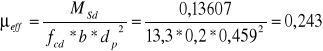
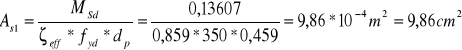
Zbrojenie na krawędzi podpory:
















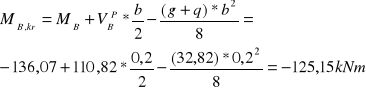
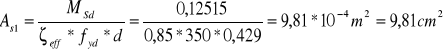
Przyjęto 4 ϕ 20 mm, wtedy A_s1 = 12,56 cm²

Stopień zbrojenia na podporze B:




C. Zbrojenie na minimalny moment przęsłowy:

Nośność płyty niezbrojonej określa wzór:




Moment zginający ujemny, występujący w przęśle:







Moment rysujący jest mniejszy od momentu minimalnego w przęśle

środkowym. Oznacza to, że płyta wymaga dodatkowego zbrojenia górą.







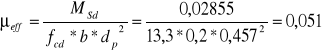
Zatem przekrój może być pojedynczo zbrojony.







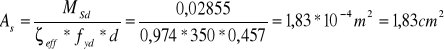
Przyjęto 2 ϕ 12 mm, wtedy A_s1 = 2,26 cm²

Przyjęte pole przekroju zbrojenia jest większe od minimalnego obliczo- nego w punkcie A.

2) Obliczanie pola przekroju zbrojenia z uwagi na ścinanie:

A. Podpora skrajna

V_Sd = V_A = 86,89 kN

V_Sd,_kr = V_A - (g+q)*0,5t = 86,89 - ( 32,82 ) *0,5*0,25 = 82,79 kN

Należy sprawdzic czy obliczanie nośności na ścinanie jest konieczne. W tym celu określamy obliczeniową nośność na ścinanie V_Rd1 w elemencie bez zbrojenia poprzecznego z wzoru:




k = 1,6 - d = 1,6 - 0,457 = 1,143

Do podpory doprowadzono 3ϕ 20, A_sL = 9,42 cm²








ponieważ belka nie jest obciążona siłą ściskającą





Zatem konieczne jest obliczenie dodatkowego zbrojenia poprzecznego na odcinku drugiego rodzaju.

Nośność ściskanych krzyżulców betonowych określam z wzoru:


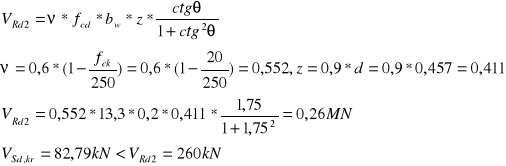
Zatem nośność krzyżulców betonowych jest wystarczająca.

Długość odcinka drugiego rodzaju określam z wzoru:




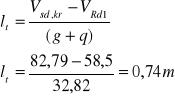
Rozstaw strzemion obliczam przyjmując, że:

- zbrojenie na ścinanie składa się wyłącznie ze strzemion pionowych,

- strzemiona są dwuramienne ϕ 8 ze stali A-I,

- strzemiona przenoszą całą siłę poprzeczną V_Sdkr tak więc V_Sdkr = V_Rd3,

- cotθ = 1,75 ,




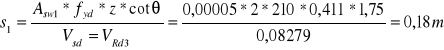
Przyjmuję: - l_t = 0,75 m,

- s₁ = 0,18 m dla strzemion dwuramiennych,

Minimalny stopień zbrojenia strzemionami:




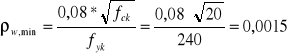
Stopień zbrojenia strzemionami:




Zaprojektowane zbrojenie strzemionami prostopadłymi do osi belki za-pewnia nośność na ścinanie na odcinku drugiego rodzaju.

Sprawdzenie, czy zbrojenie podłużne doprowadzone do skrajnej podpo-ry przeniesie siłę rozciągającą ΔF_td obliczoną z uwzględnieniem siły po

przecznej:




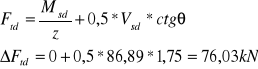
Do przeniesienia siły ΔF_td wystarczy zbrojenie podłużne o przekroju:




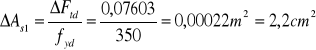
W przypadku podpory skrajnej (gdy M_sd = 0) jest to minimalny przekrój

zbrojenia, które należy doprowadzić i odpowiednio zakotwić. Do skra-jnej podpory doprowadzono 3 pręty ϕ 20 , których pole przekroju zape-wnia przeniesienie siły rozciągającej ΔF_td , ponieważ:

A_s1 = 9,42 cm² > ΔA_s1 = 2,2 cm²

Obliczenie długości zakotwienia prętów podłużnych 3 ϕ 20 doprowadzo-nych do skrajnej podpory:




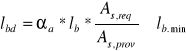
α_a - 1,0 (dla prętów prostych),

f_bd - 2,3 MPa,

-





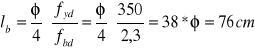
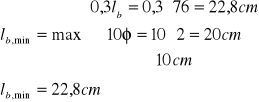
A_s,prov - pole przekroju zbrojenia zastosowanego 3 ϕ 20 = 9,42 cm²,

Wymaganą powierzchnię zbrojenia A_s,req należy przyjąć z uwagi na:

- minimalny przekrój zbrojenia podłużnego w elementach zginanych, w rozważanym przypadku A_s,min = 1,28 cm²

- przekrój potrzebny do przeniesienia siły ΔF_td czyli ΔA_s1 = 2,2 cm²

Przyjmuję A_s,req = 2,2 cm²




Szerokość podpory skrajnej t = 25 cm, przyjmuję l_bd = 25 cm, tak więc ze względu na ścinanie pręty doprowadzone do skrajnej podpory będą do-

statecznie zakotwione.

Długość zakotwienia prętów podłużnych 3 ϕ 20 mm na podporze pośre- dniej określono jak dla elementu, w którym doprowadzono do podpory co najmniej 2/3 prętów z przęsła oraz l_eff/h > 12 (6,125/0,5=12,25>12).

Zbrojenie podłużne żebra musi być przedłużone poza krawędź podpory pośredniej o odcinek nie krótszy niż 10 ϕ tj. 20 cm.

Ponieważ l_b,min=22,8 cm , przyjęto długość zakotwienia równą 23 cm.

Sprawdzenie ścinania między środnikiem a półkami w przekroju z półką

ściskaną. Podłużna siła ścinająca przypadająca na jednostkę długości je- dnostronnego połączenia półki ze środnikiem:




Półka żebra jest ściskana między punktami zerowych momentów na dłu- gości, którą można oszacować jako:

l₀ = 0,85*l_eff = 0,85*6,125 = 5,21 m

Rozpatrzono odcinek Δx, który jest połową odległości między przekro- jami M = 0 oraz M = |M_max|

Δx =0,25 * l₀ = 0,25 * 5,21 = 1,3 m

Siła poprzeczna w odległości 1,3 m od podpory A:




Średnia wartość siły poprzecznej na odcinku Δx:







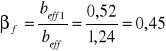
z = 0,9*d = 0,9*0,457 = 0,411








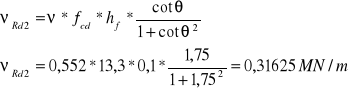
Zbrojenie płyty A_sf = 0,00005 m² (ϕ8 mm), rozstaw s_f = 0,12 m







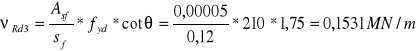
Zatem ścinanie między środnikiem a półkami nie wystąpi.

B. Podpora środkowa.

V_Sd: V_BL = 122,82 kN

V_BP = 110,82 kN

V_Sd,_krL = V_BL - (g+q)*0,5t = 122,82 - ( 32,82 ) *0,5*0,35 = 117,08 kN

V_Sd,_krP = V_BP - (g+q)*0,5t = 110,82 - ( 32,82 ) *0,5*0,35 = 105,08kN




k = 1,6 - d = 1,6 - 0,429 = 1,171

Do podpory doprowadzono:

- 4ϕ 20, A_sL = 12,56 cm²




- 4ϕ 20, A_sP = 12,56 cm²








ponieważ belka nie jest obciążona siłą ściskającą






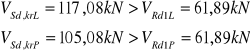
Zatem konieczne jest obliczenie dodatkowego zbrojenia poprzecznego na odcinku drugiego rodzaju.

Nośność ściskanych krzyżulców betonowych określam z wzoru:




(Oznaczenia podobnie jak dla podpory A.)




Zatem nośność krzyżulców betonowych jest wystarczająca.

Długość odcinka drugiego rodzaju:




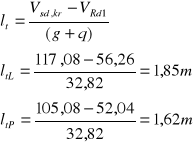
Rozstaw strzemion obliczam, przyjmując założenia obliczeniowe jak na podporze skrajnej. Wtedy:







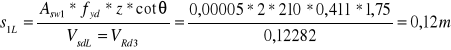
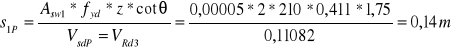
Przyjmuję: - l_tL = 1,85 m,

- s_1L = 0,12 m dla strzemion dwuramiennych,

- l_tP = 1,62 m

- s_1P = 0,14 m dla strzemion dwuramiennych,

Minimalny stopień zbrojenia strzemionami
=0,0015 zatem stopień zbrojenia strzemionami wynosi:




Zaprojektowane zbrojenie strzemionami prostopadłymi do osi belki za-pewnia nośność na ścinanie na odcinku drugiego rodzaju.

Maksymalny rozstaw strzemion s_max :

s_max ≤ 0,75*d = 0,75*0,429 = 0,323 m

s_max ≤ 400 mm

W projektowanej belce przyjęto na odcinkach pierwszego rodzaju rozstaw strzemion …. cm.

Sprawdzenie, nośności zbrojenia podłużnego ze względu na przyrost siły rozciągającej ΔF_td , spowodowanej ukośnym zarysowaniem wy-konano w odległości d od krawędzi podpory.

Siła poprzeczna w odległości d od krawędzi podpory







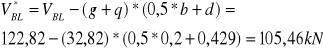
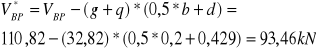
Moment w odległości d od krawędzi podpory:








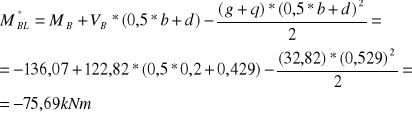
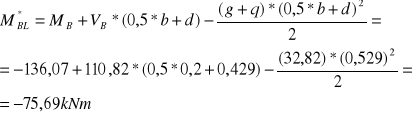
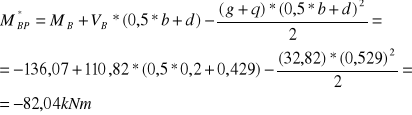
Sumaryczna siła rozciągająca w odległości d od krawędzi podpory:


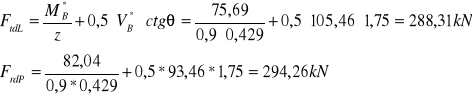
PPrzekrój zbrojenia potrzebny do przeniesienia siły F_td:




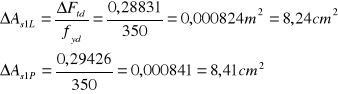
Nad podporą doprowadzono 3 oraz 2 pręty ϕ 20 , których pole przekroju zapewnia przeniesienie siły rozciągającej ΔF_td , ponieważ:

A_s1 = 12,56 cm² ;A_s2 = 12,56 cm² > ΔA_s1L = 8,24cm² ^ ΔA_s1P = 8,41 cm²

Ponieważ półka znajduje się w strefie rozciąganej , nie jest konieczne sprawdze- nie ścinania między środnikiem a półkami.

Jedynym zbrojeniem półki równoległym do osi żebra jest zbrojenie rozdzielcze, którego przekrój jest stosunkowo mały. W związku z tym stosunek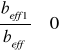


czyli
.

---