CEL ĆWICZENIA
Ćwiczenie wykonane przez nas miało na celu wyznaczenie transmitancji zastępczych zbudowanych obiektów regulacji, zawierających elementy automatyki połączone szeregowo, równolegle i ze sprzężeniem zwrotnym oraz wykreślenie ich charakterystyk czasowych.
PRZEBIEG ĆWICZENIA
Postacie równań układu dla układu liniowego:
![]()
- równanie stanu
![]()
- równanie wyjścia
Współczynniki A, B, C, D w powyższych równaniach są macierzami, których elementami
są liczby zależne od struktury i parametrów opisywanego układu.
BADANIE PODSTAWOWYCH CZŁONÓW DYNAMICZNYCH.
Wyznaczanie charakterystyk obiektów regulacji ma na celu eksperymentalne ustalenie właściwości obiektów w przypadkach, w których równania wyrażające te właściwości
nie są dostatecznie znane. Rozróżnia się pomiary właściwości statycznych i właściwości dynamicznych. Pomiary właściwości statycznych są stosunkowo proste i muszą być wykonane w całym zakresie zmian wielkości wejściowych i wyjściowych. Pomiary dynamiczne z reguły sprowadzamy do pomiarów w liniowym zakresie działania badanego obiektu, operując małymi odchyleniami od wybranego punktu pracy.
Istnieją trzy zasadnicze metody wyznaczania właściwości dynamicznych:
- wyznaczanie przebiegu przejściowego przy zdeterminowanym sygnale wymuszającym
(wyznaczanie charakterystyk czasowych),
- wyznaczanie charakterystyk częstotliwościowych (wyznaczanie przebiegów ustalonych przy
wymuszeniach sinusoidalnych),
- badanie właściwości przebiegów czasowych przypadkowych (stochastycznych).
W pewnym uproszczeniu można przyjąć, że najpewniejsze i najdokładniejsze wyniki daje wyznaczenie charakterystyk częstotliwościowych. Miejsce pośrednie zajmuje badanie przebiegu przejściowego przy określonym sygnale wymuszającym. Na ogól najmniej dokładne oraz wymagające dosyć żmudnego opracowania wyników są badania przebiegów stochastycznych.
Proporcjonalny
Ogólna postać równań elementu:
y=kx
y-wielkość wyjściowa;
x-wielkość wejściowa;
k-współczynnik proporcjonalności (współczynnik wzmocnienia).
Transmitancja G(s)=y(s)/x(s)=k
Równanie charakterystyki statycznej y=kx lub yo=kxo+C
C-stała określająca przesunięcie charakterystyki w stosunku do układu współrzędnych.
Wymuszenie skokowe x(t)=1(t)xst będzie y(t)=1(t)kxst
![]()
![]()
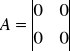
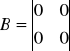
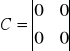
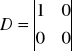
Całkujący
Ogólna postać równania różniczkowego dy/dt=kx lub po scałkowaniu , przy zerowych
warunkach początkowych y=koƒt x dt
transmitancja G(s)=y(s) / x(s) =k/s współcz. k k=dy/dt /x
wymuszenie skokowe x(t)=1(t)xst wyznaczamy
y(s)=k/s ∗x(s)=k/s2 ∗ xst
y(t)=α-1[y(s)]=kxstt
Gdy wejście i wyjście są sygnałami jednoimiennymi , współczynnik k ma wymiar odwrotności czasu . Tdy/dt=x której odpowiada transmitancja G(s)=y(s)/x(s)=1/Ts
T-stała czasowa akcji całkującej (stała całkująca)
{G(s)=k/s(1+Ts)}
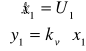
![]()
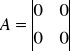
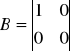
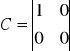
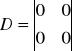
Inercyjny
Ogólna postać równania różniczkowego elementu inercyjnego I rzędu : T dy/dt + y=kx
transmitancja G(s)=y(s)/x(s) = k/ Ts+1 k- współczynnik proporcjonalności ;
T- stała czasowa
równanie charakterystyki statycznej y=kx
wymuszenie skokowe x(t)=1(t)xst zgodnie z tablic otrzymujemy : x(s)=1/s∗xst
y(s)=k/s(Ts+1) xst=k/T xst ∗ 1/s(s+1/T)
y(t)=α-1[y(s)]=k/T xstT(1-e-t/T)
y(t)=kxst(1-e-t/T)
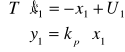
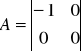
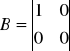
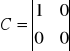
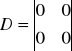
Różniczkujący rzeczywisty
Idealny element różniczkujący
równanie idealnego elementu różniczkującego y=k dx/dt
transmitancja G(s)=y(s)/x(s)=ks
współczynnik k definiuje się k= y/(dx/dt) w stanie ustalonym y=0 (yo=const) dla wszystkich x
odpowiedzią na wymuszenie skokowe jest funkcja Diraca pomnożona przez k oraz przez amplitudę skoku xst y(s)=ksx(s)=kxst na podstawie tabeli y(t)=α-1[y(s)]=kxstδ(t)
a zatem y(t)={ 0 dla t<0 ; ∞ dla t=0 ; 0 dla t>0
w przypadku gdy wejście i wyjście są sygnałami jednoimiennymi równanie zapisuje się w postaci y=T dx/dt transmitancja : G(s)=y(s)/x(s)=Ts T-stała różniczkowania
Rzeczywiste elementy różniczkujące
ogólna postać równania rzeczywistego elementu różniczkującego : T dy/dt +y =k dx/dt
transmitancja G(s)=y(s)/x(s)=Ts/Ts+1
odpowiedź na wymuszenie skokowe z transmitancji y(s)=ks/Ts+1 ;
x(s)=kxst /Ts+1=k/T xst1 /s+1/T ; y(t)=α-1[y(s)]=k/T xst e-t/T
Proporcjonalno całkujący
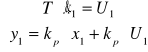
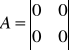
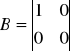
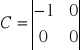
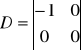
Dwuinercyjny
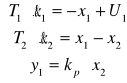
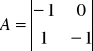
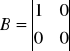
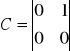
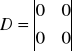
Oscylacyjny
Ogólna postać równania różniczkowego oscylacyjnego
T12 d2y/dt2 + T2 dy/dt + y = kx , przy czym T22<4T12
transmitancja G(s)=y(s)/x(s)=k/ T12 s2 +T2 s+1
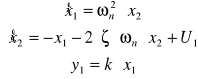
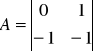
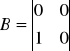
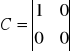
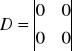
W badanych układach im większa była wartość wymuszenia, tym większe były odpowiedzi układów. Na podstawie otrzymanych wykresów odpowiedzi na skok jednostkowy można stwierdzić prawidłowość zamodelowania powyższych członów dynamicznych, gdyż zgadzają się z wykresami teoretycznymi. Na podstawie wykresów odpowiedzi można określić wpływ zmian wartości macierzy na modelowany układ.
BADANIE PROSTEGO UKŁADU REGULACJI, KTÓREGO SCHEMAT JEST PODANY NIŻEJ
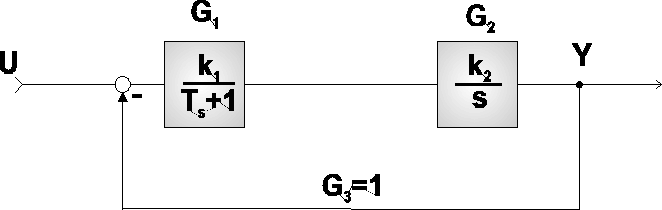
k1=k2=1 T=1
RÓWNANIE STANU TEGO UKŁADU
![]()
Transmitancja dwóch elementów połączonych szeregowo
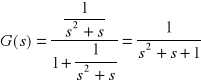
Transmitancja wypadkowa.
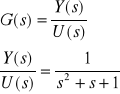
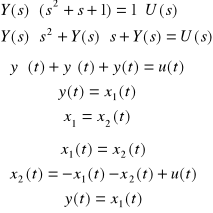
Z powyższego układu równań wypisujemy macierze:
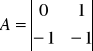
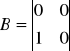
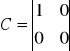
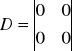
Odpowiedź na wartość wymuszenia skokowego danego modelu układu przedstawia wykres. Z wykresu wynika, że badany układ regulacji jest członem oscylującym.
Następnym krokiem jest sprawdzenie, czy układ jest sterowalny.
Układ jest sterowalny - jeżeli istnieje ograniczony przedziałami ciągłymi, wektor sterowania U(t) przeprowadzający ten układ z dowolnego stanu początkowego x(to) do dowolnego stanu końcowego x(tk) w skończonym czasie tk-to≥0.
![]()
- równanie stanu (liniowy stacjonarny ciągły)
![]()
- równanie wyjścia
Układ jest sterowalny, gdy możemy w każdej chwili sterować całym układem, a nie tylko poszczególnymi czasami.
Układ jest sterowalny wtedy i tylko wtedy, gdy rząd macierzy Q jest równy wymiarowi n wektora stanu, czyli gdy istnieje zbiór n wektorów liniowo niezależnych.
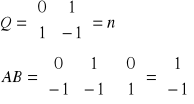
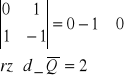
Nasz układ jest sterowalny.
Sprawdzamy, czy układ jest obserwowalny.
Układ jest obserwowalny - jeżeli przy dowolnym wektorze sterowania U(t) istnieje skończona chwila tk , po której można wyznaczyć stan układu x(to) w dowolne chwili początkowej to na podstawie znajomości wektora wyjściowego Y(t) i wektora sterowania U(t) w przedziale od to do tk.
Układ jest obserwowalny gdy możemy określić stan początkowy na podstawie obserwacji przebiegu sygnałów wyjściowych i sterujących.
Warunkiem koniecznym i dostatecznym obserwowalności jest, aby podany rząd macierzy był równy n
![]()
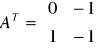
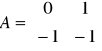
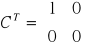
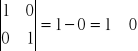
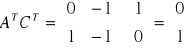
Układ jest obserwowalny.
Sprawdzenie stabilności układu.
Z analizy matematycznej wynika, że warunki stabilności układu są odniesione do równania różniczkowego układu zamkniętego -KRYTERIUM HURWITZA
Równanie różniczkowe układu ma postać :
a0s2+a1s+a2=0 , a2,a1,a0=1
Aby układ był spełniony muszą być spełnione następujące dwa warunki :
1. Wszystkie współczynniki ai równania charakterystycznego winny mieć ten sam znak ≥0.
2. Warunkiem koniecznym i wystarczającym aby układ był stabilny jest dodatni znak każdego
z ciągu podwyznaczników.
Wyznacznik główny ma postać:
a1 a0 0 1 1 0
Δ2 = 0 a2 a1 = 0 1 1 Δ2=1
0 0 0 0 0 0
Układ jest stabilny.
WNIOSKI
Układ dynamiczny, to dowolny układ fizyczny, rozpatrywany z punktu widzenia jego zachowania się w czasie. Otrzymane w trakcie ćwiczenia przebiegi z badanych układów dostarczają nam informację o stanie układu. Znając transmitancję układu można wyznaczyć odpowiedź Y(t) układu, przy dowolnym wymuszeniu u(t). Związki między wymuszeniami, a stanem układu nazywamy równaniami stanu. Do prostych układów możemy zaliczyć każdy układ dynamiczny posiadający jeden sygnał wejściowy i jeden sygnał wyjściowy, dający opis liniowy równaniem co najwyżej drugiego rzędu. Tak np. człon proporcjonalny można opisać równaniami y(t)=k⋅u(t) ;G(s)=k. Wykresem jest linia równoległa do osi rzędnych, odległość od osi zależy od wielkości wymuszenia, co jest zgodne z teorią.
1
6
Wyszukiwarka
Podobne podstrony:
Cwiczenie 2 - Regulatory dwustawne moje, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Autom
miszczu dynamiczne, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Automaty lab, Automaty, Ko
Sprawozdanie z cwiczenia nr 2moje, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Automaty la
Z2, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Automaty lab, Automaty, Zestawy
Moja ściąga 2. kolos, Szkoła, Semestr 4, Podstawy automatyki
Z9, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Automaty lab, Automaty, Zestawy
ZESTAW 1, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Automaty lab, Automaty, Zestawy
Przekazniki, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, automaty
156, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Automaty lab, Automaty, Kolos, Kolos
Sciaga234, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Automaty lab, Automaty, Kolos, Kolo
konop, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Automaty lab, Automaty, Kolos, Kolos
Przekazniki1, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, automaty
ZESTAW 6, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Automaty lab, Automaty, Zestawy
WNIOSKI UZUPEŁNIENIE, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Automaty lab, Automaty,
Z6, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Automaty lab, Automaty, Zestawy
automaty PID, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, automaty
więcej podobnych podstron