1. W oparciu o zasadę zachowania pędu i energii omów zderzenia sprężyste i niesprężyste.Energia to wielkość fizyczna charakteryzująca stan ciała (układu ciał) pod względem jego zdolności do wykonywania pracy (ruchu ciała). zależnie od różnych rodzajów procesów fizycznych mówimy o różnych formach energii: wewnętrznej mechanicznej elektromagnetycznej jądrowej chemicznej zasadniczo rozróżnia się energię: E_k kinetyczną - związaną z ruchem ciała U potencjalną - związaną z siłami działającymi na ciało i jego położeniem.Prawo zachowania energii mechanicznej

Jeżeli wszystkie siły działające na cząstkę są zachowawcze, to całkowita energia cząstki w każdym jej położeniu jest wielkością stałą, zwaną całkowitą energią mechaniczną siła niezachowawcza np. siła tarcia, ciepło, promieniowanie energia układu izolowanego może przekształcać się z jednej postaci w inną, jednak energia całkowita w jej różnorodnych formach nie może być ani stworzona z niczego, ani też unicestwiona

pęd cząstki o masie bezwładnej m i prędkości jest wektoremcałkowity pęd izolowanego i zamkniętego układu cząstek pozostaje stały
(jeśli na układ cząstek nie działają siły zewnętrzne lub ich wypadkowa jest równa zeru, to całkowity pęd układu nie ulga zmianie) pęd początkowy jest równy pędowi końcowemu

jeśli wypadkowa sił zewnętrznych jest wzdłuż pewnej osi równa zeru, to składowa pędu w tym kierunku nie ulega zmianie Zderzenie sprężyste Zderzeniem nazywamy krótkotrwały proces, w którym jakieś ciała zbliżają się do siebie, a następnie w wyniku wzajemnego oddziaływania ich ruch ulega zmianie. Zasada zachowania pędu
Zasada zachowania energii

Zasada zachowania energii

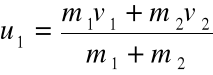
b. . Układ inercjalny (inaczej inercyjny) - układ odniesienia, względem którego każde ciało, niepodlegające zewnętrznemu oddziaływaniu z innymi ciałami, porusza się bez przyspieszenia (tzn. ruchem jednostajnym prostoliniowym lub pozostaje w spoczynku). Istnienie takiego układu jest postulowane przez pierwszą zasadę dynamiki Newtona. Zgodnie z zasadą względności Galileusza wszystkie inercjalne układy odniesienia są równouprawnione i wszystkie prawa mechaniki i fizyki są w nich identyczne. Inercjalny układ odniesienia można również zdefiniować jako taki układ, w którym nie pojawiają się pozorne siły bezwładności.c. Nieinercjalny układ odniesienia - układ odniesienia poruszający się ruchem niejednostajnym względem jakiegokolwiek inercjalnego układu odniesienia. Transformacja równań ruchu z układu inercjalnego do układu nieinercjalnego powoduje, że w równaniu ruchu zapisanym w układzie nieinercjalnym pojawiają się dodatkowe wyrazy, których wartość zależy od ruchu układu nieinercjalnego względem inercjalnego. Wyrazy te mają wymiar siły i dlatego mówimy, że w takim układzie występują pozorne siły. Przykładem takich sił jest siła bezwładności i siła Coriolisa. Przyspieszenie (siła) nie są niezmiennicze przy przejściu z jednego układu do drugiego


W układzie nieinercjalnym do sił rzeczywiście działających trzeba dodać siły bezwładności - zmodyfikowane drugie prawo Newtona d. d. Omów doświadczenie Michelsona - Morley'a jego wynik i wpływ na „pojawienie się” szczególnej teorii względności Eksperyment miał na celu, poprzez porównanie prędkości światła w różnych kierunkach względem Ziemi, wykazanie ruchu Ziemi względem hipotetycznego eteru. Albert Michelson uznał, że do określenia prędkości wiatru eteru nie potrzeba wyznaczać prędkości światła, wystarczy porównać prędkość światła w różnych kierunkach. Skonstruował przyrząd zwany interferometrem Michelsona. W interferometrze wiązka światła zostaje podzielona półprzezroczystą płytką na dwie prostopadłe wiązki, które po odbiciu od zwierciadeł i po powtórnym przejściu przez płytkę trafiają do teleskopu, w którym widać jasne i ciemne prążki jako wynik interferencji obu wiązek. Obraz interferencji zależy od różnicy czasu przebiegu obu wiązek między płytką a zwierciadłami, bo w pozostałej części drogi światła obie wiązki biegną tą samą drogą. Gdyby czas przebycia światła między płytką a zwierciadłem 1 zmienił się o inną wartość niż czas dla drugiej drogi, to układ prążków interferencyjnych przesunąłby się. W ten sposób można wyznaczyć nawet niewielkie różnice w prędkości rozchodzenia się światła. Gdyby istniał wiatr eteru, wystarczyłoby obrócić interferometr, a układ prążków powinien przesuwać się. Michelson oszacował że dokładność pomiaru urządzenia jest 4 razy większa od przesunięcia prążków, jakie powinien uzyskać dla prędkości ruchu Ziemi wokół Słońca. Ku swojemu zaskoczeniu nie wykrył ruchu prążków. Michelson postanowił powtórzyć doświadczenie, dokonał tego razem z E. Morleyem. W doświadczeniu tym zwiększono dziesięciokrotnie długość drogi światła, zwiększając dokładność pomiaru. By zapobiec nawet najmniejszym drganiom zwierciadeł, układ interferometru pływał w korytach wypełnionych rtęcią. Pomimo takiej precyzji i przeprowadzenia wielu doświadczeń w wielu kierunkach, przez rok nie zauważono zmian w układzie prążków interferencyjnych. Jedną z hipotez przedstawił Hendrik Antoon Lorentz. Zaproponował, że ruch ciał względem eteru skraca długość ciała o czynnik . Było to początkiem przekształcenia znanego obecnie jako transformacja Lorentza. Ostatecznym wyjaśnieniem tego efektu i upadku koncepcji eteru było ogłoszenie przez A. Einsteina w 1905 roku założeń szczególnej teorii względności z jej głównym postulatem głoszącym, że prędkość światła w próżni jest jednakowa we wszystkich inercjalnych układach odniesienia. f. Drgania swobodne: Niech na sprężynie będzie zaczepiona masa m, Gdy wychylamy ciało o masie m z położenia równowagi x = 0 o x to zgodnie z definicją siły sprężystej na układ działa siła Fs=-kx; siła spręż Fs jest prop do wych x i przeciwnie do niego skierowana. Zgodnie z II zasadą dynamiki Newtona: można napisać -kx= m*d²x/dt² oznaczając: ώ₀²=k/m można napisać: d²x/dt²=-ώ₀²x =>równ ruchu drgań swob p mat. rozw: x(t)=A₀cos(ώ₀t+φ₀) Punkt mat wykonujący drgania harm nosi nazwę oscylatora harm nietłumionego. E_p=kx²; E_k=mv²/2; E=E_p+E_k=1/2*mώ₀² A₀² g. Omów drgania harmoniczne tłumione. Jeżeli drgania ciała odbywają się w ośrodku materialnym (np. w gazie, cieczy), to wskutek występowania siły oporu ośrodka, którą będziemy nazywać siłą tłumiącą, drgania będą zanikać. Niezależnie od natury ośrodka siła tłumiąca
jest proporcjonalna do prędkości
ciała drgającego (jeżeli prędkość ta jest niewielka). Zatem
. Współczynnik proporcjonalności
nazywa się współczynnikiem oporu ośrodka. Znak minus w powyższym wzorze uwzględnia fakt, że siła jest zawsze skierowana przeciwnie do kierunku ruchu (kierunku prędkości).Uwzględniając działanie siły możemy dla drgaż tłumionych, zgodnie z II zasadą dynamiki napisać
, czyli
albo
.Pamiętając, że
(częstość kołowa drgań własnych) oraz oznaczając formalnie
to z ww. wzoru otrzymujemy
. Równanie to nosi nazwę równania ruchu drgań harmonicznych tłumionych. Jest to równanie równanie różniczkowe rzędu drugiego, jednorodne. Rozwiązaniem tego równania jest funkcja
, gdzie:
(współczynnik tłumienia;
(pulsacja drgań tłumionych).Porównując wzór dla drgań swobodnych ze wzorem dla drgań tłumionych widzimy, że wskutek działania siły tłumiącej: 1.amplituda drgań tłumionych maleje z upływem czasu według zależności
; 2. Pulsacja drgań tłumionych jest mniejsza niż dla drgań swobodnych
. Wielkością charakteryzującą drgania tłumione jest tzw. Logarytmiczny dekrement tłumienia. h. Omów drgania wymuszone. Jeżeli chcemy , aby opory ośrodka nie tłumiły drgań, to na drgający punkt materialny należy działa odpowiednio zmienną w czasie siłą. W przypadku drgań harmonicznych siła ta ma postać:
Siłę tę nazywamy wymuszającą. W przypadku drgań wymuszających mamy
Czyli
albo

co można zapisać (1)
gdzie
(1)- równanie nosi nazwę równania ruchu drgań wymuszonych. Rozwiązaniem tego równania jest funkcja
gdzie
,
. i. Istota ruchu falowego Większość wiadomości, jakie mamy o świecie zewnętrznym, dociera do naszej świadomości poprzez organa zmysłowe słuchu i wzroku za pośrednictwem fal. Informacje te dochodzą do obserwatora z pewnym opóźnieniem wynikającym ze skończonej prędkości światła i dźwięku. Rozpatrzymy teraz sytuację, w której drgająca cząstka jest połączona poprzez siły sprężyste z innymi cząstkami (rys.6.10). Wskutek działania między cząstkami sił sprężystych drgania będą przenosiły się od jednej cząstki do drugiej. Z podobną sytuacją spotykamy się w ciałach stałych i gazach. Jako przykład rozpatrzmy gaz. Jeśli w pewnym miejscu sprężymy gaz, np. na skutek ruchu tłoka, to w obszarze tym znajdzie się więcej cząstek. Spowoduje to wzrost ciśnienia gazu i pojawienie się siły skierowanej w kierunku mniejszego ciśnienia (gęstości). Na skutek tego, tam gdzie gaz był zgęszczony, teraz ulegnie rozrzedzeniu i odwrotnie. Jeśli tłok będzie wykonywał ruch drgający, to w gazie będą rozprzestrzeniały się kolejne zgęszczenia i rozrzedzenia ośrodka. Omówione tutaj drgania sprężyste rozchodzące się w gazach, cieczach i ciałach stałych nazywamy falami sprężystymi. Fale sprężyste nazywamy też często falami akustycznymi, rozumiejąc przez ten termin fale sprężyste propagujące się we wszystkich stanach skupienia materii, w pełnym zakresie częstości drgań, jaki może wystąpić w przyrodzie. Okazuje się, że proces przekazywania drgań z jednego punktu do drugiego jest zjawiskiem charakterystycznym nie tylko dla ośrodków sprężystych, ale również dla pola elektromagnetycznego. Drgania pola elektromagnetycznego wytwarzają falę elektromagnetyczną. W tym przypadku zmieniającymi się wielkościami są pola: elektryczne i magnetyczne. Charakterystyczną cechą takiego zaburzenia jest fakt, że może ono propagować się również w próżni. Na podstawie licznych obserwacji fizycznych możemy powiedzieć, że fale to nic innego jak rozchodzące się w przestrzeni zaburzenia stanu materii lub pola. Wspólną cechą wszystkich zjawisk falowych jest zdolność przenoszenia przez falę energii, przy czym w procesie tym występuje w sposób ciągły okresowa zamiana energii jednego rodzaju na drugi rodzaj. Np. w przypadku fal sprężystych mamy ciągłą zamianę energii kinetycznej cząstek materii na energię potencjalną, a w przypadku fal elektromagnetycznych energia pola elektrycznego przechodzi w energię pola magnetycznego i na odwrót. J.Interferencja fal Rozważmy dwie fale o równych częstotliwościach i amplitudach ale o fazach różniących się o ϕ. Równania tych fal są następujące y₁ = Asin(kx - ωt - ϕ) y₂ = Asin(kx - ωt) Znajdźmy teraz falę wypadkową (zasada superpozycji) jako sumę y = y₁ + y₂. Korzystając ze wzoru na sumę sinusów otrzymujemy y = 2Acos(ϕ/2)sin(kx - ωt - ϕ/2) ϕ/2)sin(kx - ωt - ϕ/2) co jest równaniem fali sinusoidalnej o amplitudzie 2Acos(ϕ/2). Dla ϕ = 0 fale spotykają się zgodnie w fazie (wzmacniają), a dla ϕ = 180 wygaszają. Interferencją fal nazywamy zjawisko nakładania się (superpozycji) dwóch lub więcej fal o tych samych długościach, a więc o tych samych pulsacjach. l. . Omów II zasadę termodynamiki (o czym nam mówi, cykl Carlota, sformułowania II zasady i ich omówienie, entropia) II zasada termodynamiki:a)nie można zbudować perpetum mobile drugiego rodzaju b)gdy dwa ciała o różnych temperaturach znajdą się w kontakcie termicznym wówczas ciepło będzie przepływało z cieplejszego do chłodniejszego d)żadna cykliczna maszyna cieplna pracująca pomiędzy temperaturami T₁ i T₂ nie może mieć sprawności większej (T₁-T₂)/T₁ c)w układzie zamkniętym entropia nie może maleć. ENTROPIA-jest miarą nieuporządkowania układu cząstek. Im większy jest stan nieporządku położeń i prędkości w układzie tym większe prawdopodobieństwo że układ będzie w tym stanie. CYKL CARNOTA-obieg termodynamiczny składa się z dwóch przemian izotermicznych i dwóch przemian adiabatycznych. Jest cyklem odwracalnym. Do realizacji cyklu potrzebne jest czynnik roboczy (wykonujący prace i można nad nim wykonać) np. gaz z tłokiem także dwa źródła ciepła pierwsze jako źródło (o temp. T₁)- górne źródło drugie jako chłodnica (o temp. T₂)-dolne źródło. Przebieg Cyklu-1.sprężenie izotermiczne-gaz styka się z chłodnicą ma temp. Chłodnicy i zostaje sprężony w temp.T₂ gaz oddaje ciepło do chłodnicy -2.sprężenie adiabatyczne-gaz nie wymienia ciepła z otoczeniem jest sprężany aż osiągnie temp. Źródła ciepła (T₁)-3.Rozprężanie izotermiczne gaz styka się ze źródłem ciepła ma jego temperaturę i zostaje rozprężony w temp. (T₁) gaz pobiera ciepło z otoczenia-4.rozprężenie adiabatyczne gaz nie wymienia ciepła jest rozprężany aż osiągnie temp. Chłodnicy (T₂)CYKL CARNOTA jest cyklem zamkniętym. Sprawność cyklu Carnota stosunek pracy wykonanej do ilości ciepła pobranego ze źródła ciepła.
=1-
Druga zasada termodynamiki Zwróćmy jeszcze raz uwagę na to, że w trakcie pracy (cyklu) silnika cieplnego część pobieranego ciepła była oddawana do zbiornika o niższej temperaturze i w konsekwencji ta ilość ciepła nie była zamieniana na pracę. Powstaje pytanie, czy można skonstruować urządzenie, które pobierałoby ciepło i w całości zamieniałoby je na pracę? Moglibyśmy wtedy wykorzystać ogromne (z naszego punktu widzenia nieskończone) ilości ciepła zgromadzone w oceanach, które byłyby stale uzupełniane poprzez promieniowanie słoneczne.Negatywna, niestety, odpowiedź na to pytanie jest zawarta w drugiej zasadzie termodynamiki. Poniżej podane zostały równoważne sformułowania tej zasady: Nie można zbudować perpetum mobile drugiego rodzaju.Gdy dwa ciała o różnych temperaturach znajdą się w kontakcie termicznym, wówczas ciepło będzie przepływało z cieplejszego do chłodniejszego. Żadna cykliczna maszyna cieplna pracująca pomiędzy temperaturami T₁ i T₂ nie może mieć sprawności większej niż (T₁ - T₂)/T₁. W układzie zamkniętym entropia nie może maleć. Rozpatrzmy następujący schemat (pokazany na rysunku poniżej),w którym super silnik o sprawności większej od silnika Carnota napędza ten silnik. Efektem końcowym jest przeniesienie dwóch jednostek ciepła z zimniejszego do cieplejszego zbiornika.m. omów prawo Archimedesa i równowaga ciał pływających m.Prawo Archimedesa - podstawowe prawo hydro- i aerostatyki określające siłę wyporu. Nazwa prawa wywodzi się od jego odkrywcy Archimedesa z Syrakuz Wersja współczesna: Na ciało zanurzone w płynie (cieczy, gazie lub plazmie) działa pionowa, skierowana ku górze siła wyporu. Wartość siły jest równa ciężarowi wypartego płynu. Siła ta jest wypadkową wszystkich sił parcia płynu na ciało. Stara wersja prawa: Ciało zanurzone w cieczy lub gazie traci pozornie na ciężarze tyle, ile waży ciecz lub gaz wyparty przez to ciało.Legenda głosi, że król Syrakuz zwrócił się do Archimedesa, aby ten zbadał, czy korona, którą wykonał dla Hierona II pewien syrakuzański złotnik, zawiera tylko złoto, czy jest to jedynie pozłacane srebro. Archimedes długo nad tym rozmyślał, aż wreszcie pewnego razu w czasie kąpieli w wannie poczuł jak w miarę zanurzania się w wodzie ciężar jego ciała się zmniejsza. Oszołomiony swoim odkryciem, wyskoczył z wanny i z okrzykiem Eureka! (Heureka, gr. ηὕρηκα - "znalazłem") nago wybiegł na ulicę i udał się do króla. Po otrzymaniu odpowiedniej wartości dla ciężaru właściwego korony Archimedes porównał ją z ciężarem właściwym czystego złota - okazało się, że korona nie była z niego wykonana. Pierwsza zasada termodynamiki To jest po prostu inna wersja zasady zachowania energii, w której mamy rozdzieloną energię ciała na część makroskopową i mikroskopową. Makroskopowa to energia ruchu masy (energia mechaniczna). Mikroskopowa to "ukryta" energia cząstek (energia wewnętrzna). Gdy dwa układy (ciała) o różnych temperaturach zetkniemy ze sobą to ciepło ၄Q przepływa z ciała cieplejszego do chłodniejszego. Zgodnie z zasadą zachowania energii, ciepło pobrane przez układ musi być równe wzrostowi energii wewnętrznej układu plus pracy wykonanej przez układ nad otoczeniem zewnętrznym czyli ၄Q = ၄U + ၄W  To jest sformułowanie I zasady termodynamiki. Zasada ta pracuje "w obie strony" tzn., gdy nad układem zostanie wykonana praca to układ może oddawać ciepło. To równanie bardzo często przybiera postać. dU = dQ - dW Ciepło właściwe Ciepło właściwe definiujemy jako dQ/dT na gram lub mol substancji (ciepło wagowe lub molowe).  Ciepło właściwe przy stałej objętości Ponieważ dV = 0 więc dU = dQ a stąd c_v = dQ/dT = dU/dT  Dla gazu jednoatomowego (dla jednego mola) U = (3/2)N_AVkT = (3/2)RT. Zatem c_v = (3/2)R  Dla cząsteczki dwuatomowej spodziewamy się więc  c_v = (5/2)R a dla wieloatomowejc_v = 3R Niedoskonałością modelu opartego na mechanice klasycznej jest to, że przewiduje ciepło właściwe niezależne od temperatury, a badania pokazują, że jest to prawdziwe tylko dla gazów jednoatomowych. Dla pozostałych c_v rośnie z temperaturą. Na rysunku poniżej przedstawiono c_V dla wodoru (H₂) w funkcji temperatury (w skali logarytmicznej). Zatem średnia energia wewnętrzna na cząsteczkę wynosi U = E_śr,kin,post + E_śr,kin,rot + E_śr,kin,drg + E_śr,pot,drg U = (3/2)kT + (2/2)kT + (1/2)kT + (1/2)kT = (7/2)kT Dla 1 mola U = (7/2)RT więc c_v = (7/2)R Ciepło właściwe przy stałym ciśnieniu Z I zasady termodynamiki mamy dQ = dU + pdV Ponieważ U zależy tylko od T więc mamy dU = c_vdT więc dQ = c_vdT + pdV  Dla gazu doskonałego (1 mola) dV = RdT/p, więc dQ = c_vdT + RdT skąd dQ/dT = c_v + R Ostatecznie więc c_p = c_v + R c_p = c_v + R Kinetyczno-molekularna teoria gazów — teoria, rozpatrująca budowę materii z punktu widzenia trzech podstawowych, w przybliżeniu słusznych założeń: wszystkie ciała składają się z cząstek, których rozmiary można pominąć: atomów, cząsteczek i jonów; cząstki znajdują się w nieprzerwanym, chaotycznym ruchu (cieplnym); cząstki oddziałują na siebie poprzez zderzenia sprężyste.
gdzie k jest stosunkiem stałej gazowej R do liczby Avogadro , а i - liczba stopni swobody cząsteczki. Podstawowe równanie Kinetyczno-molekularnej teorii gazów wiąże parametry makroskopowe (ciśnienie, objętość, temperatura) układu z mikroskopowymi (masa cząsteczki, prędkość średnia ich ruchu). Rozważmy sześcienne naczynie o krawędzi długości l i jedną cząstkę o masie m znajdującą się w nim. Oznaczmy prędkość cząstki przez v_x, wtedy przed zderzeniem ze ścianką naczynia pęd cząstki równy jest mv_x, zаś po - − mv_x, zatem ściance zostaje przekazany pęd p = 2mv_x. Czas, po którym cząstka zderzy się ponownie z tą samą ścianą wynosi
. Stąd:

zaś ciśnienie
.Odpowiednio,
и
. W ten sposób, dla dużej liczby cząstek prawdziwe jest następujące wyrażenie:
, analogicznie dla osi y i z.

Ponieważ
, tо
. Skąd
lub
. Niech
— średnia energia kinetyczna, а E_k — całkowita energia kinetyczna wszystkich cząsteczek, wtedy:
, czyli
, skąd
. k.

---