Rys. 3.5. Okno dialogowe Dodatki
Dr Maria Jadamus-Hacura
Opis arkusza wyników dodatku programowego „REGRESJA” programu Excel
Po wyborze postaci analitycznej funkcji trendu na podstawie oceny wzrokowej wykresów danych empirycznych, przechodzimy do drugiego etapu analizy szeregu czasowego tzn. do oszacowania parametrów strukturalnych (parametrów funkcji trendu) i stochastycznych (odchylenia standardowego składnika losowego) modelu oraz do oceny jakości otrzymanego modelu obliczając odpowiednie miary dokładności dopasowania funkcji trendu do danych empirycznych.
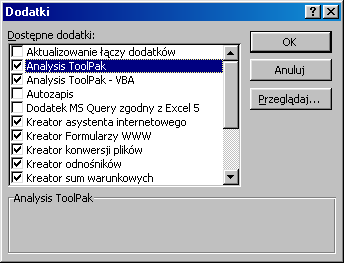
Do dokładnego oszacowania parametrów strukturalnych i stochastycznych modelu wykorzystamy narzędzie analizy danych programu Excel: Regresja. Jeżeli w opcji Narzędzia, w głównym menu arkusza, nie znajdujemy polecenia Analiza danych należy uaktywnić zbiór procedur programu Excel pod nazwą Dodatki. W tym celu z głównego menu wybieramy opcje: Narzędzia →Dodatki. W wyświetlonym wówczas oknie dialogowym uaktywniamy dodatki: Analysis ToolPak i Analysis ToolPak - VBA, co spowoduje zwiększenie liczby dostępnych funkcji obliczeniowych (rys. 1 .5)

Rys. 3.5. Okno dialogowe Dodatki
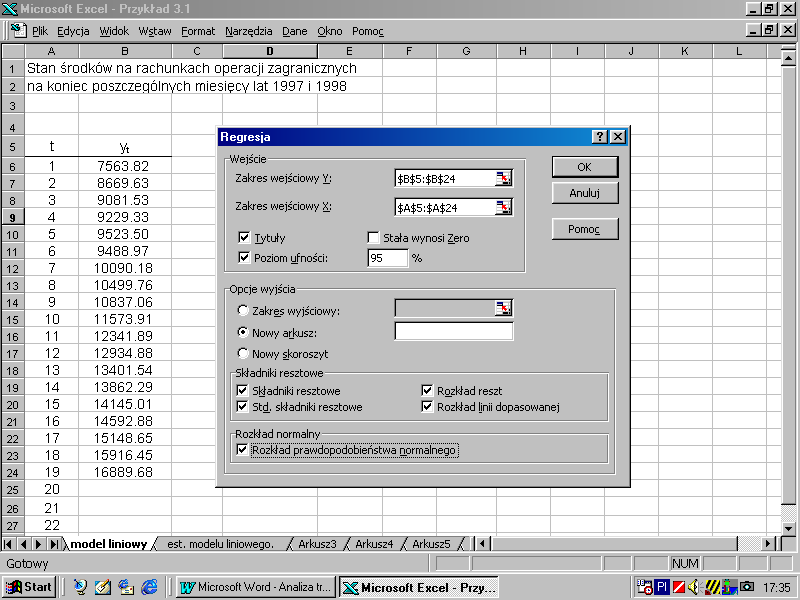
Po zainstalowaniu odpowiednich dodatków, w aktywnym oknie z wprowadzonymi danymi, z głównego menu wybieramy: Narzędzia→ Analiza danych→Regresja (rys. 3.6).
Opcja Regresja umożliwia oszacowanie parametrów modelu regresji liniowej postaci:
Yt = α0 + α1X1t +α2 X2t +.... +αk Xkt + εt (3.9)
gdzie: X1t, X2t, ... Xkt - zmienne objaśniające modelu
εt - składnik losowy modelu
αi - parametry strukturalne modelu
Zakres wejściowy Y obejmuje obserwacje zmiennej zależnej Y ( dla modeli trendu 1-3 jest to zmienna yt, natomiast dla modelu potęgowego i wykładniczego jest to zmienna ln(yt)). Natomiast Zakres wejściowy X obejmuje obserwacje zmiennych objaśniających występujących w modelu; przykładowo w modelu regresji wielorakiej (3.9) Zakres wejściowy X obejmie k kolumn obserwacji zmiennych X1t, X2t, ... Xkt, natomiast w przypadku trendu liniowego, którego analizę przeprowadzono w arkuszu roboczym na rys. 3.6 jest to zmienna t, której wartości w postaci kolejnych liczb naturalnych od 1-19 zaznaczono w komórkach A6:A19. Zaznaczenie opcji Stała wynosi Zero spowoduje, że wyraz wolny równania regresji wyniesie 0. Zaznaczenie pól wyboru Składniki resztowe spowoduje:
Składniki resztowe - obliczenie wartości reszt ![]()
;
Std. Składniki resztowe - obliczenie standaryzowanych wartości reszt
równych ilorazowi: ![]()
;
Rozkład reszt - otrzymanie wykresu wartości reszt względem każdej zmiennej objaśniającej, w przypadku trendu liniowego jest to wykres reszt w czasie;
Rozkład linii dopasowanej - otrzymanie wykresów wartości empirycznych i wartości teoretycznych, czyli wartości funkcji trendu;
Rozkład prawdopodobieństwa normalnego - otrzymanie wykresu krzywej częstości skumulowanych opartą na percentylach.
Rys. 3.6. Okno dialogowe Regresja
Po naciśnięciu przycisku OK w nowym arkuszu uzyskujemy podsumowanie regresji. Poszczególne tablice tego podsumowania przedstawiają tablice 3.1-3.3.
Tablica 3.1. Statystyki regresji
PODSUMOWANIE - WYJŚCIE |
||
Statystyki regresji |
uwagi |
|
Wielokrotność R |
0.9914 |
współczynnik korelacji wielorakiej |
R kwadrat |
0.9829 |
współczynnik determinacji |
Dopasowany R kwadrat |
0.9819 |
skorygowany współczynnik determinacji |
Błąd standardowy |
366.7 |
odchylenie standardowe reszt |
Obserwacje |
19 |
liczba obserwacji |
Współczynnik determinacji jest jedną z podstawowych miar dopasowania modelu regresji liniowej do danych empirycznych. Obliczamy go ze wzoru:
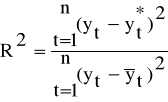
(3.10)
gdzie: n - liczebność próby (liczba okresów)
![]()
- wartość realizacji zmiennej prognozowanej w okresie t
![]()
- wartość teoretyczna wyznaczonej funkcji regresji dla t = 1,2,... ,n,
( w przypadku modeli tendencji rozwojowej są to wartości
wyznaczonej funkcji trendu)
Wartość współczynnika determinacji R2 zawiera się w przedziale <0,1> i informuje jaka część zaobserwowanej, całkowitej zmienności yt została wyjaśniona przez model trendu.
Współczynnik korelacji wielorakiej R jest równy dodatniemu pierwiastkowi z wartości współczynnika determinacji i mierzy siłę związku liniowego zmiennej objaśnianej Y ze zbiorem zmiennych objaśniających występujących w modelu.
Ponieważ wartość współczynnika determinacji R2 rośnie wraz z liczbą dodatkowych zmiennych objaśniających uwzględnionych w modelu, nie może on być używany do porównania stopnia dopasowania modeli o różnej liczbie zmiennych objaśniających. Do tego celu można wykorzystać skorygowany współczynnik determinacji ![]()
.
Dopasowany R kwadrat jest to skorygowany o liczbę zmiennych objaśniających w modelu współczynnik determinacji, który obliczamy ze wzoru:
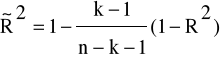
(3.11)
gdzie:
n- liczba obserwacji zmiennej objaśnianej
k- liczba zmiennych objaśniających występujących w modelu
Oba współczynniki determinacji stosujemy jedynie do modeli trendów liniowych i modeli liniowych względem parametrów . Współczynnik R2 nie może być używany jako miara dopasowania modelu wykładniczego i potęgowego w postaci (3.4) i (3.6) do danych empirycznych, gdyż współczynnik ten został policzony dla modelu liniowego, w którym zmienną zależną była zmienna zt = ln yt. Problemowi temu poświęcimy jeszcze uwagę przy omawianiu rozwiązań konkretnych przykładów zastosowania wspomnianych funkcji trendu.
Inną , bardzo ważną miarą dopasowania funkcji trendu do danych empirycznych jest odchylenie standardowe składnika resztowego, które obliczamy ze wzoru:
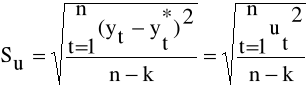
(3.12)
gdzie:
n - liczebność próby
k - liczba szacowanych parametrów
![]()
- wartość realizacji zmiennej prognozowanej w okresie t
![]()
- wartości teoretyczne, obliczone na podstawie oszacowanej funkcji
regresji
Wielkość odchylenia standardowego reszt interpretujemy jako przeciętne odchylenie zaobserwowanych wartości zmiennej yt od odpowiadających im wartości funkcji trendu.
Tablica 3.2. Analiza wariancji
ANALIZA WARIANCJI |
|||||
|
df |
SS |
MS |
F |
Istotność F |
Regresja |
1 |
131201713.6 |
131201713.6 |
975.691 |
1.86028E-16 |
Resztkowy |
17 |
2285997.385 |
134470.4344 |
|
|
Razem |
18 |
133487711 |
|
|
|
Oznaczenia:
df (degrees of freedom) - liczba stopni swobody
SS(Sum of Squares) - suma kwadratów
MS(Mean Squares) - średnie kwadraty (suma kwadratów podzielona przez liczbę stopni swobody)
Wiadomo, że jeżeli oszacujemy model regresji liniowej postaci (3.9) klasyczną metodą najmniejszych kwadratów, to zachodzi równość: suma kwadratów odchyleń zmiennej objaśnianej od jej wartości średniej (czyli zmienność zmiennej zależnej) jest sumą zmienności wyjaśnionej regresją i zmienności resztowej. Wartości te są zapisane w kolumnie trzeciej tablicy 3.2. Na ich podstawie została obliczona wartość statystyki F, która jest sprawdzianem następującej hipotezy:
H0 : R=0 (lub, αi =0, dla i=1,2,.. k)
H1: R > 0 (lub przynajmniej jedno αi≠0)
Zweryfikowanie tej hipotezy, o istotności współczynnika korelacji wielorakiej, pozwala na stwierdzenie, czy zbiór zmiennych objaśniających wpływa istotnie na zmienną y. Decyzję odnośnie przyjęcia bądź odrzucenia hipotezy H0 podejmujemy na podstawie wartości prawdopodobieństwa p = P(F>Fobl). Wartość Fobl znajduje się w kolumnie o tytule F, natomiast wartość prawdopodobieństwa p znajduje się w ostatniej kolumnie tablicy 3.2 i nosi nazwę Istotność F. Jeśli prawdopodobieństwo p jest nie większe od przyjętego poziomu istotności, to sprawdzaną hipotezę odrzucamy, czyli wartość współczynnika korelacji wielorakiej jest istotnie różna od zera.
Tablica 3.3 zawiera wyniki oszacowania parametrów strukturalnych modelu i pozwala na ocenę ich istotności.
Tablica 3.3. Wyniki oszacowania parametrów strukturalnych modelu
|
Współczynniki |
Błąd standardowy |
t Stat |
Wartość-p |
Dolne 95% |
Górne 95% |
Przecięcie |
7086.043 |
175.125 |
40.46 |
2.416E-18 |
6716.56 |
7455.52 |
t |
479.769 |
15.359 |
31.24 |
1.86E-16 |
447.36 |
512.17 |
Objaśnienia:
Bląd standardowy - średni błąd szacunku, miara precyzji oszacowania parametru strukturalnego modelu
T - Stat - iloraz ocen parametrów i średnich błędów szacunku
Wartość-p - wartość prawdopodobieństwa p = P(t>T-stat).
Dolne 95% - Górne 95% - końce przedziałów ufności wyznaczonych dla współczynników regresji dla współczynnika ufności 1-α = 0,95.
Istotnym punktem weryfikacji modelu jest sprawdzenie, czy uwzględnione w modelu zmienne objaśniające wpływają istotnie na kształtowanie się zmiennej objaśnianej. Sprawdzianem hipotezy zerowej
H0: αi =0,
wobec hipotezy alternatywnej H1: αi ≠0 jest statystyka t-Studenta o n-k-1 stopniach swobody równa ilorazowi oceny danego parametru i jego średniego błędu szacunku (są to wartości T - Stat podane w tablicy 3.2). Jeżeli wartość prawdopodobieństwa p = P(t>T-stat) jest nie większa od przyjętego poziomu istotności ( najczęściej przyjmujemy α = 0,05) to sprawdzaną hipotezę odrzucamy, czyli wartość oceny danego parametru jest istotnie różna od zera. Innymi słowy, jeżeli wszystkie wartości p w tablicy 3.2 są mniejsze od przyjętego poziomu istotności np. 0,05, to wszystkie zmienne uwzględnione w modelu są istotne.
Arkusz podsumowania opcji Regresja ułatwia również analizę reszt, której celem jest sprawdzenie wybranych założeń klasycznej metody najmniejszych kwadratów i rozstrzygnięcie dwóch podstawowych kwestii: czy postać analityczna modelu jest poprawna i czy uwzględniono w nim właściwe zmienne objaśniające. Do badania reszt możemy wykorzystać analizę graficzną na podstawie otrzymanych w arkuszu wykresów (rys 3.7, 3.8).
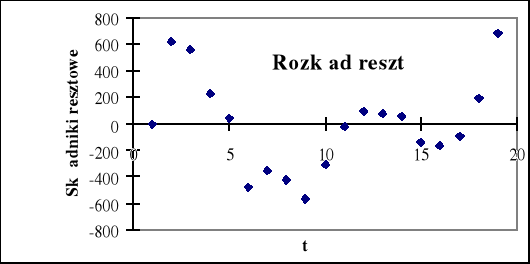
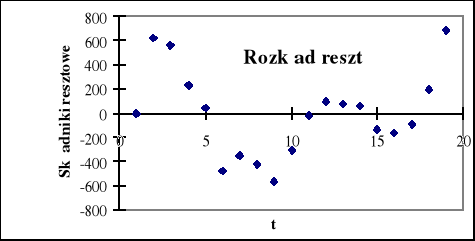
Rys. 3.7. Rozkład reszt
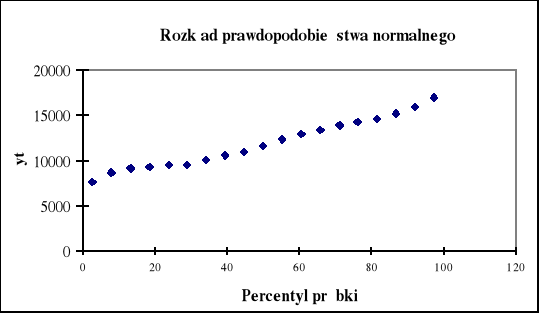
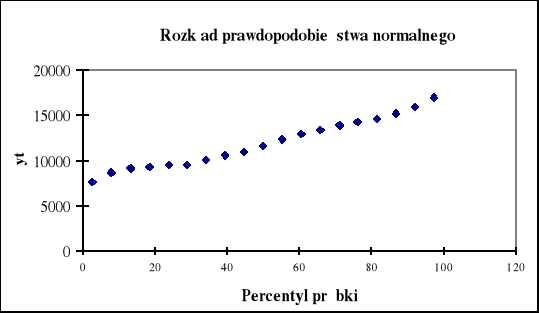
Rys. 3.8. Zgodność rozkładu reszt z rozkładem normalnym
Najprostszą charakterystyką poprawnego rozkładu reszt jest jego symetria, która oznacza równe prawdopodobieństwa występowania reszt ujemnych i dodatnich. Na rys. 3.7 liczba reszt dodatnich wynosi 9, a ujemnych -10, tak więc można przyjąć, że reszty te spełniają własność symetrii.
Kolejną własnością , którą według założeń winny spełniać reszty, jest ich losowość. Weryfikacja hipotezy o losowości ciągu reszt ma na celu ocenę trafności doboru postaci analitycznej funkcji regresji ( w przypadku modelu tendencji rozwojowej jest to wybór właściwej postaci analitycznej funkcji trendu ). Do weryfikacji hipotezy H0 : y = f(t) wobec hipotezy alternatywnej: H1: y ≠ f(t) służy tzw. test liczby serii.
Punktem wyjścia jest ciąg reszt uszeregowany według kolejności jednostek czasu. Dla tego uporządkowanego ciągu oblicza się liczbę serii reszt modelu - S. Serią jest każdy podciąg reszt złożony wyłącznie z elementów dodatnich lub ujemnych. Z tablic testu liczby serii dla danej liczby reszt dodatnich n1, liczby reszt ujemnych n2, oraz przyjętego poziomu istotności α ( tj. dla α/2 i 1-α/2) odczytuje się dwie krytyczne liczby serii: S1 i S2 . Jeśli:
S1 ≤ S ≤ S2,
to nie ma podstaw do odrzucenia hipotezy H0 . Oznacza to, że ciąg reszt jest losowy, wobec czego postać analityczna modelu została dobrana trafnie. Jeżeli liczba serii jest w przybliżeniu równa połowie liczby obserwacji, możemy być pewni, że reszty są losowe. W naszym przykładzie na rys. 3.7 widzimy 5 serii, więc bez skorzystania z tablic nie mamy pewności, jaką decyzję powinniśmy podjąć. Wykres reszt według następstwa czasowego pozwala również na ocenę jednorodności wariancji.
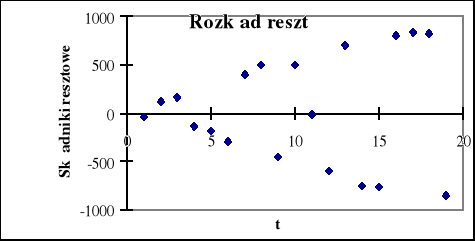
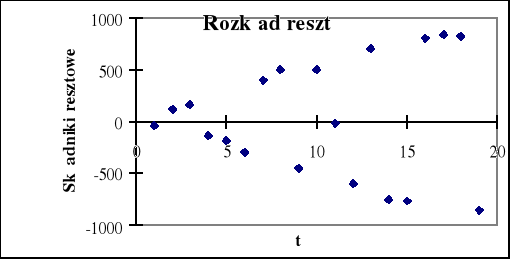
Rys. 3.9. Badanie stałości wariancji
Na rys. 1.9 wyraźnie widzimy że odchylenie standardowe reszt ( średnia odległość punktów wykresu od osi czasu) nie jest stałe w danym okresie, lecz wykazuje tendencję rosnącą, nie jest więc spełnione założenie o jednorodności wariancji.
W regresji wielorakiej zakłada się również, że wartości resztowe posiadają rozkład normalny. Wykres rozkładu prawdopodobieństwa normalnego (rys.1.8) pozwala na szybką wizualną ocenę zgodności reszt z rozkładem normalnym. Jeśli nie posiadają one rozkładu normalnego, to nastąpią odstępstwa od linii prostej. Na tym wykresie ujawnią się również obserwacje odstające (nietypowe).
1