1. Płyny, różnice między cieczami i gazami.

Substancje występujące w przyrodzie: ciała stałe, ciecze i gazy, składają się z drobin, które pozostają w nieustannym ruchu postępowym, obrotowym i drgającym. Miarą tego ruchu jest temperatura. Między drobinami występują siły wzajemnego oddziaływania - molekularne. Oddziaływanie tych sił zależy od stanu skupienia materii. Innym kryterium podziału ciał jest zmiana kształtu pod wpływem działania sił mechanicznych. Charakterystycznymi wielkościami fizycznymi płynów są ciśnienie, gęstość i temperatura.

Płyny dzielimy na ciecze i gazy:

• ciecze to płyny, które zachowują niemal stałą objętość pod działaniem nawet wielkich sił mechanicznych i małej zmianie temperatury (mała ściśliwość), przyjmują kształt zbiornika i są zdolne do formowania swobodnej powierzchni, zwanej zwierciadłem cieczy,

• gazy to płyny, które cechuje znaczna ściśliwość, zmieniają pod wpływem sił oraz temperatury swoją objętość, zaś wprowadzone do zamkniętego zbiornika zawsze wypełniają jego całą objętość.

2. Mechanika płynów i jej podział.

Przedmiotem mechaniki płynów są zjawiska ruchu i równowagi płynów ze szczególnym uwzględnieniem działania płynu na ścianki naczyń w których się znajduje lub ścianki ciał stałym, które opływa.

W mechanice płynów wyróżniamy następujące działy:

• statyka płynów - zajmująca się zagadnieniami równowagi płynów, nieruchomych względem układu odniesienia siłami wywieranymi przez płyny na ścianki naczyń lub na ścianki ciał stałych, które opływa,

• w dziale statyki wyróżniamy hydrostatykę, która zajmuje się tylko cieczami,

• kinematyka płynów zajmuje się ruchem płynów, bez uwzględnienia powodów wywołujących ruch,

• dynamika płynów - bada związki przyczynowe pomiędzy przyczyną wywołującą ruch, a skutkiem czyli ruchem,

• hydrodynamika - dotyczy wyłącznie cieczy, w dziale hydrodynamiki wyróżniamy dodatkowo hydraulikę, zajmującą się ruchem cieczy w przewodach rurowych oraz kanałach.

3. Hipoteza ciągłości d'Hamberta.

Płyn rzeczywisty złożony jest z wielkiej liczby poruszających się bezwładnie cząsteczek, co pozwala opisywać ciecz i gaz modelem ośrodka ciągłego z pominięciem przestrzeni i sił międzymolekularnych. Dla większości rozważanych zjawisk, ciągłości ośrodka towarzyszy ciągłość i różniczkowalność takich wielkości jak prędkość czy ciśnienie. Przedmiotem mechaniki cieczy i gazów są ośrodki ciągłe. Założenie ciągłości wprowadza jednak ograniczenia dotyczące najmniejszej objętości płynu, dla której cechy zawartego w niej ciała nie zmieniają się - czyli elementu płynu. Model ten zakłada, że nie ma przestrzeni między poszczególnymi elementami płynu, czyli cała objętość wypełniona jest płynem - jest to tzw. continuum materialne.

4. Definicja elementu płynu.

Element płynu jest to część masy płynu o wymiarach nieskończenie małych w porównaniu z wymiarami ścian ograniczających płyn lub ścian zamoczonych w płynie. Ta najmniejsza objętość musi jednak być dostatecznie wielka w porównaniu ze średnią drogą swobodną cząstek i zawierać dostateczną liczbę molekuł, aby można było stosować statystyczne metody uśredniania wielkości. Jednocześnie wymiary elementu płynu powinny być nieskończenie małe w stosunku do ciał stałych poruszających się lub ograniczających rozpatrywaną objętość płynu.

5. Właściwości fizyczne płynów.
   

W celu opisania zachowania się płynu pod wpływem sił niezbędne jest określenie parametrów charakteryzujących stan płynu oraz pewne własności fizyczne ośrodka. Indywidualne cechy każdego płynu zależą od temperatury oraz ciśnienia. Do podstawowych parametrów fizycznych płynu należą:

• gęstość to stosunek masy do objętości jaka ta masa zajmuje; wyróżniamy:

• gęstość średnią cieczy - definiowaną jako stosunek masy cieczy zawartej w pewnym obszarze do jego objętości (dla cieczy nieściśliwej) zgodnie ze wzorem:

;

• gęstość lokalną elementu cieczy uważanej za ośrodek ciągły - opisaną wzorem:

Gęstość zależy od ciśnienia i temperatury - woda zajmuje najmniejszą objętość w temperaturze 277 K, natomiast w temperaturach wyższych i niższych objętość jej wzrasta.

• ciężar objętościowy to stosunek ciężaru ciała do jego objętości, dla ciał niejednorodnych należy wyznaczyć granicę tego stosunku dla ΔV → 0, co opisuje wzór:

• ciężar objętościowy cieczy ściśliwej można wyrazić za pomocą zależności:

Ciężar objętościowy można również wyrazić zależnością:

γ = ρ * g [N/m³]

• lepkość cieczy jest to właściwość cieczy polegająca na stawianiu oporu przy wzajemnym przesuwaniu się cząstek względem siebie; właściwość ta występuje w cieczy będącej w ruchu i powoduje ujawnienie sił stycznych - sił oporów ruchu między wzajemnie przesuwającymi się cząsteczkami płynu. Wielkością charakteryzującą lepkość jest dynamiczny współczynnik lepkości. Zgodnie ze wzorem Newtona naprężenie jest proporcjonalne do pochodnej prędkości w kierunku normalnym do płaszczyzny występowania siły stycznej. Zjawisko lepkości najlepiej tłumaczy doświadczenie z dwoma równoległymi płytami, z których górna się przesuwa, a dolna pozostaje nieruchoma. Cząsteczki cieczy przylegające do płyty poruszają się z takimi samymi prędkościami co płyty. Siły tarcia występujące przy przesuwaniu warstw cieczy względem siebie określa zależność:

, zaś naprężenia styczne określa wzór:

; gdzie:

μ - dynamiczny współczynnik lepkości,

F - powierzchnia płynu.

V - objętość płynu.

W praktyce obok dynamicznego współczynnika lepkości znacznie częściej wykorzystuje się kinematyczny współczynnik lepkości, który opisuje wzór:

; gdzie:

ρ - gęstość cieczy,

• ściśliwość cieczy - jest to zdolność płynu do zmiany objętości w danej temperaturze przy zmianie ciśnienia. Jej miarą jest współczynnik ściśliwości opisywany zależnością:

; gdzie:

β_p - współczynnik określający względną zmianę objętości płynu przypadającą na jednostkę przyrostu ciśnienia, dla stałej temperatury ośrodka.

Odwrotnością współczynnika ściśliwości jest moduł sprężystości objętościowej K [Pa], stąd równanie można również zapisać jako:

• rozszerzalność cieplna płynu - to zdolność płynu do zmiany swej objętości przy danym ciśnieniu pod wpływem zmian temperatury. Własność tę opisuje współczynnik rozszerzalności cieplnej β_T, który definiuje zależność:

Współczynnik β_T wyraża względną zmianę objętości przypadającej na jednostkę przyrostu temperatury przy danym ciśnieniu płynu.

6. Modele płynów.

W celu ułatwienia matematycznego opisu zjawisk fizycznych w płynach w rozważaniach stosuje się często uproszczone modele cieczy i gazów. Uproszczenia polegają na pomijaniu niektórych własności fizycznych płynów rzeczywistych. W rozważaniach stosuje się następujące modele płynów:

• płyn nielepki w którym pomija się siły styczne podczas ruchu ośrodka - dynamiczny współczynnik lepkości wynosi 0,

• płyn nieściśliwy - w którym gęstość wynosi zero,

• ciecz doskonała, w której pomija się lepkość, ściśliwość, rozszerzalność cieplną oraz napięcie powierzchniowe,

• gaz doskonały, w którym pomija się objętość molekuł, siły spójności, lepkość. Gaz ten ściśle spełnia równanie stanu gazu Clapeyrona,

• gaz termodynamicznie doskonały, który spełnia równanie Clapeyrona, lecz jest ośrodkiem lepkim.

W większości zagadnień dotyczących stanu spoczynku płynu, rozwiązania dla płynów doskonałych są słuszne dla ośrodków rzeczywistych. W zagadnieniach ruchu wyników otrzymanych dla modeli uproszczonych nie można bezpośrednio przenieść na płyny rzeczywiste. W tym celu wp0rowadza się pewne współczynniki, których wartości są określone doświadczalnie.

7. Siły działające na płyny.

Rozróżnia się dwa rodzaje sił działających w danym obszarze płynu: siły masowe oraz siły powierzchniowe.

Siły masowe wynikają z oddziaływania zewnętrznego sił. Są one proporcjonalne do całej masy płynu. Można do nich zaliczyć siłę ciążenia, siły bezwładności i odśrodkowe wywołane ruchem naczynia z rozważanym płynem. Miarą sił masowych jest jednostkowa siła masowa F_jm - przypadająca na jednostkę masy rozważanego płynu. Ma ona wymiar przyspieszenia [m/s²], na przykład jednostkową siłą masową jest przyspieszenie ziemskie.

Siły powierzchniowe działają na powierzchni wydzielonej masy płynu i są proporcjonalne do tej powierzchni. Do sił powierzchniowych należy zaliczyć siły tarcia oraz parcia hydrostatycznego. Szczególnym rodzajem tych sił jest siła spowodowana napięciem powierzchniowym. Występuje ona na powierzchni ograniczającej dwa ośrodki.

Miarą sił powierzchniowych jest jednostkowa siła powierzchniowa F_jA, która jest granicą stosunku siły powierzchniowej do elementu powierzchni na którą działa.

Składowa jednostkowej siły powierzchniowej na kierunku normalnym do elementu powierzchni jest nazywana naprężeniem normalnym.

Dla płynu znajdującego się w stanie spoczynku, naprężenie normalne nazywane jest ciśnieniem. Dla poruszających się płynów ciśnieniem określa się średnią arytmetyczną z naprężeń normalnych działających w danym punkcie.

8. Zasada zesztywnienia, określenie ciśnienia hydrostatycznego.

Element cieczy poddawany działaniu sił pozostaje w równowadze, jeżeli suma ich rzutów na osie x, y, z przestrzennego układu współrzędnych jest równa 0.

Warunek ten zapisać można w postaci:

Σx = 0, Σy = 0, Σz = 0

Ciśnienie hydrostatyczne można określić na podstawie następującego toku rozumowania:

Zakładając, że pewna bryła cieczy zostanie przecięta wzdłuż płaszczyzny F i górna jej część odrzucona. Odrzuconą część bryły musimy zastąpić siłą parcia P, normalną do płaskiej powierzchni siłą ściskającą. Stosunek siły parcia do pola tej powierzchni nazywamy średnim ciśnieniem hydrostatycznym i zapisujemy równaniem:

P_śr =
[N/m²]

Natomiast ciśnienie w punkcie rozpatrywanego pola nazywamy granicą tego stosunku przy powierzchni pola malejącej do zera zgodnie z zależnością:

P = lim_ΔF→0
=
[N/m²] = [Pa]

9. Podstawowe twierdzenie hydrostatyki.

Jednym z podstawowych twierdzeń hydrostatyki jest twierdzenie Pascala. Mówi ono, ze jeżeli na ciecz pozostającą w spoczynku działają tylko siły powierzchniowe to ciśnienie hydrostatyczne w każdym punkcie ma stałą wartość. Prawo to udowadnia się w ten sposób, że wycina się z cieczy element w kształcie walca ograniczonego podstawami dF₁ i dF₂. Normalne powierzchnie walca dF_n tworzy z podstawami dF₁ i dF₂ kąty α₁ i α₂. Z zależności matematycznych wynika, że elementarne parcie dP₁ i dP₂ tworzą z osią y również odpowiednie kąty α₁ i α₂. na podstawę dF₁ działa elementarne parcie hydrostatyczne:

dP₁ = p₁ * dF₁

zaś na podstawę dF₂ działa parcie hydrostatyczne:

dP₂ = p₂ * dF₂

z warunku równoległości dla cieczy pozostających w spoczynku wynika, że suma sił na oś Y jest równa 0. Równanie przyjmuje wtedy postać:

dP₁ * cosα₁ + dP₂ * cosα₂ = 0

Uwzględniając w równaniu wyżej zapisane zależności otrzymamy:

p₁ * dF₁ * cosα₁ + p₂ * dF₂ * cosα₂ = 0

Ponieważ między powierzchnią normalną walca dF_n, z powierzchniami dF₁ i dF₂ zachodzą zależności trygonometryczne:

dF₁ * cosα₁ = dF_n oraz dF₂ * cosα₂ =dF_n

-p₁dF_n + p₂ * dF_n = 0

p₁ = p₂

Prawo zostało udowodnione.

10. Różniczkowe równanie równowagi płynów (równanie Eulera).

Prawo Eulera mówi, że jeżeli na ciecz znajdującą się w spoczynku działają siły powierzchniowe i masowe, to wielkość ciśnienia wywieranego na element powierzchni umieszczony w dowolnym punkcie cieczy nie zależy od orientacji tego elementu.

Siła masowa w praktyce hydrotechnicznej występuje bardzo często przede wszystkim jako siła ciężkości. Powoduje ona niejednostajność ciśnienia w cieczy będącej w spoczynku, np. cząstki położone głębiej unoszą na sobie cząstki wyżej położone, co powoduje wzrost ciśnienia w niżej położonych warstwach.

Aby określić wartość ciśnienia w dowolnym punkcie cieczy, wyodrębniamy z niej bardzo mały element w postaci prostopadłościanu i rozważamy warunek równowagi w przestrzennym układzie współrzędnych x, y, z.

Zakładamy, że na jedną ze ścian prostopadłych do osi x działa ciśnienia p, a na przeciwległa do niej oddaloną o dx działa ciśnienie p +
, parcie na ścianę c wynosi pdxdy, zaś siła masowa działająca w kierunku osi x jest równa axdm = adxdydzp, gdzie ax to składowa jednostkowej siły masowej, zaś dm to elementarna masa.

W sposób analogiczny określamy siły masowe w kierunku osi y i z. Warunek równowagi cieczy pozostającej w spoczynku uwzględniający sumę wszystkich sił równoległych do osi x zapisujemy jako:

pdydz - (p +
)dydz +axρdxdydz = 0

zatem:

= axρdx

Analogicznie należy zapisać ΣY = 0 oraz ΣZ = 0

= ayρdy

= azρdz

Ponieważ ciśnienie jest funkcją zmiennych x, y, z różnica tej funkcji musi być zapisana:

dp =
+
+

Ostatecznie po scałkowaniu równanie to można zapisać jako:

p = p_o + p

11. Równanie cieczy właściwej znajdującej się w polu sił ciężkości.

W praktyce najczęściej zdarza się szczególny przypadek równowagi cieczy kiedy jedyna działającą siłą masową jest siła ciążenia. Dla przyjętego układu współrzędnych składowej jednostkowej siły masowej wynoszą: X = 0, Y = 0 i Z = 0 co po podstawieniu do równania równowagi płynu pozwala uzyskać:

a stąd dla ρ = const:

p = ρgz + C

Stałą całkowania można określić z warunku brzegowego: z = 0, p = p₀ wtedy C = p₀, co po podstawieniu daje równanie:

p =p₀ + ρgz = p₀ + γz

Dla swobodnego zwierciadła cieczy, ciśnienie p₀ jest równe ciśnieniu atmosferycznemu.

Powyższy wzór wyraża jedną z najważniejszych zależności hydraulicznych, którą można sformułować następująco: ciśnienie w dowolnym punkcie cieczy równe jest ciśnieniu zewnętrznemu powiększonemu o iloczyn ciężaru objętościowego i głębokości tego punktu pod zwierciadłem wody.

12. Naczynia połączone.

Przy wypełnieniu cieczy jednorodnych naczynia połączonego następuje wyrównanie poziomów w obu ramionach naczynia. Przy założeniu, że ciśnienie panujące na powierzchniach swobodnych są jednakowe p₁ = p₂, ciśnienie hydrostatyczne na poziomie porównawczym w warunkach równowagi będą jednakowe z prawej i lewej strony naczynia zgodnie z równaniem:

p₁ + γh₁ = p₂ + γh₂

Z tego względu, że z założenia są jednakowe ciśnienia, jednakowe muszą być również poziomy cieczy - stąd pojawia się prawo:

W otwartych naczyniach połączonych wypełnionych jednorodną cieczą powierzchnie swobodne w obu ramionach znajdują się na tych samych poziomach.

Natomiast w przypadku różnych ciśnień panujących na powierzchniach swobodnych w obu częściach naczynia różnicę tych ciśnień mierzyć można poprzez różnicę poziomów cieczy w ramionach naczynia.

Naczynia połączone zawierające dwie różnorodne, nie mieszające się ciecze o ciężarach właściwych γ₁ i γ₂. Zakładając, że płaszczyzna tych dwu cieczy leży w poziomie porównawczym na głębokościach h₁ i h ₂ powierzchni swobodnych z lewej i prawej części naczynia; porównując ciśnienia w punktach leżących na tej płaszczyźnie w lewej i prawej części naczynia otrzymamy:

p₁ + γ₁h₁ = p₂ + γ₂h₂; przy założeniu, że p₁ = p₂ uzyskujemy:

γ₁h₁ = γ₂h₂ lub h₁/h₂ = γ₂/γ₁

W naczyniach połączonych stosunek wysokości słupów dwu nie mieszających się ze sobą cieczy ponad ich płaszczyznę styku jest równy odwrotnemu stosunkowi ich ciężarów właściwych. Prawo to ma zasadnicze znaczenie w konstrukcji manometrów.

13. Przyrządy do pomiaru ciśnienia.

Do pomiaru ciśnienia służą przyrządy, które można podzielić na trzy podstawowe grupy - piezometry, wakuometry i manometry.

Piezometr - to rurka szklana o średnicy wewnętrznej nie mniejszej niż 0,5 cm, otwarta u góry i połączone jednym końcem ze zbiorników wypełnionym cieczą będącą pod ciśnieniem zewnętrznym p_t>p_a. Piezometr służy do pomiaru nadciśnienia w cieczy wysokością słupa tejże cieczy. Mierząc wysokość słupa h_p cieczy w piezometrze obliczamy z równania równowagi ciśnienie bezwzględne na poziomie porównawczym od strony naczynia oraz od strony piezometru. Przyrównując obie te wartości uzyskujemy równanie:

p_b - p_a = γ(h_p - h₁) = γh

Manometr cieczowy - wykonany jest z rurki szklanej wygiętej w kształcie litery U, wypełnionej cieczą manometryczną o gęstości większej od gęstości płynu zbiorniku.

Jeden koniec ruruki połączony jest z naczyniem drugi jest otwarty i pozostaje pod działaniem ciśnienia atmosferycznego. Po połączeniu manometru z obszarem mierzonego ciśnienia ustala się stan równowagi. Ciśnienie panujace na powierzchni swobodnej zapisać możemy jako:

p_b = p_a + γ₁h₁ - γ(h+a)

Do pomiaru różnicy ciśnień w dwu różnych punkach służą manometry różnicowe. Najbardziej rozpowszechnione w praktyce technicznej są manometry różnicowe rtęciowe. Aby ustalić związek jaki zachodzi między wskaźnikami manometru a różnicą ciśnień w punktach A i B, przyjmujemy, że ciśnienia p_A > p_B.

Podstawiając to do ogólnego równania uzyskujemy:

p = p_A - p_B = h(γ₁ - γ)

Vakuometr służy do pomiaru podciśnienia, jest to wygięta rurka w kształcie litery U napełniona cieczą manometryczną, przeważnie rtęcią. Jeden koniec rurki łączymy z obszarem w którym ciśnienie jest mniejsze od ciśnienia atmosferycznego p_b < p_a, zaś drugi koniec jest otwarty i połączony z atmosferą.

14. Parcie cieczy na płaskie ścianki naczynia.

Parcie hydrostatyczne to siła z jaką ciecz będąca w stanie spoczynku oddziałuje na ścianki na dno zbiornika, na ciało zanurzone w cieczy lub na wyodrębnioną w niej powierzchnię. Parcie wywołane jest przez siły masowe (ciężar bezwładności oraz siły powierzchniowe) przyłożone do jednej z powierzchni ograniczającej objętość cieczy. Wartość parcia określa równanie definiujące ciśnienie:

dP = pdF = (pa + γh) dF

P =

Parcie hydrostatyczne jest prostopadłe do powierzchni działania I wyraża się w jednostkach siły.

Jedyną siłą masową działającą na ciecz jest siła ciężkości. Pole F dzieli się na elementarne poletka dF. Rozpatrywany element powierzchni dF znajduje się na głębokości h pod zwierciadłem cieczy. Zatem elementarne na nie parcie wyniesie:

dP = pdF + p_adF = γhdF + p_adF

Ponieważ wszystkie rozpatrywane elementy powierzchnie leżą w jednej płąszczyźnie to parcie elementarne działające prostopadle do tych poletek są względem siebie równoległe. Stąd wniosek, że parcie całkowite powierzchni F będzie sumą algebraiczną parć elementarnych i może być określone w drodze powyższego wyrażenia w obszarze F:

P =

Występująca w równaniu całka
wyraża moment statyczny pola F względem zwierciadła cieczy i może być zastąpiona przez iloczyn zagłębienia środka ciężkości pola F pod zwierciadłem wody i powierzchni tego pola F.

P = γh_sF + p_aF

Przy założeniu, że ciśnienie atmosferyczne działające na zwierciadło cieczy jest równoważone przez ciśnienie działające od zewnątrz na ścianę ostatecznie parcie na ścianki płaskie określa zależność:

P = γh_sF

Jeżeli natomiast na zwierciadło cieczy działa pewne nadciśnienie p_s, to jego wpływ na wielkość siły parcia możemy zastąpić przez zwiększenie zagłębienia h_s o wielkość wysokości tego nadciśnienia p_a/γ. Oznacza to, że umownie podnosimy zwierciadło cieczy o wielkość p_a/γ i przyjmujemy na tej podniesionej powierzchni nadciśnienie równe 0.

16. Graficzna metoda wyznaczania siły parcia działającej na ścianki płaskie.

Parcie można przedstawić również zgodnie z następującym wzorem:

P =

Sens geometryczny tej całki jest taki, iż wyraża ona objętość bryły, którą utworzymy odkładając w każdej elementarnej powierzchni dF odcinek do niej prostopadły i równy zagłębieniu tej powierzchni pod zwierciadłem wody. Tak skonstruowana bryła nosi nazwę bryły parcia. Jej objętość to całka: V =
.

Generalizując parcie na powierzchnię płaską jest równe liczbowo ciężarowi bryły parcia. Wykres parcia to pionowy przekrój brył parcia. Na ogół przekrojem są trójkąty, są jednak sytuacje, że przekrojem jest trapez.

17. Parcie na ścianki zakrzywione.

Parcie na ścianki zakrzywione można przedstawić jako sumę geometryczną wektorów parć składowych. Obliczenie parcia sprowadza się do znalezienia składowych tej siły na kierunkach osi współrzędnych układu.

Rozważając na przykład parcie cieczy na powierzchnię cylindryczną, aby wyznaczyć wektor parcia elementarnego można rozłożyć go na trzy składowe parcia P_x, P_y, P_z. Wtedy parcie całkowite będzie wynosiło:

P =

Założenia do rozważań są następujące:

• ciecz jest nieściśliwa,

• zbiornik otwarty i ciśnienie atmosferyczne.

Parcie rozkładamy na składowe równoległe do osi x,y,z.. Powierzchnię A dzielimy na elementarne pole powierzchni dA, na które działa elementarna siła dP prostopadła do dA. Elementarna siła dP rozłożona jest na elementarne składowe dP_x, dP_y oraz dP_z, nachylone do wektora parcie dP o kąty: α, β, γ. Wtedy składowe zapisać możemy jako:

dP_x = dP * cosα, dP_y = dP * cosβ, dP_z = dP * cosγ

Zakładając, że powierzchnia dA jest płaska, wówczas działającą siłę można określić jako:

dP = γ*z*dA; gdzie z - zagłębienie pod powierzchnią cieczy.

Podstawiając zależność do wszystkich pozostałych składowych otrzymujemy:

dP_x = γ*z*dA* cosα

dP_y = γ*z*dA* cosβ

dP_z = γ*z*dA* cosγ

Powstałe kąty dwuścienne między powierzchnia rzutów dA_x, dA_y oraz dA_z są równe:

dA_x/dA = cosα

dA_y/dA = cosβ

dAz/dA = cosγ

Otrzymaliśmy w ten sposób składowe elementarne parcia jako:

dP_x = γ*z*dA_x, dP_y = γ*z*dA_y, dP_z = γ*z*dA_z

Rozpatrując całą powierzchnię, którą podzielono na małe części to elementarne składowe będą względem siebie równoległe. Dlatego można je zsumować arytmetycznie.

Otrzymujemy w ten sposób wzory na składowe parcia na powierzchnię zakrzywioną:

P_x =
= γ*z_scx*A_x

P_y =
= γ*z_scy*A_y

P_z =
= γ*V

W przypadku ostatniej całki V jest to objętość pionowego słupa cieczy, od dołu ograniczonego powierzchnią zakrzywiona A, a od góry płaszczyzną zwierciadła.

18. Prawo Archimedesa.

Na ciało całkowicie lub częściowo zanurzone w cieczy działają siły parcia hydrostatycznego oraz siła ciężkości. Rozpatrując parcie cieczy na ciało zanurzone można zauważyć, że poziome składowe parcia wzajemnie się znoszą. W celu obliczenia parcia pionowego należy podzielić bryłę na dwie części poziomą płaszczyzną. Sporządzając wykresy parcia na górną i dolną powierzchnię, i po ich złożeniu można stwierdzić, że bryła wypadkowego parcia pionowego pokrywa się z bryłą ciała zanurzonego. Wypadkowa siła parcia pionowego skierowana jest ku górze i jest nazywana wyporem .

Jeżeli objętość zanurzonej części ciała wynosi V, a gęstość cieczy ρ wtedy wypór jest równy:

W = ρ*g*V

W przypadku cieczy jednorodnej, punkt zaczepienia siły wyporu znajduje się w geometrycznym środku zanurzonej części ciała. Wypór działa przeciwnie do ciężaru ciała, co powoduje pozorna utratę przez zanurzone ciało części jego ciężaru. Zjawisko to znane jest jako prawo Archimedesa. Ciało zanurzone w cieczy znajduje się w równowadze, jeżeli jego ciężar G jest równy wyporowi W, a siły te leżą na wspólnej osi pionowej nazywanej osią pływania.

Ciało tonie, gdy G>W. Jeżeli G<W ciało jest częściowo zanurzone, a siła wyporu W, równa ciężarowi G jest odniesiona jedynie do objętości zanurzonej części ciała.

19. Kinematyka cieczy - ogólne pojęcia.

Kinematyka zajmuje się badaniem geometrycznych właściwości ruchu, bez analizy przyczyn wywołujących ten ruch. Podstawowymi pojęciami kinematyki są czas i przestrzeń. Ruch płynu określa się, podając dla każdego elementu jego położenia prędkość oraz chwilowe przyspieszenie. Prędkość przemieszczania się dowolnego elementu płynu składa się w ogólnym przypadku z prędkości unoszenia, prędkości wynikłej z obrotu elementu względem chwilowej osi oraz prędkości deformacji.

Do podstawowych pojęć dotyczących ruchu cieczy zaliczyć możemy:

• tor cząstki cieczy - linia, jaką wyznacza poruszająca się w przestrzeni pojedyncza cząstka cieczy,

• smuga - miejsce geometryczne wszystkich cząstek, które przeszły przez określony punk przestrzeni,

• prędkość - stosunek drogi poruszającej się cząstki do czasu, w jakim tę drogę przebyła,

• struga elementarna - to pęk linii prądu o nieskończenie małym przekroju poprzecznym - jest to pojęcie fizyczne, ponieważ posiada wszystkie wymiary, nieskończenie mały przekrój strugi pozwala na założenie, że w całym jej przekroju ciśnienie i prędkość są wielkościami stałymi,

• rurka prądu - to linie prądu tworzące pobocznicę strugi,

• strumień to zbiór strug, jakie przepływają przez przekrój o wymiarach skończonych.

20. Strumień pola prędkości.

Ponieważ w przekroju strumienia parametry hydrauliczne jak prędkość, ciśnienie mogą ulegać zmianom, w praktycznych obliczeniach operuje się średnimi wartościami tych parametrów. Jest to zasada jednowymiarowego traktowania przepływu. Pojęcia takie jak linia prądu, struga, strumień związane są z polem prędkości.

Podstawowymi wielkościami zwanymi parametrami ruchu cieczy opisującymi ruch dowolnej cząsteczki w dowolnym czasie są:

• prędkość poruszających się poszczególnych cząstek cieczy,

• przyspieszenie - zmiana prędkości w czasie,

• ciśnienie panujące w dowolnym punkcie cieczy.

21. Prawo zachowania masy płynącej.

Zasada zachowania masy jest stosowana w mechanice płynów w postaci równania ciągłości przepływu. Zgodnie z tą zasadą przez każdy przekrój strumienia przepływa jednakowa ilość cieczy.

Można to zapisać następującym wzorem:

v₁ * F₁ = v₂ * F₂

lub Q₁ = Q₂ = Q - objętościowe natężenie w jednym przekroju jest równe objętościowemu natężeniu w drugim przekroju.

Prawo to można dla wyodrębnionego w przestrzeni poruszającego się płynu obszaru V ograniczonego zamkniętą powierzchnią płynną, wyrazić równaniem:

m =
=const

Oznaczając przez A₁ powierzchnię przez którą płyn dopływa, przez A₂ tę przez którą płyn wypływa można równanie zapisać jako:

= M [kg/s]

Dla płynu nieściśliwego można zapisać:

= Q [m³/s]

Innymi słowy w ruchu ustalonym płynu nieściśliwego wydatek wpływający do objętości kontrolnej jest równy wydatkowi wypływającemu.

22. Doświadczenie Reynoldsa. Prędkość graniczna.

Przepływ płynu o określonym polu prędkości i ciśnienia musi być stateczny. Przepływ jest stateczny, jeżeli wytworzone w nim drobne zaburzenie z czasem wygasa. Przepływ jest niestateczny, gdy zaburzenie to z czasem będzie narastać. Pierwsze badania stateczności ruchu cieczy lepkich przeprowadził Reynolds obserwując przepływu wody przez rurkę szklaną, do której równocześnie była doprowadzana struga barwnika. Przy małych natężeniach przepływu zabarwiona struga płynie wzdłuż osi rury tworząc prostoliniową smugę. Przy większych prędkościach przepływu smuga ta zaczyna oscylować, tworząc linię falistą. Dalsze zwiększenie prędkości wywołuje nagłe, intensywne mieszanie się obu cieczy.

Na podstawie omówionych tu doświadczeń Reynolds wprowadził podział przepływów na dwa zasadnicze rodzaje: przepływ laminarny i turbulentny. Przejście z ruchu laminarnego w turbulentny występuje przy pewnej wartości bezwymiarowego wyrażenia - liczby Reynoldsa:

Re =
; gdzie:

d - średnica rurociągu,

v_sr - prędkość średnia

υ - kinematyczny współczynnik lepkości.

Przejście od ruchu laminarnego do turbulentnego w przewodzie kołowym jest możliwe dla warunków, w których wartość liczby Reynodlsa zawiera się w granicach 2320 < Re < 50000. wartość Re = 50000 to górna krytyczna wartość liczby Reynoldsa, a wartość Re = 2320 to dolna krytyczna wartość Re.

Ruch laminarny i turbulentny możemy również różnicować na podstawie prędkości granicznej. v_gr = (2320 - 50000)
.

Gdy stosunek v/v_gr < 1 wówczas mamy do czynienia z ruchem laminarnym, zaś gdy v/v_gr > 1 wtedy występuje ruch burzliwy; v/v_gr = 1 - jest to prędkość graniczna.

23. Metody badania ruchu płynów.

Do podstawowych metod pomiaru ruchu płynów zaliczamy metody wykorzystujące następujące urządzenia:

• rurkę Pitota,

• zwężką Venturiego,

• dysze i kryzy dławiące.

Rurka Pitota służy do pomiaru prędkości przepływającego strumienia. Strumień przepływający przez przekrój przewodu, napotyka przeszkodę, w postaci zakrzywionej pod kątem prostym rurki (litera L) i wpada do niej. Rurka jest zakończona manometrem, w którym znajduje się ciecz manometryczna. Panujące ciśnienie dynamiczne w strumieniu, związane z jego prędkością, powoduje wychylenie się cieczy manometrycznej w rurce - ΔH, proporcjonalne do prędkości przepływającej cieczy:

, na tej podstawie określamy prędkość przepływającego strumienia ze wzoru: v =
.

Zwężka Venturiego służy do pomiaru wydatku - natężenia przepływu w przewodach. Jest to przewód kołowy o stałym przekroju z wbudowanym współosiowo krótkim odcinku o mniejszym przekroju i łagodnym przejściu.

Pisząc dla zwężki równaniu Bernuliego uzyskujemy:

bez uwzględnienia strat energii. Korzystając z równania zachowania masy otrzymujemy:

v₁ * F₁ = v₂ * F₂ = Q - zatem v₂ = (F₁/F₂) * v₁; v₂ = m*v₁

Do zwężki zamontowane są dodatkowo dwie rurki piezometryczne - przed i w miejscu zwężenia, które wskazują różnicę ciśnień ΔH (ciśnienie mniejsze występuje w węższym przekroju).

Na tej podstawie - wiedząc, że ΔH =
otrzymujemy wzór na prędkość przepływu:

V₁ =
, stąd wiedząc, że Q = v₁ * F₁ otrzymujemy wzór pozwalający obliczyć objętościowe natężenie przepływu:

Q = F₁
, zaś chcąc uwzględnić straty wprowadzić należy współczynnik poprawkowy k, wtedy wzór przyjmie postać: Q = k*F₁
.

Kryzy i dysze - służą do pomiarów wydatków w przewodach kołowych. Są to przeszkody pierścieniowe zamontowane na przekroju rurociągu, do których za i przed przeszkodą zamontowano jeszcze rurki piezometryczne.

Wydatek przepływającej wody można określić za pomocą wzoru:

Q = α*F₁
= c
, gdzie stała c - jest ustalana doświadczalnie na drdze cechowania - kalibracji dyszy lub kryzy.

Natomiast współczynnik α określa wzór: α =

25. Wypływ cieczy przez otwory.

Ciecz wypływająca przez otwór - np. w ścianie lub dnie zbiornika, może poruszać się ruchem ustalonym bądź nieustalonym. Wypływ jest ustalony, gdy parametry ruchu nie zmieniają się w czasie. Otwory mogą być niezatopione, gdy cieczy wypływa swobodnie do przestrzeni gazowej, oraz zatopione, gdy ciecz przepływa między zbiornikami, a otwór jest usytuowany poniżej obu zwierciadeł cieczy. Dla otworów niezatopnionych można wprowadzić podział na otwory małe i duże. Jeżeli różnice prędkości w najwyższym i najniższym punkcie otworu jest mała w stosunku do prędkości średniej, to otwór taki będzie traktowany jako mały. Otwory nie spełniające tego warunku są nazywane dużymi. Przy tym podziale nie mają znaczenia wymiary otworu, lecz wartość stusnku wysokości otworu h do wysokości zagłębienia środka ciężkości otworu ponizej swobodnego zwierciadła cieczy w zbiorniku. Podział taki nie jest istotny w stosunku do otworów zatopionych, gdyż prędkość wypływu cieczy dla otworów zatopionych zależy wyłącznie od różnicy poziomów zwierciadeł cieczy i jest praktycznie taka sama w każdym punkcie otworu.

Dla otworów małych wyznaczony na podstawie równania Bernuliego wzór określający średnią prędkość przepływu wygląda następująco:

v = α
; gdzie

α - jest to współczynnik prędkości określony ze wzoru α =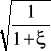
; gdzie znajdujący się w mianowniku wyrażenia ξ - to współczynnik oporów miejscowych,

H₀ - suma wysokości słupa cieczy nad środkiem otworu i różnicy ciśnień gazu nad cieczą w zbiorniku i poza nim.

Aby określić wydatek małego otworu należy przemnożyć prędkość przez pole powierzchni tego otworu. Uzyskamy wtedy wzór:

Q = βαA
; gdzie:

A - pole powierzchni otworu,

β - współczynnik kontrakcji strumienia.

Iloczyn współczynników β*α = μ - otrzymujemy współczynnik wydatku.

Stąd stosowany w praktyce wzór dla wypływu cieczy przez małe otwory:

Q = μA
[m³/s]

Dla otworów dużych należy uwzględnić różne prędkości, które narastają wraz z zagłębieniem punktu otworu pod swobodnym zwierciadłem cieczy. W analizie ustalonego wypływu cieczy przez otwór duży będzie rozpatrzony układ w którym otwór umieszczony jest w ścianie zbiornika nachylonej do poziomu pod kątem. Dla obliczenia wydatku Q należy podzielić otwór na elementarne poziome paski o wysokości dz. Każdy z takich pasków jest otworem małym, o powierzchni dA = y dz/ sinα. Szerokość otworu Y jest funkcją zagłębienia: y = y(z). Jeżeli pominie się energię prędkości opadania cieczy w zbiorniku, (v₁ = 0), wtedy prędkość wypływu cieczy ze szczeliny zagłębionej o z pod swobodnym zwierciadłem w zbiorniku wyniesie:

v = α

Elementarny wydatek dQ jest równy v*dA, zaś całkowity wydate Q otworu jest sumą wydatków elementarnych i wynosi:

Q =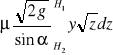

Współczynnik wydatku charakteryzuje pracę całego otworu. Współczynnik tej jest zmienny podobnie jak przy otworach małych. Jego orientacyjna wartość wynosi ok. 0,6.

26. Współczynniki α, β, γ.

Wzajemne korelacje liczbowe pomiędzy wymienionymi współczynnikami określa wzór:

β*α = μ

Współczynnik α - jest to współczynnik uwzględniający straty lokalne przepływu. Można określić go wzorem:

α =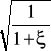
; gdzie znajdujący się w mianowniku wyrażenia ξ - to współczynnik oporów miejscowych,

Współczynnik β - określa stopień dławienia, bądź inaczej kontrakcji strumienia. Wskutek działania sił bezwładności poszczególne strugi cieczy dopływające do otworu z różnych kierunków wywołują przewężenie strumienia. Stąd przekrój rzeczywisty strumienia jest mniejszy od przekroju otworu. W pewnej odległości od otworu strugi zaczynają płynąć równolegle, a prędkości i ciśnienia w całym przekroju zwężonego strumienia A_s wyrównują się. Stosunek A_s do A jest nazywany współczynnikiem dławienia - kontrakcji (Stosunek przekroju zwężonego strumienia do pola otworu, przez który następuje wypływ cieczy).

Współczynnik wydatku μ - określony jest doświadczalnie i zależy od kształtu i jakości krawędzi otworu, położenia otworu względem ścian zbiornika oraz jego zagłębienia pod zwierciadłem cieczy. Dla otworów kołowych współczynnik ten zmienia się od 0,59 do 0,63, w zależności od średnicy i zagłębienia otworu (ze wzrostem zagłębienia współczynnik wydatku nieznacznie maleje).

27. Wypływ cieczy przez otwór zatopiony.

W przypadku wypływu cieczy przez mały otwór zatopiony należy rozważyć równanie Bernuliego dla dwóch poziomów cieczy znajdujących się po przeciwnych stronach przegrody.

Równanie to wygląda następująco:

z₁ +

Suma strat występująca na końcu wyrażenia uwzględnia opory miejscowe na wlocie do otworu oraz przy nagłym rozszerzeniu przekroju za otworem. Jest ona odniesiona do prędkości przepływu cieczy przez zatopiony otwór.

Po przekształceniu równania Bernuliego otrzymujemy wzór na prędkość przepływu cieczy przez otwór:

v =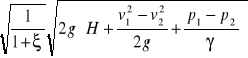

Dokonując podstawień:

α =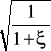
; β*α = μ, oraz H_o =
otrzymujemy:

v = α
; oraz Q = μA
[m³/s]

Należy zwrócić uwagę, że dla otworów zatopionych prędkość v jest jednakowa we wszystkich punktach otworu, gdyż różnica położenia zwierciadeł H jest taka sama dla tych punktów. Traci więc sens podział otworów zatopionych na małe i duże.

Wartość współczynnika wydatku μ_z dla otworu zatopionego jest nieco mniejsza od wartości μ dla otworu zatopionego.

μ_z = 0,986μ

28. Wypływy przez przystawki.

Wartość współczynnika wydatku μ może być zmieniana przez umieszczenie w otworze przystawki. Jest to krótka rura, najczęściej w kształcie walca lub stożka ściętego, mocowana do zewnętrznej lub wewnętrznej ścianki zbiornika. Wymiary przystawki powinny być tak dobrane, aby ciecz wypływała z niej pełnym przekrojem. Na przykład długość przystawki walcowej nie może być mniejsza od 3 średnic otworu wylotowego. Strumień przewęża się po wpłynięciu do przystawki, a następnie stopniowo rozszerza, całkowicie wypełniając przekrój wylotowy przystawki. W zwężonym przekroju strumienia występuje większa prędkość niż na wylocie z przystawki, stąd ciśnienie jest tam mniejsze od zewnętrznego. Powstanie dodatkowej różnicy ciśnień wpływa na wzrost współczynnika wydatku otworu. Opory ruchu na długości przystawki nieznacznie zmniejszają wartość μ. Zastosowanie przystawki walcowej zwiększa współczynnik wydatku otworu pod warunkiem, że wypływ odbywał się całym jej przekrojem. Dla przystawek walcowych zewnętrznych, mocowanych na zewnętrz otworu zbiornika, współczynnik μ zawiera się w granicach 0,68 - 0,82. większe wartości współczynnika wydatku otrzymuje się dla przystawki stożkowej zbieżnej.

29. Czas napełniania i opróżniania zbiornika przez mały otwór.

W celu wyznaczenia czasu opróżniania zbiornika t rozpatrzony będzie układ otwartego zbiornika o zmiennym przekroju i początkowym napełnieniu H, który jest opróżniany przez otwór o powierzchni A_o i współczynniku wydatku μ. W pewnej chwili zwierciadło cieczy wzniesione jest na wysokość z ponad otworem, z powierzchnia zwierciadła będzie równa A_z. Po czasie dt zwierciadło obniży się o wartość dz. Dla tego czasu można przyjąć, że wydatek Q nie ulegnie zmianie i wynosi:

Q = μA
,

Porównując objętość cieczy, jaka przepłynęła przez otwór w czasie dt, z objętością o jaką zmniejszy się zawartość naczynia, można napisać:

Qdt = -A_zdz

Znak minus oznacza ubytek cieczy w naczyniu (ze wzrostem czasu t maleje wysokość z). Przekształcając to równanie ze względu na dt, po podstawieniu zależności na wydatek Q, otrzymuje się:

dt = -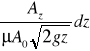

Czas obniżenia się swobodnego zwierciadła cieczy do pewnej wysokości z_k wynosi

T =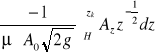

Przed wykonaniem całkowania należy określić zależność A_z = A_z (z). Współczynnik wydatku jest średnią z wartości μ określanych dla z = H i z = z_k

34. Równanie Bernuliego dla cieczy doskonałej.

Założenia dla wyprowadzenia równania:

• ciecz jest doskonała,

• ruch cieczy jest ustalony i ciągły,

• rozpatrujemy strugę cieczy,

• jedyną siłą masową będzie siła ciężkości - działająca na ciecz.

W cieczy doskonałej nie występuje lepkość, dlatego ruch odbywa się bez strat energetycznych. Masa cieczy podlega zasadzie zachowania energii.

Należy rozpatrzyć odcinek strugi zawartej pomiędzy dwoma przekrojami.

W całym przekroju 1 zarówno prędkość, jak i ciśnienie są identyczne - w każdym punkcie przekroju. Strumień będący w ruchu po jakimś czasie przedostaje się do przekroju drugiego, w którym również w każdym punkcie ciśnienie i prędkość są identyczne.

Całkowity przyrost energii układu jest równy sumie prac wykonywanych przez siłę zewnętrzną działającą na ten układ:

ΔF = L_p

Podstawową siłą występującą w układzie jest siła parcia, której praca zmienia energię całkowitą układu (energię kinetyczna i potencjalną)

Praca w przekroju pierwszym (siła x przesunięcie):

L_p1 = p₁*dF₁*dl₁ = p₁ * dV₁

Praca w przekroju drugim jest skierowana przeciwnie, zatem:

L_p2 = -p₂ * dF₂ * dl₂ = p₂ * dV₂

Zatem całkowita praca w układzie jest równa:

L_p = (p₁ - p₂) * dV

Praca ta powoduje zmiany energii potencjalnej I kinetycznej które wynoszą:

• dla energii potencjalnej: Δ(m*b*y) = ρ * dV * g (y₂-y₁); gdzie wyrażenie y₂ - y₁ to położenie środków ciężkości przekrojów w stosunku do poziomu porównawczego,

• dla energii kinetycznej: Δ
  

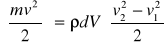
Zatem równanie bilansu energetycznego będzie miało postać:

(p₁ - p₂) * dV = ρ * dV * g (y₂-y₁) +
; dzieląc całość przez wyrażenie ρdVg uzyskujemy równanie Bernuliego dla cieczy doskonałej, które ma postać:

y₁ +
= y₂ +
= E; gdzie:

y₁ - odległość środka ciężkości od poziomu porównawczego,

- wysokość ciśnienia piezometrycznego [m]

- wysokość prędkości [m]

Ze względu na fakt, iż w każdym przekroju jest założona stała prędkość, a w rzeczywistości tak nie jest, został wprowadzony współczynnik korygujący ten błąd, a mianowicie współczynnik Coriolissa przy wielkości prędkości. Waha się on w granicach 1,01 - 1,07 i oznacza symbolem α, w wyrażeniu:
po prawej i lewej stronie równania.

35. Interpretacja geometryczna równania Bernoulliego dla cieczy doskonałej.

Polega ona na odłożeniu na wykresie wszystkich składników równania Bernoulliego, a mianowicie sumy wysokości położenia, ciśnienia i prędkości przekroju strugi cieczy doskonałej w ruchu ustalonym w jednorodnym polu grawitacyjnym, która jest wielkością stałą. Suma ta nazywana jest wysokością energii i nie zmienia się wzdłuż danej strugi linia wzdłuż osi strugi nazywana jest linią położenia. Linia znajdująca się na wysokości z + p/γ ponad poziomem odniesienia jest nazywana linią ciśnienia. Suma wszystkich trzech składników równania tworzy linię energii. Dla cieczy doskonałej linia energii jest prostą poziomą.

36. Spadek i spad hydrauliczny.

Spadek hydrauliczny to straty ciśnienia odniesione do jednostki długości. Są one wprost proporcjonalne do prędkości przepływającej cieczy. Te dwa elementy wiąże ze sobą zależność:

J = k * vⁿ; gdzie:

J - spadek hydrauliczny,

V - prędkość przepływu,

k - współczynnik proporcjonalności,

n - wykładnik potęgowy charakteryzujący rodzaj ruchu.

Spadek hydrauliczny jest również definiowany często jako pochylenie linii energii, czyli inaczej wielkość strat energii do długości odcinka.

37. Równanie Bernoulliego dla cieczy lepkiej.

W cieczy lepkiej występują opory tarcia. Praca sił tarcie powoduje, że suma trzech członów wysokości energii E równania Bernoulliego nie jest stała, becz maleje wzdłuż strumienia. Różnica energii między dwoma przekrojami strumienia 1 i 2 jest nazywana wysokością strat ciśnienia i oznaczana symbolem h_s.

Równanie Bernoulliego dla strumienia cieczy rzeczywistej między przekrojami 1 i 2 ma postać:

y₁ +
= y₂ +
+ h_s

Podobnie jak pozostałe człony równania, wysokość strat ciśnienia h_s jest określona w metrach słupa cieczy w przewodzie. We wzorze występują średnie prędkości przepływu. Z tego względu uwzględniono również współczynniki prędkości - α.

y₁ +
= y₂ +
+ h_s

Linia energii obniża się w kierunku przepływu wskutek oporów tarcia. Piezometryczna linia ciśnień opada, lecz przy spadku prędkości średniej wywołanym wzrostem przekroju poprzecznego strumienia A, także może się wznosić. Straty ciśnienia obejmują straty liniowe, proporcjonalne do długości odcinka, oraz straty miejscowe, powstałe w wyniku lokalnego zaburzenia przepływu np. w armaturze przewodu. Równania Bernoulliego i ciągłości oraz wzory określające straty liniowe i miejscowe są wykorzystywane do praktycznych obliczeń parametrów ustalonego przepływu cieczy rzeczywistej.

38. Straty hydrauliczne między przekrojami i różnica naporu.

Straty hydrauliczne możemy generalnie podzielić na straty liniowe i miejscowe.

Pierwsze z nich nazywane też oporami liniowymi, oblicza się ze wzoru Darcy'ego - Weisbacha. Wysokość tych strat jest równa stosunkowi spadku ciśnienia do ciężaru właściwego strumienia:

h_L =
; gdzie:

λ - współczynnik oporów liniowych,

L - długość odcinka przewodu miedzy dwoma przekrojami,

D - średnica przewodu,

v - prędkość przepływu cieczy przez przewód.

Wzór ten określony został dla kołowego przekroju strumienia. Dla niekołowych przekrojów straty ciśnienia określa się wykorzystując pojęcie promienia hydraulicznego R_h. Wówczas wzór określający straty ciśnienia wygląda następująco:

h_L =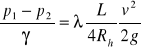
.

Występujący w tych wzorach współczynnik oporów liniowych λ w ruchu ustalonym jest w ogólnym przypadku funkcją liczby Reynoldsa i chropowatości względnej ε wewnętrznej powierzchni przewodu: λ = λ(Re; ε); gdzie

Re =
; zaś

Chropowatość bezwzględna k zależy od średniej wysokości nierówności, ich kształtu i rozmieszczenia na powierzchni ścianki ograniczającej strumień.

Straty miejscowe to lokalne zaburzenia wywołane zmianą kierunku ruchu, gwałtownym rozszerzeniem bądź zwężeniem, dzieleniem lub łączeniem strumieni. Zaburzenia te rozpraszają część energii strumienia. Wysokość strat ciśnienia przy przepływie płynu przez przeszkody lokalne oblicza się ze wzoru:

h_M =
.

Współczynnik ξ - to współczynnik oporu miejscowego. Zależy od rodzaju przeszkody, parametrów geometrycznych charakteryzujących daną przeszkodę, jak stopień otwarcia zaworu, promień krzywizny i kąt zmiany kierunku przepływu, a także od liczby Reynoldsa. Wartości współczynnika oporów miejscowych dla poszczególnych przeszkód są w większości przypadków trudne do ustalenia na drodze teoretycznej.

Różnica naporów dwóch oddalonych od siebie przekrojów może być wyznaczona na podstawie zależności:

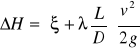
39. Współczynnik oporów liniowych - wykres Moody.

W zakresie przepływu laminarnego współczynnik λ zależy tylko od liczby Reynoldsa. W ruchu turbulentnym współczynnik ten może zależeć zarówno od liczby Reynoldsa, jak i od chropowatości względem ścianki przewodu ε. Szerokie badania wpływu chropowatości na współczynnik oporów liniowych przeprowadził Nikuradse. W doświadczeniach tych zastosowano rury mosiężne o średnicy D. Późniejsze badania współczynnika oporów liniowych dotyczyły głównie rur o chropowatości technicznej k, zależnej od technologii produkcji i rodzaju materiału oraz czasu eksploatacji. Przy doborze współczynnika oporów liniowych szerokie zastosowanie znajduje nomogram Colebrooka - White'a. Nomogram ten jest zalecany do obliczania współczynnika lambda. Każda krzywa na tym wykresie odpowiada innej chropowatości względnej przewodu. Z analizy nomogramu wynika, że:

• dla Re < 2320 na rysunku znajduje się linia prosta będąca wykresem zależności:

- spełnioną dla ruchu laminarnego,

• dla 2320 < Re < 4000, wobec zmiennego charakteru ruchu, wartości współczynnika oporów lokalnych nie są określone - jest to strefa gwałtownego wzrostu współczynnika oporów liniowych,

• dla Re > 4000 można wyróżnić trzy strefy:

• linia najniżej położona wyznacza strefę rur hydraulicznie gładkich. W strefie tej przyścienna warstwa laminarna przykrywa nierówności ścianki. Współczynnik oporów liniowych zależy tylko od Re i jest opisany wzorem Prandtla - Karmana - zaś w obliczeniach praktycznych wykorzystuje się wzór Blasiusa:

;

• obszar położony powyżej i ograniczony z prawej strony linią Re_gr nosi nazwę strefy przejściowej. W strefie tej, przyścienna warstwa laminarna tylko częściowo przykrywa nierówności ścianki, stąd współczynnik oporów linowych zależy od Re oraz chropowatości,

• obszar na prawo od linii Re_gr nazywa się strefą kwadratowej zależności oporów. W strefie tej współczynnik lambda zależy tylko od chropowatości względnej, a jego wartość oblicza się ze wzoru Prandtla - Nikurasego. Wzór ten był opracowany dla rur o zastępczej chropowatości piaskowej d = k zgodnie z badaniami Nikurasego.

40. Wykres równania Bernouliego dla cieczy rzeczywistej.

Linia ciśnień w przypadku cieczy rzeczywistej opada w kierunku przepływu wskutek oporów tarcia. Piezometryczna linia ciśnień opada również, lecz przy spadku prędkości spowodowanej wzrostem przekroju poprzecznego strumienia A, może się również wznosić. Straty ciśnienia obejmują straty liniowe, proporcjonalne do długości odcinka, oraz straty miejscowe, powstałe w wyniku lokalnego zaburzenia przepływu. Patrz załączony rysunek.

41. Obliczenia rurociągów hydraulicznych o przekroju kołowym (zadania).

Do obliczeń związanych z projektowaniem rurociągów najważniejsze są trzy typy zadań:

Typ	Wyznaczamy	Zadane
I		Q, l, d, k, ξ, υ
II	Q	, l, d, k, ξ, υ
III	d	, Q, d, k, ξ, υ

Typ I i III to zadania typowo projektowa, natomiast typ I - eksploatacyjne.

Pierwszy typ zadania polega na obliczeniu różnicy naporów jako przyczyny przepływu, spadku naporu hydraulicznego. Na podstawie podanych w tabeli danych obliczamy różnicę naporów zgodnie z zależnością:

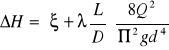
W tym celu należy obliczyć liczbę Reynoldsa oraz współczynnik chropowatości zgodnie ze wzorami: Re =
; zaś

Na podstawie obliczonych wartości odczytujemy z wykresu Moody współczynnik oporów liniowych. W sytuacji, gdy wyznaczony współczynnik chropowatości bezwzględnej nie znajdzie się dokładnie na jednej z linii wykresu należy interpolować wartość pomiędzy.

Drugi typ zadań wiąże się z określeniem przepływu Q. Wymaga on poczynienia założenia, że ruch odbywa się w strefie V na wykresie Moody, - czyli strefie kwadratowej zależności oporów. W strefie tej krzywe są liniami prostymi, które zależą tylko od współczynnika chropowatości względnej: λ = λ(ε).

Na podstawie odczytanej wielkości λ = λ(ε) przekształcamy wzór na straty ciśnienia i obliczamy przepływ: Q₁ =

Dla wyznaczonego przepływu Q₁ obliczamy liczbę Reynoldsa, a następnie odczytujemy λ₂ = λ(Re, ε). Na podstawie odczytanego drugiego współczynnika obliczamy wartość przepływu Q₂.

Następnie porównujemy przepływ Q₁ i Q₂:

; gdzie δ to założony błąd.

W sytuacji, gdy wartość błędu jest większa od założonej, należy powtórzyć obliczenia, wyliczając dla Q₂ liczbę Re₂ i odczytując z wykresu Moody wartość λ₃, dla której wyznaczyć należy dalej Q₃.

I tak do skutku.

Trzeci typ zadań wyznaczamy obierając kilka dowolnych średnic d i podstawiając do wzoru na straty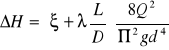
. Następnie po obliczeniu trzech, czterech wartości straty naporu dla założony średnic d_1, d₂, d₃, d₄ rysujemy wykres w którym na osi x zaznaczamy średnicę, zaś dla osi y zaznaczamy straty hydrauliczne.

Mając dane ΔH bierzemy wielkość strat naporu i nanosimy na wykres otrzymujemy średnicę. Przy czym wyznaczoną w ten sposób średnicę należy zaokrąglić w górę i przyjąć pierwszą średnicę znormalizowaną.

42. Charakterystyka pojedynczego przewodu. Charakterystyka przewodów połączonych.

W rozważaniach uwzględniamy przewody długie czyli takie które charakteryzują się niewielką liczbą oporów miejscowych. Taki warunek spełniają sieci wodociągowe, rozdzielcze. Dla tej sytuacji straty lokalne, miejscowe są małe w porównaniu ze stratami na długości. Wtedy pomija się straty lokalne, uwzględniając je jako współczynnik strat liniowych. Jeżeli znamy straty dla długości przewodu to możemy zapisać straty liniowe jako:

H_{str l} =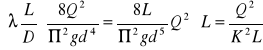

Współczynnik K - nazywamy przepuszczalnością przewodu - która zależy od średnicy przewodu. Zaś wyrażenie R = (L/K²) nazywać będziemy naporem hydraulicznym.

Zależność między wysokością strat ciśnienia a natężeniem przepływu Q będziemy nazywać charakterystyką przepływu. Charakterystyka przepływu w V strefie przepływu jest parabolą wychodzącą z początku układu współrzędnych.

Dobierając dowolną ilość Q podstawiamy je do wzoru i obliczamy straty naporu, nanosimy na wykres i otrzymujemy charakterystykę przepływu. Charakterystyki te wykorzystuje się do rozwiązywania różnych zadań, całek oraz parametrów hydraulicznych.

Przewody można łączyć szeregowo oraz równolegle. Pierwszy typ połączenia przewodów występuje wtedy, gdy koniec pierwszego wykresu jest jednocześnie początkiem drugiego. Punkty w których łączą się te rurociągi to węzły.

W połączeniu szeregowym straty naporu na poszczególnych odcinkach sumują się.

Zadania hydrauliczne można rozwiązywać dodając w sposób graficzny poszczególne charakterystyki przewodów - uzyskując w ten sposób charakterystykę zastępczą.

Z równania ciągłości przepływu dla rurociągów połączonych szeregowo wynika, że Q₁ = Q₂ = Q₃.

W połączeniu równoległym przewodów straty hydrauliczne na poszczególnych odcinkach są jednakowe. Zgodnie z równaniem ciągłości przepływu Q = Q₁ + Q₂ + Q_3.

Również rozwiązując zadania z rurociągami połączonymi równolegle należy rozwiązywać graficznie sumując charakterystyki pojedynczych rurociągów i określając charakterystykę zastępczą.

43. Ustalony przepływ cieczy ze swobodnym zwierciadłem w kanałach otwartych i korytach sztucznych.

Do przewodów ciśnieniowych zalicza się koryta naturalne i sztuczne, a także przewody zamknięte. Lecz niecałkowicie wypełnione cieczą. Ciecz płynąca w tych kanałach tworzy swobodne zwierciadło. Ze względu na kształt przekroju wyróżnia się koryta pryzmatyczne o niezmiennym na długości kształcie (trapezowe, trójkątne, prostokątne), kanały o rosnącym lub malejącym przekroju w kierunku przepływu, a także koryta naturalne o nieregularnym obrysie przekroju. Ruch cieczy wywołany nachyleniem - spadkiem podłużnym kanału i jest nazywany przepływem grawitacyjnym. Przepływ grawitacyjny może odbywać się ruchem jednostajnym lub niejednostajnym. Przepływ niejednostajny dzieli się na ruch wolnozmienny i szybkozmienny. Przepływ jednostajny jest ruchem ustalonym podczas, gdy pozostałe przepływy mogą być ustalone lub nieustalone. Najprostszym ruchem jest ruch jednostajny, w którym strumień o stałym natężeniu przepływu Q ma stały przekrój poprzeczny A i jednakowe głębokości napełnienia h na długości kanału. Stałe napełnienie oznacza jednocześnie równoległość zwierciadła cieczy do dna koryta.

Warunkiem koniecznym istnienia ruchu jednostajnego jest stały przekrój poprzeczny strumienia o niezmienne na długości szorstkości dna i brzegów koryta. Z warunkiem tym wiąże się równoległość linii zwierciadła wody oraz dna koryta.

Średnią prędkość przepływu wody w korycie wyznacza wzór:

v =

gdzie c =

Objętościowe natężenie przepływu można określić zgodnie z zależnością:

Q = v * A =

Wzory Chezy'ego oraz Manninga umożliwiają obliczanie strat hydraulicznych na długości koryta otwartego. Obliczanie współczynnika C z zależności gdzie współczynnik oporów liniowych zależy od liczby Reynoldsa oraz chropowatości względnej, umożliwia stosowanie wzoru Chezy w całym zakresie zmienności liczby Reynoldsa.

44. Kanały otwarte o przekroju trapezowym.

Danymi do obliczania przekroju trapezowego są:

B - szerokość kanału,

B - szerokość dna,

m - nachylenie skarpy kanału = ctgα

α - nachylenie do poziomu,

h - napełnienie kanału.

Mając parametry geometryczne kanału można określić przede wszystkim przekrój - liczony jako:

A = (b + m*h) * h

Oraz obwód zwilżony liczony jako suma wszystkich boków kanału, zwilżanych płynącą wodą określony wzorem:

U = b + 2h
.

Znając pole powierzchni oraz obwód zwilżony można określić promień hydrauliczny jako iloraz :

R_h = A/U

NA tej podstawie można określić przepływ wody przez kanał określony wzorem:

Q =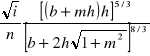

Dla przekrojów trapezowych wyróżnimy następujące typy zadań:

Typ	Szukane	Zadane
1	Q	b, n, i, h, m
2	h	b, n, i, Q, m
3	i	b, n, h, Q, m
4	b	n, i, h, Q, m

Rozwiązania typów są następujące:

• typ pierwszy - rozwiązujemy zgodnie z podanym powyżej wzorem,

• typ drugi - zakładamy dowolne h, podstawiamy i obliczamy Q i porównujemy z wielkością zadanego Q, następnie zwiększamy, lub zmniejszamy h, aby otrzymać Q zadane,

• typ trzeci - z przekształcenia wzoru,

• typ czwarty - metodą prób i błędów podstawiamy dowolne b i obliczamy Q - tak długo, aż osiągniemy wielkość zadaną.

45. Kanały otwarte o przekroju trójkątnym.

Danymi do obliczenia kanału trójkątnego są:

B - szerokość korony kanału,

b - szerokość dna = 0,

h - napełnienie,

m - nachylenie skarp

Szerokość korony kanału określa wzór: B = 2*m*h - na podstawie tej wielkości możemy określić pole przekroju kanału jako:

A = m * h²

Obwód zwilżony wyniesie zatem:

U = 2h

Wyznaczony na tej podstawie przepływ :

Q =

46. Kanały otwarte o przekroju kołowym

Dla kanału o przekroju kołowym natężenie przepływu określa wzór Chezy - Manninga.

W przypadku, gdy przepływ odbywa się pewnym wycinkiem kanału rozważanie jest następujące:

• określamy pole wycinka kanału:
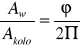
  czyli A_w =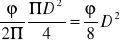
  ,

• określamy pole przekroju przez który przepływa ciecz, równe: A =
  ,

• określamy obwód zwilżony równy: U =
  ,

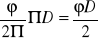
• określamy promień hydrauliczny jako stosunek pola powierzchni przekroju do obwodu zwilżonego równy: R_h =
  

• na tej podstawie ze wzorów Chezy - Maninnga można określić natężenie przepływu oraz prędkość liczone jako:

Q =

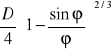
v = Q/A =

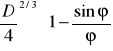
47. Wykresy Adrianiniego. Metoda bezwymiarowych parametrów.

Metoda ta polega na wyprowadzeniu bezwymiarowych parametrów. Jednym z takich właśnie parametrów jest stosunek napełnienia kanału do szerokośc idna: a = h/b. Parametr ten wstawiamy do pola przekroju i promienia hydraulicznego (dla przekrojów trapezowych).

Wtedy: A = b² (1 + ma)a zaś U = b (1 + 2

Wyznaczony w ten sposób promień hydrauliczny wyniesie:

R_h =
, a przepływ Q =

Na tej podstawie można określić dwie strony równania, w którym jedna zależy wyłącznie od bezwymiarowego parametru a oraz nachylenia skarp m:

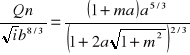
Z wykresu Adrianiniego dla znanego nachylenia skarp oraz wyznaczonego czynnika po lewej stronie równania można określić stosunek a/b i na tej podstawie obliczyć głębokość napełnienia koryta.

Analogiczny tok rozumowania obowiązuje w przypadku wyznaczania szerokości dna koryta, z tym wyjątkiem, że równanie wykorzystane do wykresu Adrianiniego wygląda wtedy następująco:

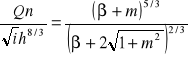
; gdzie „beta” to odwrotność wyznaczonego powyżej współczynnika a =
.

Podobne wykresy można sporządzić dla przekroju trójkątnego i kołowego - ich skala to skala logarytmiczna.

48. Krzywa sprawności dla kanału kołowego.

Obliczenia parametrów przepływu wykonuje się, wykorzystując krzywe sprawności przekroju kanału.

Wzory Chezego na wydatek i prędkość podane w punktach wcześniejszych można zapisać jako v = W
=

; gdzie:

β - współczynnik sprawności przekroju, równy ilorazowi prędkości w kanale przy częściowym i całkowitym napełnieniu,

W₀ - charakterystyka prędkości, równa średniej prędkości przepływu cieczy przy całkowitym napełnieniu przewodu i spadku dna równym jedności.

Q = K
=

; gdzie:

α - współczynnik sprawności przekroju, równy ilorazowi wydatku w kanale prze częściowym i całkowitym napełnieniu kanału,

K - przepuszczalność przewodu dla przepływu przy całkowitym napełnieniu przewodu i spadku równym jedności.

Współczynniki sprawności odczytuje się z krzywych sprawności przekroju w funkcji h/H, dla określonego kształtu przewodu. Krzywe te tworzy się dla poszczególnego rodzaju przekroju - inne dla przekroju trapezowego, inne dla kołowego.

49. Ruch podkrytyczny i nadkrytyczny, prędkość krytyczna.

W korycie otwartym linia energii jest wzniesiona ponad linię zwierciadła cieczy o wartość czynnika prędkości: v²/2g. Przy założeniu stałego wydatku Q = const., całkowita energia w danym przekroju zmienia się w funkcji napełnienia kanału. Można zauważyć, że:

• dla h dążącego do 0; A też dąży do zera, zaś energia dąży do nieskończoności,

• zaś dla h dążącego do nieskończoności, A też dąży do nieskończoności, i energia dąży do nieskończoności.

Istnieje więc taka głębokość dla której energia ma wartość minimalną. Głębokość taką nazywa się krytyczną, a odpowiadający jej ruch - ruchem krytycznym.

Kryterium ruchy krytycznego określa zależność:

Dla dodatniej wartości Q musi istnieć taka głębokość h, dla której natężenie przepływu Q osiąga wartość maksymalną.

Innym kryterium określającym ruch krytyczny jest liczba Frude'a opisana zależnością:

Fr =
= 1 - wtedy mamy do czynienia z ruchem krytycznym. Gdy liczba Frude,a jest mniejsza od jedności ruch jest podkrytyczny, gdy większa nadkrytyczny.

Ruch krytyczny jest pewnym szczególnym przypadkiem przepływu jednostajnego i w naturze samoistnie nie występuje. Stanowi on natomiast granicę między obszarami ruchu rwącego Fr>1 i spokojnego Fr<1. Jeżeli głębokość jest mniejsza od głębokości krytycznej w korycie występuje ruch rwący. W tym przypadku liczba Fr jest większa od jedności. W ruchu rwącym udział energii kinetycznej rośnie, obniża się zaś energia potencjalna. Dla h>h_kr przepływ cieczy odbywa się ruchem spokojnym, czyli Fr < 1. Obniżaniu się energii kinetycznej towarzyszy wzrost energii potencjalnej strumienia. Dominującymi siłami są siły grawitacyjne. Ruch spokojny występuje dla odpowiednio małego nachylenia dna koryta.

50. Kryteria rozróżniania charakteru ruchu.

Rodzaj występującego w korycie ruchu można określić na podstawie:

• analizy równania kryterialnego ruchu krytycznego:
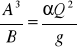
  . Jeżeli lewa strona tej zależności jest mniejsza od prawej, to w korycie panuje ruch rwący. Relacja odwrotna odpowiada przepływowi spokojnemu ,

• wartości liczby Frude'a,

• porównania parametrów przepływu (głębokości napełnienia, spadku, prędkości) z odpowiadającymi im wielkościami krytycznymi (v_kr, i_kr, h_kr).

---