Wydział Zarządzania |
Imię i Nazwisko 1. Marcin Zbroiński 2. Piotr Zając |
ROK IIB |
GRUPA 4 |
ZESPÓŁ 2 |
|||
Pracownia Fizyczna |
Temat: Mostek Wheatstone'a |
Nr ćw. 32 |
|||||
Data wykonania 1998-04-23 |
Data oddania 98-05-06 |
Zwrot do poprawy |
Data oddania |
Data zaliczenia |
|
||
I. Cel ćwiczenia
Pomiar nieznanych oporów oraz ich połączeń szeregowych i równoległych. Wskazanie statycznego wyniku pomiarów dla wybranego oporu.
II. Wprowadzenie
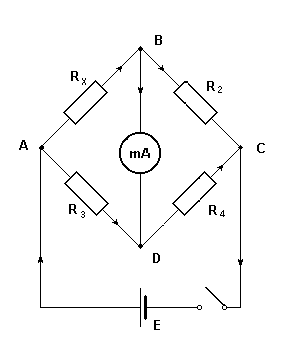
Mostek Wheatstone'a jest układem do pomiaru (porównywania) oporów. Tworzy go połączenie czterech oporów: Rx, R2, R3,R4 oraz galwanometru o oporze R5. Mostek jest zasilany z ogniwa galwanicznego lub zasilacza.

rys. Oporowy mostek Wheatstone`a
Niech I oznacza natężenie prądu płynącego z ogniwa, a natężenia prądów w odcinkach obwodu AB, AD, BC, DC, i BGD odpowiednio: I1, I2, I3, I4, I5. W układzie są 4 węzły A, B, C, D. Dla trzech z nich układa się równania Kirchoffa. Jeśli kierunek prądu jest taki, jak wskazują strzałki, dla węzłów A, B i D otrzymujemy:
A: I - I1 - I3 = 0
B: I1 - I2 -I5 = 0 (1)
D: I5 +I3 -I4 = 0
Drugi układ równań Kirchoffa można ułożyć wydzielając w schemacie zamknięte obwody ABDA, BCDB i ACEA. Obchodząc każdy z tych obwodów według kierunku wskazówek zegara otrzymujemy dla obwodu:
ABDA: I5Rx + I5R5 - I3R3 = 0
BCDB: I2R2 + I4R4 - I5R5 = 0 (2)
ACEA: I3R3 + I4R4 + IRE = ![]()
Jeśli dana jest siła elektromotoryczna ![]()
oraz opory R2, R3,R4 i RE, można znaleźć natężenia wszystkich sześciu prądów I, I1, I2, I3, I4, I5.
Metoda Wheatstone'a porównywania oporów polega na tzw. równoważeniu mostka, to znaczy na takim dopasowaniu oporów, by potencjały w punktach B i D były równe (VB = VD), czyli żeby prąd płynący przez galwanometr G był równy zeru. Przy I5 = 0 drugie i trzecie równanie układu (1) dają:
I2 = I1 I3 = I4 (3)
a pierwsze i drugie równanie układu (2)
I1Rx = I3R3 I2R2 = I4R4. (4)
Z równań (3) i (4) wynika, że
Ostatnie wyrażenie pozwala eksperymentalnie wyznaczyć Rx.
Mostek Wheatstone'a używany w ćwiczeniu przedstawiono na rysunku .
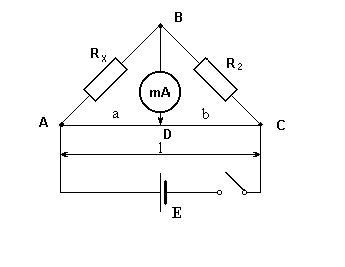
Prąd płynący z ogniwa galwanicznego E rozgałęzia się w punkcie A. Jedna jego część płynie przez szeregowo połączone opory Rx i R2, druga przez przewód AC. Przez zmiany położenia punktu D zmienia się stosunek oporów R3 do R4. Na odcinku BGD prąd nie będzie płynął, jeżeli
Ponieważ RAD i RDC są oporami odcinków tego samego jednorodnego drutu, ich wielkości są proporcjonalne do długości:
Ponadto b jest różnicą całkowitej długości drutu l i odległości a, b=l-a. Ostatecznie otrzymujemy:
Dokładność pomiaru mostkiem Wheatstone'a z drutem oporowym zależy przede wszystkim od błędu wyznaczenia odległości a. Zgodnie z prawem przenoszenia błędu:
(5)
Tak więc błąd pomiaru będzie najmniejszy gdy pochodna wyrażenia (5) będzie równa 0:
Rozwiązanie a=1/2 l odpowiada po uwzględnieniu drugiej pochodnej minimalnej wartości błędu. Tak więc aby pomiar był najdokładniejszy należy tak dobrać opór R2, aby stan równowagi mostka można było uzyskać w przybliżeniu w połowie długości drutu oporowego.
III. Wyniki pomiarów i opracowanie wyników
Pomiary wstępne
Długość drutu ![]()
100cm
Błąd pomiaru długości drutu ![]()
Napięcie zasilania ![]()
Opracowanie wyników
Odchylenie standardowe dla stu pomiarów :
Błąd dla sześciu pomiarów z rozstępu (liczba pomiarów mniejsza niż 10):
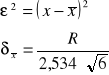
Pomiary dla pierwszego rezystora RX1
Lp. |
a [cm] |
b [cm] |
R2
[ |
RX1
[ |
|
1 |
50,00 |
50,00 |
10,00 |
10,00 |
3,52 10-1 |
2 |
45,80 |
54,20 |
12,00 |
10,14 |
2,05 10-1 |
3 |
43,80 |
56,20 |
13,00 |
10,13 |
2,13 10-1 |
4 |
42,20 |
57,80 |
15,00 |
10,95 |
1,28 10-1 |
5 |
39,00 |
61,00 |
18,00 |
11,51 |
8,37 10-1 |
6 |
36,30 |
63,70 |
19,00 |
10,83 |
5,48 10-2 |
Wartość średnia |
|
10,59 [ |
Błąd |
|
2,43 10-1 [ |
Pomiary dla pierwszego rezystora RX2
Lp. |
a [cm] |
b [cm] |
R2
[ |
RX2
[ |
|
1 |
50,20 |
49,80 |
20,00 |
20,16 |
9,22 10-4 |
2 |
47,90 |
52,10 |
22,00 |
20,23 |
1,26 10-3 |
3 |
44,80 |
55,20 |
25,00 |
20,29 |
9,77 10-3 |
4 |
43,00 |
57,00 |
27,00 |
20,37 |
3,15 10-2 |
5 |
42,20 |
57,80 |
28,00 |
20,44 |
6,35 10-2 |
6 |
40,40 |
59,60 |
29,00 |
19,66 |
2,84 10-1 |
Wartość średnia |
|
20,19 [ |
Błąd |
|
1,27 10-1 [ |
Pomiary dla połączenia szeregowego rezystorów RX1 i RX2
Lp. |
a [cm] |
b [cm] |
R2
[ |
R
[ |
|
1 |
43,00 |
57,00 |
40,00 |
30,18 |
5,53 10-4 |
2 |
41,90 |
58,10 |
42,00 |
30,29 |
8,14 10-3 |
3 |
41,30 |
58,70 |
43,00 |
30,25 |
3,01 10-3 |
4 |
39,10 |
60,90 |
47,00 |
30,18 |
5,41 10-4 |
5 |
43,60 |
56,40 |
39,00 |
30,15 |
2,50 10-3 |
6 |
44,90 |
55,10 |
37,00 |
30,15 |
2,33 10-3 |
Wartość średnia |
|
30,20 [ |
Błąd |
|
2,26 10-2 [ |
Wartość teoretyczną obliczam ze wzoru na połączenie szeregowe dwóch rezystorów
![]()
=30,78
Porównując wartość średnią z wartością teoretyczną obliczam
![]()
0,58 [![]()
]
Pomiary dla połączenia równoległego rezystorów RX1 i RX2
Lp. |
a [cm] |
b [cm] |
R2
[ |
R
[ |
|
1 |
52,00 |
48,00 |
6,00 |
6,50 |
7,04 10-3 |
2 |
48,40 |
51,60 |
7,00 |
6,57 |
3,25 10-4 |
3 |
45,10 |
54,90 |
8,00 |
6,57 |
1,43 10-4 |
4 |
42,30 |
57,70 |
9,00 |
6,60 |
1,96 10-4 |
5 |
39,80 |
60,20 |
10,00 |
6,61 |
7,49 10-4 |
6 |
37,70 |
62,30 |
11,00 |
6,66 |
5,27 10-3 |
Wartość średnia |
|
6,58 [ |
Błąd |
|
2,52 10-2 [ |
Wartość teoretyczną obliczam ze wzoru na połączenie równoległe dwóch rezystorów
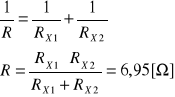
Porównując wartość średnią z wartością teoretyczną obliczam
![]()
0,37[![]()
]
Wyznaczenie krzywej rozkładu
Lp. |
a [cm] |
b [cm] |
R2
[ |
RX3
[ |
|
1 |
49,30 |
50,70 |
30,00 |
29,2 |
3,96 10-05 |
2 |
48,40 |
51,60 |
31,00 |
29,1 |
7,71 10-3 |
3 |
47,60 |
52,40 |
32,00 |
29,1 |
9,33 10-3 |
4 |
46,90 |
53,10 |
33,00 |
29,1 |
3,39 10-4 |
5 |
46,10 |
53,90 |
34,00 |
29,1 |
7,32 10-3 |
6 |
45,50 |
54,50 |
35,00 |
29,2 |
3,01 10-3 |
7 |
44,80 |
55,20 |
36,00 |
29,2 |
2,71 10-3 |
8 |
44,10 |
55,90 |
37,00 |
29,2 |
5,91 10-4 |
9 |
43,50 |
56,50 |
38,00 |
29,3 |
8,34 10-3 |
10 |
42,80 |
57,20 |
39,00 |
29,2 |
2,73 10-4 |
11 |
42,30 |
57,70 |
40,00 |
29,3 |
2,52 10-2 |
12 |
41,70 |
58,30 |
41,00 |
29,3 |
2,58 10-2 |
13 |
41,10 |
58,90 |
42,00 |
29,3 |
2,02 10-2 |
14 |
40,50 |
59,50 |
43,00 |
29,3 |
1,07 10-2 |
15 |
40,00 |
60,00 |
44,00 |
29,3 |
2,82 10-2 |
16 |
39,40 |
60,60 |
45,00 |
29,3 |
8,49 10-3 |
17 |
38,90 |
61,10 |
46,00 |
29,3 |
1,47 10-2 |
18 |
38,40 |
61,60 |
47,00 |
29,3 |
1,78 10-2 |
19 |
38,00 |
62,00 |
48,00 |
29,4 |
6,45 10-2 |
20 |
37,50 |
62,50 |
49,00 |
29,4 |
5,51 10-2 |
21 |
37,00 |
63,00 |
50,00 |
29,4 |
3,99 10-2 |
Lp. |
a [cm] |
b [cm] |
R2
[ |
RX3
[ |
|
22 |
36,60 |
63,40 |
51,00 |
29,4 |
7,64 10-2 |
23 |
36,10 |
63,90 |
52,00 |
29,4 |
4,49 10-2 |
24 |
35,70 |
64,30 |
53,00 |
29,4 |
6,80 10-2 |
25 |
35,30 |
64,70 |
54,00 |
29,5 |
8,81 10-2 |
26 |
34,80 |
65,20 |
55,00 |
29,4 |
3,63 10-2 |
27 |
34,00 |
66,00 |
57,00 |
29,4 |
3,93 10-2 |
28 |
33,30 |
66,70 |
59,00 |
29,5 |
8,44 10-2 |
29 |
32,50 |
67,50 |
61,00 |
29,4 |
4,21 10-2 |
30 |
31,80 |
68,20 |
63,00 |
29,4 |
4,41 10-2 |
31 |
31,10 |
68,90 |
65,00 |
29,3 |
3,04 10-2 |
32 |
30,50 |
69,50 |
67,00 |
29,4 |
5,64 10-2 |
33 |
29,90 |
70,10 |
69,00 |
29,4 |
7,05 10-2 |
34 |
29,30 |
70,70 |
71,00 |
29,4 |
6,71 10-2 |
35 |
28,70 |
71,30 |
73,00 |
29,4 |
4,80 10-2 |
36 |
28,20 |
71,80 |
75,00 |
29,5 |
8,50 10-2 |
37 |
27,70 |
72,30 |
77,00 |
29,5 |
1,12 10-1 |
38 |
27,10 |
72,90 |
79,00 |
29,4 |
4,09 10-2 |
39 |
26,60 |
73,40 |
81,00 |
29,4 |
3,57 10-2 |
40 |
26,10 |
73,90 |
83,00 |
29,3 |
2,21 10-2 |
41 |
25,70 |
74,30 |
85,00 |
29,4 |
5,56 10-2 |
42 |
25,20 |
74,80 |
87,00 |
29,3 |
2,10 10-2 |
43 |
24,80 |
75,20 |
89,00 |
29,4 |
3,45 10-2 |
44 |
24,50 |
75,50 |
91,00 |
29,5 |
1,33 10-1 |
45 |
24,10 |
75,90 |
93,00 |
29,5 |
1,33 10-1 |
46 |
23,70 |
76,30 |
95,00 |
29,5 |
1,18 10-1 |
47 |
23,40 |
76,60 |
97,00 |
29,6 |
2,18 10-1 |
48 |
23,10 |
76,90 |
99,00 |
29,7 |
3,29 10-1 |
49 |
22,70 |
77,30 |
101,00 |
29,7 |
2,44 10-1 |
50 |
22,30 |
77,70 |
103,00 |
29,6 |
1,57 10-1 |
51 |
80,40 |
19,60 |
7,00 |
28,7 |
2,03 10-1 |
52 |
78,20 |
21,80 |
8,00 |
28,7 |
2,19 10-1 |
53 |
76,10 |
23,90 |
9,00 |
28,7 |
2,58 10-1 |
54 |
74,20 |
25,80 |
10,00 |
28,8 |
1,65 10-1 |
55 |
72,30 |
27,70 |
11,00 |
28,7 |
2,06 10-1 |
56 |
70,50 |
29,50 |
12,00 |
28,7 |
2,38 10-1 |
57 |
68,80 |
31,20 |
13,00 |
28,7 |
2,49 10-1 |
58 |
67,10 |
32,90 |
14,00 |
28,6 |
3,75 10-1 |
59 |
65,60 |
34,40 |
15,00 |
28,6 |
3,14 10-1 |
60 |
64,10 |
35,90 |
16,00 |
28,6 |
3,56 10-1 |
61 |
62,70 |
37,30 |
17,00 |
28,6 |
3,47 10-1 |
62 |
61,40 |
38,60 |
18,00 |
28,6 |
2,84 10-1 |
63 |
60,00 |
40,00 |
19,00 |
28,5 |
4,43 10-1 |
64 |
58,90 |
41,10 |
20,00 |
28,7 |
2,54 10-1 |
65 |
57,70 |
42,30 |
21,00 |
28,6 |
2,70 10-1 |
66 |
56,50 |
43,50 |
22,00 |
28,6 |
3,49 10-1 |
67 |
55,60 |
44,40 |
23,00 |
28,8 |
1,32 10-1 |
Lp. |
a [cm] |
b [cm] |
R2
[ |
RX3
[ |
|
68 |
54,50 |
45,50 |
24,00 |
28,7 |
1,75 10-1 |
69 |
53,50 |
46,50 |
25,00 |
28,8 |
1,61 10-1 |
70 |
52,50 |
47,50 |
26,00 |
28,7 |
1,84 10-1 |
71 |
51,50 |
48,50 |
27,00 |
28,7 |
2,45 10-1 |
72 |
50,60 |
49,40 |
28,00 |
28,7 |
2,35 10-1 |
73 |
49,90 |
50,10 |
29,00 |
28,9 |
7,90 10-2 |
74 |
49,20 |
50,80 |
30,00 |
29,1 |
1,21 10-2 |
75 |
48,30 |
51,70 |
31,00 |
29,0 |
4,16 10-2 |
76 |
47,60 |
52,40 |
32,00 |
29,1 |
9,33 10-3 |
77 |
46,90 |
53,10 |
33,00 |
29,1 |
3,39 10-4 |
78 |
46,10 |
53,90 |
34,00 |
29,1 |
7,32 10-3 |
79 |
45,50 |
54,50 |
35,00 |
29,2 |
3,01 10-3 |
80 |
44,80 |
55,20 |
36,00 |
29,2 |
2,71 10-3 |
81 |
44,10 |
55,90 |
37,00 |
29,2 |
5,91 10-4 |
82 |
43,50 |
56,50 |
38,00 |
29,3 |
8,34 10-3 |
83 |
42,80 |
57,20 |
39,00 |
29,2 |
2,73 10-4 |
84 |
42,20 |
57,80 |
40,00 |
29,2 |
1,51 10-3 |
85 |
41,60 |
58,40 |
41,00 |
29,2 |
1,61 10-3 |
86 |
41,00 |
59,00 |
42,00 |
29,2 |
4,47 10-4 |
87 |
40,50 |
59,50 |
43,00 |
29,3 |
1,07 10-2 |
88 |
39,90 |
60,10 |
44,00 |
29,2 |
2,12 10-3 |
89 |
39,40 |
60,60 |
45,00 |
29,3 |
8,49 10-3 |
90 |
38,80 |
61,20 |
46,00 |
29,2 |
3,64 10-6 |
91 |
38,40 |
61,60 |
47,00 |
29,3 |
1,78 10-2 |
92 |
38,00 |
62,00 |
48,00 |
29,4 |
6,45 10-2 |
93 |
37,40 |
62,60 |
49,00 |
29,3 |
1,20 10-2 |
94 |
36,90 |
63,10 |
50,00 |
29,2 |
5,48 10-3 |
95 |
36,50 |
63,50 |
51,00 |
29,3 |
2,24 10-2 |
96 |
36,00 |
64,00 |
52,00 |
29,3 |
7,17 10-3 |
97 |
35,60 |
64,40 |
53,00 |
29,3 |
1,76 10-2 |
98 |
35,20 |
64,80 |
54,00 |
29,3 |
2,82 10-2 |
99 |
34,80 |
65,20 |
55,00 |
29,4 |
3,63 10-2 |
100 |
34,40 |
65,60 |
56,00 |
29,4 |
4,02 10-2 |
Wartość średnia wynosi: ![]()
29,17![]()
Odchylenie: ![]()
Przedział |
Liczba |
|
Rśr-3σ - Rśr-2σ |
28,29 - 28,59 |
5 |
Rśr-2σ - Rśr-σ |
28,59 - 28,87 |
17 |
Rśr-σ - Rśr |
28,87 - 29,17 |
12 |
Rśr - Rśr+σ |
29,17 - 29,47 |
58 |
Rśr+σ - Rśr+2σ |
29,47 - 29,77 |
8 |
Rśr+2σ - Rśr+3σ |
29,77 - 30,07 |
0 |
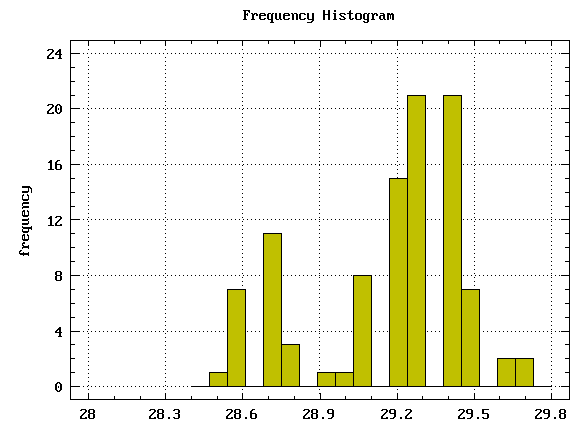
Porównanie z wartościami teoretycznymi dla rozkładu Gaussa.
Wartości teoretyczne dla punktów granicznych przedziałów obliczone ze wzoru:
R |
|
28,29 |
0,02 |
28,59 |
0,21 |
28,87 |
0,81 |
29,17 |
1,33 |
29,47 |
0,81 |
29,77 |
0,18 |
30,07 |
0,01 |
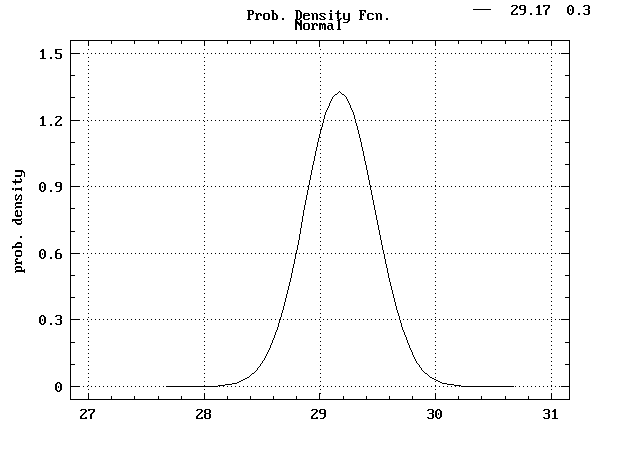
Rozkład krzywej Gaussa teoretyczny
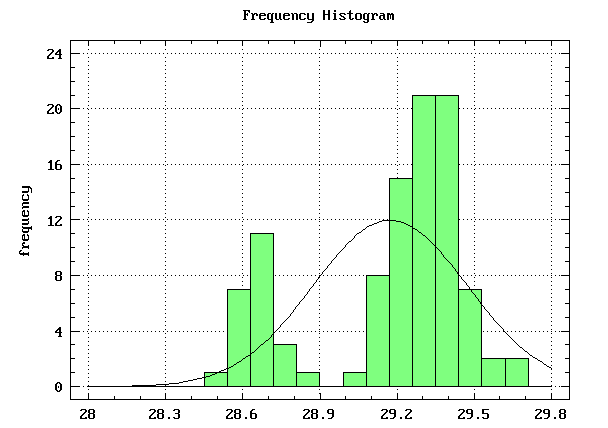
Rozkład otrzymany
Test ![]()
Do stwierdzenia zgodności otrzymanego doświadczalnie histogramu z krzywą Gaussa posługujemy testem ![]()
, zakładając poziom istotności ![]()
:
Stawiamy hipotezy:
Ho - rozkład uzyskany z doświadczenia jest rozkładem Gaussa
H1 - rozkład uzyskany z doświadczenia nie jest rozkładem
Gaussa
Chisquare Test
-----------------------------------------------------------------------
Lower Upper Observed Expected
Limit Limit Frequency Frequency Chisquare
-----------------------------------------------------------------------
at or below 28.720 19 6.5 23.914
28.720 28.864 3 8.6 3.637
28.864 28.936 1 6.3 4.486
28.936 29.008 1 7.6 5.778
29.008 29.080 0 8.7 8.725
29.080 29.152 8 9.4 0.208
29.152 29.224 15 9.6 0 3.099
29.224 29.296 0 9.2 9.176
29.296 29.368 21 8.3 19.343
29.368 29.440 21 7.1 27.084
29.440 29.512 7 5.7 0.272
29.512 29.656 2 7.5 4.073
above 29.656 2 5.3 2.087
-----------------------------------------------------------------------
Chisquare = 111.881 with 10 d.f. Sig. level = 0
Wynik testu pokazano w powyższej tabeli. Obliczona wartość ![]()
przy 10 stopniach swobody odpowiada poziomowi istotności ![]()
. Ponieważ jest on niższy niż założona wartość ![]()
, więc hipotezę o zgodności rozkładu należy odrzucić. IV. Wnioski
Zgodnie ze wstępem teoretycznym zostało potwierdzone twierdzenie że największy błąd popełniamy przy pomiarze długości a. Błędy rezystorów nastawnych i miliamperomierza są pomijalnie małe. przy pomiarach popełnialiśmy błędy systematyczne z:
błędu rezystorów dekadowych ( na zakresie do 10![]()
, na zakresie do 100![]()
)
wynikające z tego że miliamperomierz którego używaliśmy nie jest przyrządem idealnym i ma małą rezystancje wewnętrzną ( ![]()
)
z rezystancji źródła napięcia
oraz błąd przypadkowy przy odczycie długości a.
Pomiar połączeń szeregowych i równoległych ![]()
i ![]()
potwierdził z dużą dokładnością wzory teoretyczne. Po wykonaniu stu pomiarów ![]()
i analizie wyników stwierdziliśmy że rozkład wyników nie należy do rozkładu Gaussa, czyli rozkład popełnionych przez nas błędów przypadkowych nie jest opisany funkcją
Według tabeli rozdanej przez prowadzącego
Weryfikacja hipotez została przeprowadzona w programie STATGRAF
Według Jerzy Dąbrowski ”Statgraphics” str.136