Imię i nazwisko:	Ćwiczenie nr 15 Wyznaczanie ładunku właściwego elektronu e/m metodą magnetronową
Kierunek i rok: Fizyka Mag. Uzup. I	Ocena z kolokwium	Ocena ze sprawozdania	Ocena końcowa
Prowadzący ćwiczenia:

Część teoretyczna

Ruch cząsteczki naładowanej w polu magnetycznym i magnetycznym

Na elektron znajdujący się w polu elektrycznym i magnetycznym działa siła Lorentza

F = e(E + v x B)

Składa się ona z dwóch członów. Pierwszy pochodzi od działania pola elektrycznego o natężeniu E, a drugi od pola magnetycznego o indukcji B. Siła działająca na elektron w polu elektrycznym jest skierowana wzdłuż linii sił pola elektrycznego, a w polu magnetycznym prostopadle zarówno do kierunku linii sił indukcji magnetycznej B jak i do prędkości v. Na skutek działania siły Lorentza elektron w polu elektrycznym doznaje przyspieszenia. W lampach elektronowych istnieje zawsze pole elektryczne miedzy anodą i katodą. Pole elektryczne przyspieszające elektron wykonuje pracę określoną wzorem
,
. Praca ta zamienia się na energie kinetyczną elektronów
. Po przebyciu różnicy potencjałów
prędkość elektronów określona będzie równością pracy i energii kinetycznej
, skąd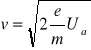

Działanie pól elektrycznych na cząsteczki naładowane można wykorzystać do dwóch podstawowych celów: 1) do przyspieszania lub hamowania, 2) do zmiany kierunku poruszających się cząsteczek. Oczywiście możliwe są takie układy gdzie obydwa te cele są realizowane jednocześnie.

Rysunek 1 przedstawia schemat układu, w którym występuje efekt magnetronowy. Podstawowym elementem jest dioda, której katodę stanowi cienki drucik znajdujący się w osi cylindrycznej anody. Cewka C służąca do wytwarzania indukcji magnetycznej znajduje się na zewnątrz diody.

Rys.1

Elektrony wybiegające z katody przyspieszane są w polu elektrycznym, którego linie sił biegną promieniście od anody A do katody K i równocześnie w polu o indukcji magnetycznej B skierowanej równolegle do osi lampy. W wyniku działania siły Lorentza, tor elektronu zakrzywia się w sposób pokazany na rys. 2

Rys.2

przedstawiającym zależność prądu anodowego od indukcji. Parametrem dla rodziny charakterystyk
jest napięcie anodowe
. Zjawisko wzrostu prądu uzyskać można zmieniając napięcie anodowe
przy stałej indukcji B. W tym przypadku prąd zaczyna płynąć przy pewnej krytycznej wartości napięcia wynoszącej
.

Dioda próżniowa

Najprostszy rodzaj lampy elektronowej. Posiada tylko dwie elektrody - anodę i katodę. Katoda jest źródłem elektronów, a anoda ich odbiorcą. Emisja z katody zachodzi pod wpływem wysokiej temperatury (termoemisja)- katoda jest żarzona najczęściej za pomocą prądu elektrycznego. Cechą charakterystyczną diody jest jednokierunkowy przepływ prądu elektrycznego: w kierunku od anody do katody (elektrony poruszają się w kierunku odwrotnym), w sytuacji, gdy anoda ma potencjał dodatni względem katody. W sytuacji przeciwnej lampa prądu nie przewodzi. Jednokierunkowe przewodzenie prądu zachodzi na skutek tego, że rozgrzana katoda emituje elektrony a zimna anoda nie emituje elektronów. Po wyemitowaniu przez katodę zostaną one przyciągnięte przez anodę, gdy ta ma potencjał dodatni; gdy anoda ma potencjał ujemny elektrony zostaną przez nią odepchnięte i wrócą do katody - przepływ prądu nie nastąpi.

Emisja elektronów

Próżnia jest doskonałym izolatorem. Jeżeli zatem dwa przeciwnie naładowane przewodniki umieścimy w próżni, w pewnej odległości od siebie, to prąd elektryczny nie popłynie. Prąd może płynąc wtedy, gdy istnieją elektrony. Wprawdzie w każdym z przewodników istnieją swobodne elektrony, lecz nie mogą one opuścić powierzchni. Elektron opuszczając powierzchnię przewodnika, musi wykonać pracę wyjścia równą różnicy energii elektronu w próżni i w metalu. Elektrony mogą zostać wyrwane z powierzchni przewodnika pod wpływem pewnych czynników zewnętrznych jak: silne pole elektryczne, wysoką temperaturę, oświetlenie jego powierzchni oraz bombardowanie powierzchni przez ine cząstki. Zgodnie z pasmową teorią metali elektron opuszczając metal musi wykonać pracę wyjścia Φ, która dla przeciętnego metalu jest rzędu Φ≈ 3 eV.

W zjawisku termoemisji energia potrzebna do wykonania pracy wyjścia jest dostarczona w postaci ciepła. Ilość emitowanych elektronów określamy gęstość prądu termoelektrycznego
. Zgodnie z prawem Richardsona-Dushmana
wyraża się następującym wzorem:

dla metali

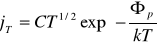
dla półprzewodników

T- temperatura ciała emitującego; k- stała Boltzmanna; Φ- praca wyjścia; A, C, b -wielkości stałe. W rzeczywistości obydwa wzory różnią się niewiele, ponieważ Φ>>kT i gęstość prądu jest określona przede wszystkim członem ekspotencjalnym, który w obydwu przypadkach ma taka sama postać. Prędkości termoelektronów nie są równe. Zależą one od rozkładu energii elektronów metalu w pobliżu poziomu Fermiego. W temperaturze 0
C obsadzone poziomy energetyczne są oddzielone poziomem Fermiego. W zjawisku termoelektrycznym emitują najszybsze elektrony, a więc te, których energia zawarta jest w przedziale E
do E
.

Część praktyczna

W tabeli I zostały przedstawione wyniki pomiarowe, które posłużą do wyznaczenia charakterystyki prądowo-napięciowej
diody przy indukcji cewki B = 0. Wyniki zostały uśrednione
[mA].

Tabela I

U [V]	I [mA]	I [mA]	I [mA]	I [mA]	I [mA]
1	0,7	0,6	0,6	0,6	0,6
2	1,9	1,6	1,7	1,5	1,7
3	2,8	2,3	2,5	2,1	2,4
4	3,3	2,7	3	2,5	2,9
5	3,5	3	3,2	2,7	3,1
6	3,6	3,2	3,3	2,9	3,2
7	3,7	3,5	3,3	3	3,4
8	3,7	3,6	3,4	3,1	3,4
9	3,9	3,8	3,4	3,2	3,6
10	4	3,9	3,5	3,4	3,7
11	4,1	4	3,6	3,4	3,8
12	4,1	4	3,6	3,5	3,8
13	4,2	4,1	3,7	3,6	3,9
14	4,2	4,2	3,7	3,7	3,9
15	4,3	4,2	3,8	3,7	4
16	4,3	4,3	3,8	3,8	4

Tabela II przedstawia wyniki, które posłużą do wyznaczenia charakterystyki zależności prądu anodowego w funkcji prądu zwojnicy
, z wykresu wyznaczę prąd krytyczny
.

Tabela II

I [mA]	U = 8 [V] I [mA]	U = 10 [V] I [mA]	U = 14 [V] I [mA]
2000	0,85	0,95	1,8
1900	0,95	1,05	2
1800	1,05	1,3	2,6
1700	1,35	1,7	2,8
1600	1,75	2,15	2,9
1500	2,15	2,35	3,2
1400	2,55	2,5	3,2
1300	2,8	2,7	3,3
1200	3,1	2,7	3,3
1100	2,8	2,75	3,4
1000	2,8	2,75	3,4
900	2,8	2,6	3,4
800	2,75	2,8	3,5
700	2,7	2,9	3,4
600	2,75	2,95	3,5
500	2,6	2,95	3,5
400	2,7	3	3,5
300	2,7	2,9	3,5
200	2,75	3	3,5
100	2,6	3	3,5
0	2,6	3	3,5

Wykorzystując wykres wyznaczam prąd krytyczny, następnie obliczam wartości indukcji krytycznych B
wykorzystując wzór:

=

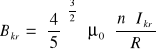
R= 5,5 10^-2 [m]

n= 320

Następnie oblicze wartość e/m korzystając z wzoru:

Wyniki obliczeni przedstawie w tabeli III

Tabela III

U [V]	[mA]	B [T]	e/m [C/kg]
8	1,85	0,0981	1,727 * 10
10	2	0,1046	1,670 * 10
14	2,8	0,1465	1,765 * 10

Wyznaczam średnią wartość e/m

[C/kg]

Wyznaczam odchylenia standardowego

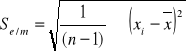
S_e/m = 0,047 * 10¹¹ [C/kg]

Obliczam błąd prawdopodobny metodą Studenta-Fishera. Poziom ufności przyjmuje

wartość
odczytuje z tablic

=0,82

Obliczam błąd maksymalny metodą Studenta-Fishera. Poziom ufności przyjmuje

wartość
odczytuje z tablic

=31,6

Wnioski

Celem doświadczenia było wyznaczenie ładunku właściwego elektronu e/m metodą magnetronową. Wynik jaki otrzymałem to e/m = 1,72 * 10
[C/kg], wartości tablicowe podają wynik
[C/kg], także widzimy że mój wynik nie różni się znacznie od wartości tablicowych. Podtwierdzają to także niskie wartości błędów prawdopodobnych i maksymalnych wyliczone metodą Studenta-Fishera.

Na wykresie przedstawiającym charakterystykę zależności prądu anodowego w funkcji prądu zwojnicy, widzimy że punkty pomiarowe dla U
= 8 [V] nie mieszczą się nawet w słupkach błędów i bardzo oddalone są od krzywej. Spowodowane jest to niestabilna pracą miernika, bądź faktem że zwojnica została dopiero podłączona pod napięcie i nie zdarzyła się ustabilizować. Wnioski takie wyciągnołem z faktu że już przy wartości napięcia 14 [V] oraz dłuższej pracy zwojnicy takie błędy grube nie występują.

---